Chapter 3 चतुर्भुजों को समझना
पाठान्तर्गत प्रश्नोत्तर
पाठ्य-पुस्तक पृष्ठ संख्या # 41
प्रश्न 1.
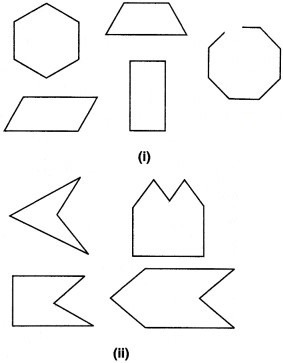
निम्न आकृतियों का सुमेलन कीजिए (ध्यान रखिए! एक आकृति का एक से अधिक आकृतियों से सुमेलन हो सकता है):
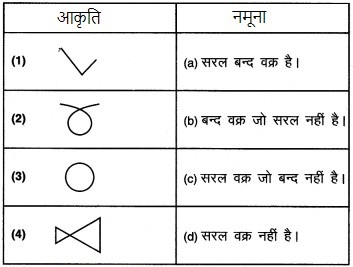
अपने मित्रों से इस मिलान की तुलना कीजिए। क्या वे सहमत हैं?
उत्तर:
- → (c)
- → (b)
- → (a)
- → (b)
हाँ, वे सहमत हैं।
पाठ्य-पुस्तक पृष्ठ संख्या # 42
प्रश्न 1.
कुछ और बहुभुजों के उदाहरण देने का प्रयास कीजिए तथा कुछ और ऐसे उदाहरण दीजिए जो बहुभुज न हों।
उत्तर:
(i) बहुभुज
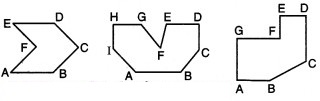
(ii) बहुभुज नहीं हैं –

प्रश्न 2.
एक बहुभुज की एक कच्ची (Rough) आकृति खींचिए और उसकी भुजाओं और शीर्षों की पहचान कीजिए।
हल:
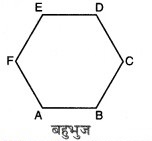
रेखाखण्ड जो बहुभुज बनाते हैं, बहुभुज की भुजाएँ कहलाती हैं तथा रेखाखण्ड परस्पर जहाँ मिलते हैं, बहुभुज के शीर्ष कहलाते हैं। संलग्न आकृति में, AB, BC, CD, DE, EF, तथा FA बहुभुज की भुजाएँ हैं तथा A, B, C, D, E और F शीर्ष हैं।
पाठ्य-पुस्तक पृष्ठ संख्या # 42-43
विकर्ण
प्रश्न 1.
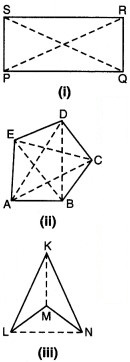
क्या आप संलग्न आकृतियों में प्रत्येक विकर्ण का नाम दे सकते हैं? क्या PQ एक विकर्ण है? LN के बारे में आप क्या कह सकते हैं?
हल:
किसी बहुभुज का विकर्ण उसके किन्हीं दो शीर्षों को जोड़ने से प्राप्त होता है।
चित्र (i) में, विकर्ण PR तथा QS हैं।
चित्र (ii) में, विकर्ण AC, AD, BD, BE और CE हैं।
चित्र (iii) में, विकर्ण KM और LN हैं। उत्तर
चित्र (i) में PQ विकर्ण नहीं है।
चित्र में (iii) LN विकर्ण है।
प्रश्न 2.
क्या बहिर्भाग की परिसीमा होती है?
उत्तर:
नहीं, बहिर्भाग की कोई परिसीमा नहीं होती है।
उत्तल और अवतल बहुभुज
प्रश्न 1.
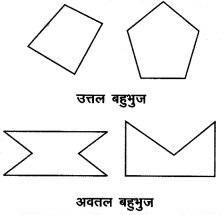
क्या आप बता सकते हैं कि इस प्रकार के बहुभुज एक-दूसरे से अलग क्यों हैं? जो बहुभुज उत्तल होते हैं उनके विकर्णों का कोई भी भाग बहिर्भाग में नहीं होता है। क्या यह अवतल बहुभुजों के लिए भी सत्य होता है? दी गई आकृतियों का अध्ययन कीजिए। तदुपरान्त अपने शब्दों में उत्तल बहुभुज तथा अवतल बहुभुज समझाने का प्रयास कीजिए। प्रत्येक प्रकार की दो आकृतियाँ बनाइए।
उत्तर:
इस प्रकार के बहुभुज एक-दूसरे से अलग इसलिए हैं क्योंकि इन बहुभुजों में कुछ उत्तल बहुभुज हैं ([आकृति (i)] तथा कुछ अवतल बहुभुज हैं [आकृति (ii)]। उत्तल बहुभुजों में उनके विकर्णों का कोई भाग बहिर्भाग में नहीं होता है। यह अवतल बहुभुजों के लिए सत्य नहीं हैं। उत्तल बहुभुज वे बहुभुज होते हैं जिनके शीर्ष बाहर की ओर होते हैं तथा उनके विकर्ण अभ्यंतर में होते हैं। अवतल बहुभुज के शीर्ष अन्दर की ओर होते हैं तथा उनके विकर्ण बहिर्भाग में हो सकते हैं।
सम तथा विषम बहुभुज
प्रश्न 1.
क्या एक आयत एक समबहुभुज है?
उत्तर:
नहीं, एक आयत एक समबहुभुज नहीं है। क्योंकि यह समकोणिक तो है परन्तु समभुज नहीं है।
प्रश्न 2.
क्या एक समबाहुत्रिभुज समबहुभुज है? क्यों?
उत्तर:
हाँ, एक समबाहु त्रिभुज समबहुभुज है। क्योंकि समबाहु त्रिभुज में भुजाएँ तथा कोण बराबर माप के होते हैं।
पाठ्य-पुस्तक पृष्ठ संख्या # 44
प्रश्न 1.
क्या आपने किसी ऐसे चतुर्भुज के बारे में पढ़ा है जो समभुज तो हो परन्तु समकोणिक न हो?
उत्तर:
हाँ, ऐसा चतुर्भुज सम चतुर्भुज है।
प्रश्न 2.
क्या कोई ऐसा त्रिभुज है जो समभुज तो हो परन्तु समकोणिक न हो?
उत्तर:
नहीं, ऐसा कोई त्रिभुज नहीं है।
पाठ्य-पुस्तक पृष्ठ संख्या # 44-45
इन्हें कीजिए
प्रश्न 1.
कोई एक चतुर्भुज, माना ABCD लीजिए (संलग्न चित्र 3.7)। एक विकर्ण खींचकर इसे दो त्रिभुजों में बाँटिए। आप छः कोण 1, 2, 3, 4, 5 और 6 प्राप्त करते हैं।
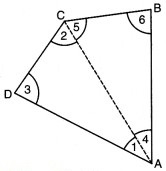
त्रिभुज के कोण-योग वाले गुणधर्म का उपयोग कीजिए और तर्क कीजिए कि कैसे ∠A, ∠B, ∠C तथा ZD के मापों का योगफल 180° + 180° = 360° हो जाता है।
हल:
माना कि ABCD एक चतुर्भुज है और AC इसका एक विकर्ण है।
स्पष्ट है कि
∠1 + ∠4 = ∠A
तथा ∠2 + ∠5 = ∠C
∴ त्रिभुज के तीनों कोणों के मापों का योग 180° होता है। अत: ∆ABC से,
∠4 + ∠5 + ∠B = 180° …..(1)
∆ACD से,
∠1 + ∠2 + ∠D = 180° …..(2)
समीकरण (1) व (2) को जोड़ने पर, हम प्राप्त करते हैं।
∠4 + ∠5 + ∠B + ∠1 + ∠2 + ∠D = 180° + 180°
या (∠1 + ∠4) + ∠B + (∠2 + ∠5) + ∠D = 360°
या ∠A+ ∠B + ∠C+ ∠D = 360°
अतः ∠A+ ∠B + ∠C+ ∠D = 360°
प्रश्न 2.
किसी चतुर्भुज ABCD, की गत्ते वाली चार सर्वांगसम प्रतिलिपियाँ लीजिए जिनके कोण दर्शाए गए हैं। [आकृति 3.8 (i)]। इन प्रतिलिपियों को इस प्रकार से व्यवस्थित कीजिए जिसमें ∠1, ∠2, ∠3, ∠4 एक ही बिन्दु पर मिलें जैसा कि आकृति 3.8 (ii) में है।
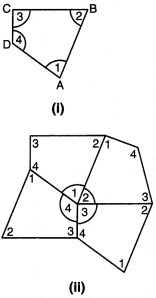
आप ∠1, ∠2, ∠3 तथा ∠4 के योगफल के बारे में क्या कह सकते हैं?
हल:
किसी चतुर्भुज ABCD के लिए,
m∠1 + m∠2 + m∠3 + m∠4 = 360°
अतः एक चतुर्भुज के चारों कोणों के मापों का योगफल 360° होता है।
प्रश्न 3.
चतुर्भुज ABCD पर पुनः विचार कीजिए (चित्र 3.9)। माना इसके अभ्यंतर में कोई बिन्दु P स्थित है। P को शीर्षों A, B, C तथा D से जोड़िए। आकृति में ∆PAB पर विचार कीजिए। हम देखते हैं कि x=180° – m∠2 – m∠3 ; इसी प्रकार APBC, से y = 180° – m∠4 – m∠5;
∆PCD से z = 180° – m∠6 – m∠7; और
∆PDA से w = 180° – m∠8 – m∠1.
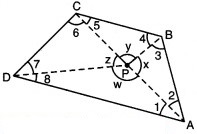
इसका उपयोग करके कुल माप m∠1 + m∠2 + …… + m∠8 ज्ञात कीजिए। क्या यह आपको परिणाम तक पहुँचाने में सहायता करता है? याद रखिए ∠x + ∠y + ∠z + ∠w = 360° है।
हल:
क्योंकि त्रिभुज के तीनों कोणों के मापों का योग 180° होता है;
अतः x = 180° – m∠2 – m∠3 …… (1)
y = 180° – m∠4 – m∠5 ….. (2)
z = 180° – m∠6 – m∠7 …… (3)
w = 180° – m∠8 – m∠1 …… (4)
समीकरण (1), (2), (3) एवं (4) को जोड़ने पर, हम प्राप्त करते हैं –
x + y + z + w = 720° – ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8
लेकिन x + y + z +w = 360°
360° = 720° – ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7+ ∠8
= 720° – (∠A + ∠B + ∠C + ∠D)
या ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 720° – 360° = 360°
हाँ, यह हमें सहायता करता है कि चतुर्भुज के कोणों के मापों का योग 360° होता है।
प्रश्न 4.
ये सभी चतुर्भुज उत्तल (convex) चतुर्भुज थे। यदि चतुर्भुज उत्तल नहीं होते तो क्या होता ? चतुर्भुज ABCD पर विचार कीजिए।
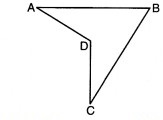
इसे दो त्रिभुजों में बाँटिए और अन्तःकोणों का योगफल ज्ञात कीजिए (चित्र : 3.10)।
हल:
चतुर्भुज ABCD के विकर्ण BD को मिलाया।
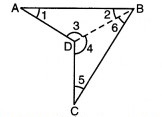
त्रिभुज के कोण-योग गुणधर्म से,
∆ABD से, m∠1 + m∠2 + m∠3 = 180° …(1)
∆BCD से, m∠4 + m∠5 + m∠6 = 180° …(2)
समीकरण (1) व (2) को जोड़ने पर,
m∠1 + m∠2 + m∠3 + m∠4 + m∠5 + m∠6 = 180° + 180°
या m∠1 + (m∠2 + m∠6) + m∠5 + m∠3 + m∠4 = 360°
या ∠A + ∠B + ∠C + ∠D = 360°
अतः चतुर्भुज के अन्त:कोणों का योग = 360°