Chapter 4 प्रायोगिक ज्यामिती

Chapter 4 प्रायोगिक ज्यामिती

पाठान्तर्गत प्रश्नोत्तर

पाठ्य-पुस्तक पृष्ठ संख्या # 64

इन्हें कीजिए

प्रश्न 1.
क्या एक अद्वितीय चतुर्भुज की रचना के लिए कोई भी पाँच माप (भुजाओं और कोणों की) पर्याप्त हैं?
उत्तर:
हाँ, किसी भी अद्वितीय चतुर्भुज की रचना के लिए कोई भी पाँच माप पर्याप्त हो सकती हैं।

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 4.1) –

प्रश्न 1.
अरशद के पास एक चतुर्भुज ABCD की पाँच माप हैं। ये माप AB = 5 cm, ∠A = 50°, AC = 4 cm, BD = 5 cm और AD = 6 cm हैं। क्या वह इन मापों से एक अद्वितीय चतुर्भुज बना सकता है? अपने उत्तर के कारण दीजिए।
उत्तर:
दी गई मापों से चतुर्भुज ABCD नहीं बन सकता है। कारण निम्न हैं –

1. विकर्ण AC =4 cm लेने पर ∆ABC की रचना सम्भव है परन्तु ∆ACD की रचना सम्भव नहीं है। अतः चतुर्भुज ABCD नहीं बन सकता है।
2. विकर्ण BD = 5 cm लेने पर AABD एवं ABCD सम्भव नहीं है। अतः चतुर्भुज ABCD बनना असम्भव है।

पाठ्य-पुस्तक पृष्ठ संख्या # 66

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 4.2) –

प्रश्न 1.
हमने देखा कि एक चतुर्भुज की पाँच मापों से एक अद्वितीय चतुर्भुज की रचना की जा सकती है। क्या आप सोचते हैं कि चतुर्भुज की किन्हीं पाँच मापों से ऐसी रचना की जा सकती है?
उत्तर:
हाँ, एक अद्वितीय चतुर्भुज की रचना करने के लिए पाँच मापों का होना आवश्यक है। परन्तु इन मापों का अद्वितीय होना भी आवश्यक है। अद्वितीय चतुर्भुज की रचना के लिए निम्न मापों का होना आवश्यक है –

1. चारों भुजाएँ और एक विकर्ण।
2. दो विकर्ण और तीन भुजाएँ।
3. दो आसन्न भुजाएँ और तीन कोण।
4. तीन भुजाएँ और उनके बीच के दो कोण।
5. अन्य विशिष्ट गुण।

प्रश्न 2.
क्या आप एक समान्तर चतुर्भुज BATS की रचना कर सकते हैं जिसमें BA = 5 cm, AT = 6 cm और AS = 6.5 cm हो? क्यों?
उत्तर:
हाँ, इन मापों से समान्तर चतुर्भुज BATS की रचना की जा सकती है। इन मापों से ∆BAS और ∆SAT की रचना करके समान्तर चतुर्भुज BATS की रचना की जा सकती है।

प्रश्न 3.
क्या आप एक समचतुर्भुज (Rhombus) ZEAL की रचना कर सकते हैं जिसमें ZE = 3.5 cm विकर्ण EL= 5 cm है ? क्यों ?
उत्तर:
हाँ, दी गई मापों से सम-चतुर्भुज ZEAL की रचना कर सकते हैं। समचतुर्भुज की रचना ∆ZEL तथा ∆LEA की रचना करके की जा सकती है।

प्रश्न 4.
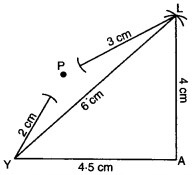
एक विद्यार्थी चतुर्भुज PLAY की रचना करने का प्रयास करता है जिसमें PL = 3 cm, LA = 4 cm, AY = 4.5 cm, PY = 2 cm और LY = 6 cm है, परन्तु वह इसकी रचना नहीं कर सका। कारण बताइए।
हल:
चतुर्भुज PLAY की रचना करने के लिए इसे दो त्रिभुजों ∆PLY तथा ∆LAY में विभाजित किया। दी हुई मापों से ∆LAY की रचना की। ∆PLY की रचना दी गई मापों से असम्भव है, क्योंकि PL + PY < LY अर्थात् 3 + 2 < 6 अतः ∆PLY की रचना सम्भव नहीं है। अत: चतुर्भुज PLAY को दो त्रिभुजों में विभाजित नहीं किया जा सकता। इसलिए चतुर्भुज PLAY की रचना नहीं की जा सकती है।