Chapter 4 प्रायोगिक ज्यामिती Ex 4.5
निम्नलिखित की रचना कीजिए –
प्रश्न 1.
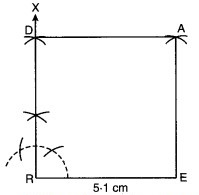
एक वर्ग READ जिसमें RE = 5.1 cm है।
हल:
रचना के चरण –
- एक सर्वप्रथम एक रेखाखण्ड RE = 5.1 cm बनाया।
- रेखाखण्ड RE के R के बिन्दु पर ∠XRE = 90° बनाया।
- किरण RX से 5.1 cm लम्बा रेखाखण्ड काट लिया।
- D तथा E बिन्दुओं के केन्द्र मानकर और 4 cm त्रिज्या लेकर दो चाप लगाए जो एक-दूसरे को A पर काटते हैं।
- DA तथा EA को मिलाया। इस प्रकार प्राप्त आकृति READ अभीष्ट वर्ग है।
प्रश्न 2.
एक समचतुर्भुज जिनके विकर्णों की लम्बाई 5.2 cm और 6-4 cm है।
हल:
रचना के चरण –
- माना कि विकर्ण AC = 5.2 cm तथा BD = 6.4 cm है।
- रेखाखण्ड AC = 5.2 cm बनाया।
-
AC का लम्ब समद्विभाजक खींचा जो AC को O बिन्दु पर काटता है।

- O बिन्दु को केन्द्र मानकर तथा = cm = 3.2 cm त्रिज्या लेकर दो चाप लगाए जो OX को D पर तथा OY को B पर काटता है।
- AD, CD, CB और AB को मिलाया।
- प्राप्त आकृति ABCD अभीष्ट समचतुर्भुज है।
प्रश्न 3.
एक आयत जिसकी आसन्न भुजाओं की लम्बाइयाँ 5 cm और 4 cm हैं।
हल:
रचना के चरण –
- सर्वप्रथम रेखाखण्ड PQ = 5 cm बनाया।
- P बिन्दु पर ZQPX = 90° बनाया।
- बिन्दु K को केन्द्र मानकर तथा 4 cm त्रिज्या लेकर चाप लगाया जो XP सेवा को S पर प्रतिच्छेद करता है।
- अब S को केन्द्र मानकर तथा 5 cm त्रिज्या लेकर एक चाप लगाया।
- Q बिन्दु को केन्द्र मानकर तथा 4 cm त्रिज्या लेकर एक चाप लगाया। ये दोनों चाप एक दूसरे को बिन्दु R पर प्रतिच्छेद करते हैं।
- SR तथा QR को मिलाया। इस प्रकार प्राप्त आकृति PQRS एक अभीष्ट आयत है।

प्रश्न 4.
एक समान्तर चतुर्भुज OKAY जहाँ OK = 5.5 cm और KA = 4.2 cm है। क्या यह अद्वितीय है?
हल:
किसी चतुर्भुज की रचना के लिए पाँच मापों का होना आवश्यक है।
यहाँ समान्तर चतुर्भुज की रचना के लिए दो आसन्न भुजाएँ दी गई हैं। अर्थात् चार भुजाएँ दी गई हैं। सम्मुख भुजाएँ बराबर हैं। अतः चतुर्भुज की रचना के लिए एक और माप आवश्यक है। यह माप दो आसन्न भुजाओं के बीच का कोण हो सकता है या अद्वितीय चतुर्भुज के लिए यह एक विकर्ण हो सकता है।
अतः दी गई चार मापों से अभीष्ट समान्तर चतुर्भुज की रचना नहीं हो सकती है।