Chapter 4 द्विघात समीकरण Ex 4.3
प्रश्न 1.
यदि निम्नलिखित द्विघात समीकरणों के मूलों का अस्तित्व हो, तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए :
(i) 2x2 – 7x + 3 = 0
हल-
प्रश्नानुसार द्विघात समीकरण है-
2x2 – 7x + 3 = 0
या 2x2 – 7x = -3
(चूँकि पूर्ण वर्ग बनाने के लिए x2 का गुणांक इकाई होना चाहिये)
पूर्ण वर्ग बनाने के लिए दोनों पक्षों में x के गुणांक के आधे का वर्ग जोड़ते हैं।




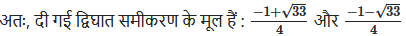
(iii) 4x2 + 4√3x + 3 = 0
हल-
प्रश्नानुसार द्विघात समीकरण है
4x2 + 4√3x + 3 = 0
या 4x2 + 4√3x = -3
![]()
(x2 का गुणांक इकाई बनाने पर)

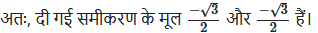
(iv) 2x2 + x + 4 = 0
हल-
प्रश्नानुसार द्विघात समीकरण है-
2x2 + x + 4 = 0
या 2x2 + x = -4
![]()
(x2 का गुणांक इकाई बनाने पर)
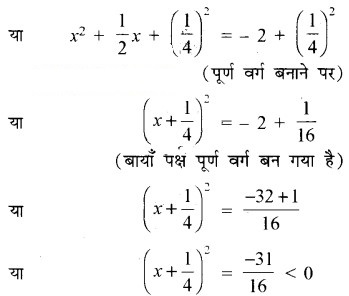
∵ किसी संख्या का वर्ग ऋणात्मक नहीं हो सकता।

∴ यहाँ x का कोई भी वास्तविक मान नहीं है जो दी गई द्विघात समीकरण को सन्तुष्ट करता हो।
अतः, दिए गए समीकरण के कोई वास्तविक मूल नहीं हैं।
अतः समीकरण के मूलों का अस्तित्व नहीं है।
प्रश्न 2.
उपर्युक्त प्रश्न 1 में दिए गए द्विघात समीकरणों के मूल, द्विघाती सूत्र का उपयोग करके ज्ञात कीजिए।
(i) 2x2 – 7x + 3 = 0
हल-
प्रश्नानुसार द्विघात समीकरण है-
2x2 – 7x + 3 = 0
इसकी ax2 + bx + c = 0 से तुलना करने पर,
∴ a = 2, b = -7, c = 3
अब b2 – 4ac = (-7)2 – 4 × 2 × 3
= 49 – 24
= 25 > 0
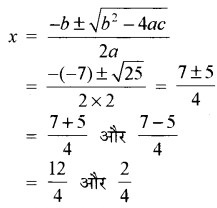
= 3 और 1/2
अतः, 3 और 1/2 दी गई द्विघात समीकरण के मूल हैं।
(ii) 2x2 + x – 4 = 0
हल-
प्रश्नानुसार द्विघात समीकरण है-
2x2 + x – 4 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = 1, c = -4
अब, b2 – 4ac = (1)2 – 4 × 2 × (-4)
= 1 + 32
= 33 > 0
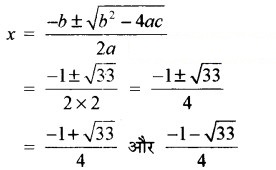
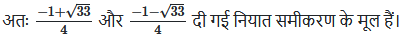
(iii) 4x2 + 4√3x + 3 = 0
हल-
प्रश्नानुसार द्विघात समीकरण है-
4x2 + 4√3x + 3 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 4, b = 4√3, c = 3
अब, b2 – 4ac = (4√3)2 – 4 × 4 × 3
= 48 – 48
= 0
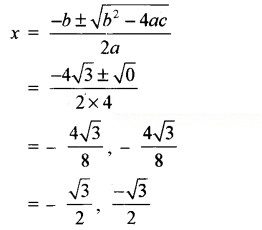
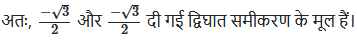
(iv) 2x2 + x + 4 = 0
हल-
प्रश्नानुसार द्विघात समीकरण है-
2x2 + x + 4 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 2, b = 1, c = 4
अब, b2 – 4ac = (1)2 – 4 × 2 × 4
= 1 – 32
= -31 < 0
![]()
क्योंकि एक वास्तविक संख्या का वर्ग ऋणात्मक नहीं हो सकता। इसलिए x का कोई वास्तविक मान नहीं होगा।
अतः दिए गए समीकरण के कोई वास्तविक मूल नहीं हैं।
अतः समीकरण के मूलों का अस्तित्व नहीं है।
प्रश्न 3.
निम्न समीकरणों के मूल ज्ञात कीजिए-
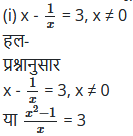
या x2 – 1 = 3x
या x2 – 3x – 1 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = -3, c = -1
अब, b2 – 4ac = (-3)2 – 4 × 1 × (-1)
= 9 + 4
= 13 > 0
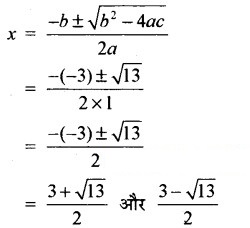

हल-
प्रश्नानुसार
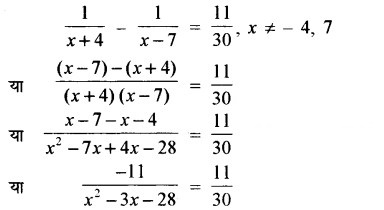
या -11 × 30 = 11(x2 – 3x – 28)
या -30 = x2 – 3x – 28
या x2 – 3x – 28 + 30 = 0
या x2 – 3x + 2 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = -3, c = 2
अब, b2 – 4ac = (-3)2 – 4 × 1 × 2
= 9 – 8
= 1 > 0
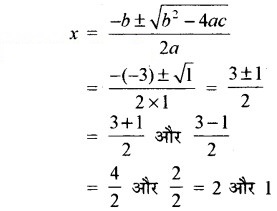
अतः, 2 और 1 दी गई द्विघात समीकरण के मूल हैं।
प्रश्न 4.
3 वर्ष पूर्व रहमान की आयु (वर्षों में) का व्युत्क्रम और अब से 5 वर्ष पश्चात् आयु के व्युत्क्रम का योग 1/3 है। उसकी वर्तमान आयु ज्ञात कीजिए।
हल-
माना कि रहमान की वर्तमान आयु = x वर्ष
3 वर्ष पूर्व रहमान की आयु= (x – 3) वर्ष
अब से 5 वर्ष पश्चात् रहमान की आयु = (x + 5) वर्ष
प्रश्नानुसार
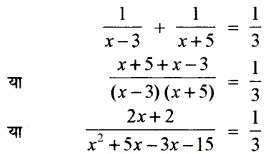
![]()
या 6x + 6 = x2 + 2x – 15
या x2 + 2x – 15 – 6x – 6 = 0
या x2 – 4x – 21 = 0, जो कि x में द्विघात है।
इसलिए इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = -4, c = -21
अब, b2 – 4ac = (-4)2 – 4 × 1 × (-21)
= 16 + 84
= 100 > 0
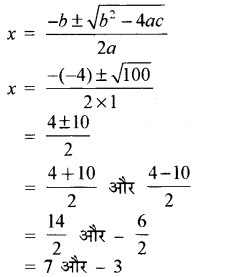
∵ आयु ऋणात्मक नहीं हो सकती।
इसलिए x = -3 को छोड़ने पर
∴ x = 7
अतः, रहमान की वर्तमान आयु = 7 वर्ष।
प्रश्न 5.
एक क्लास टेस्ट में शेफाली के गणित और अंग्रेजी में प्राप्त किए गए अंकों का योग 30 है। यदि उसको गणित में 2 अंक अधिक और अंग्रेजी में 3 अंक कम मिले होते, तो उनके अंकों का गुणनफल 210 होता। उसके द्वारा दोनों विषयों में प्राप्त किए अंक ज्ञात कीजिए।
हल-
माना कि शेफाली के गणित में प्राप्त अंक = x
शेफाली के अंग्रेजी में अंक = 30 – x
पहली शर्त के अनुसार
शेफाली के गणित में अंक = x + 2
और शेफाली के अंग्रेजी में अंक = 30 – x – 3 = 27 – x
∴ उनका गुणनफल = (x + 2) (27 – x)
= 27x – x2 + 54 – 2x
= -x2 + 25x + 54
प्रश्न की दूसरी शर्त के अनुसार,
-x2 + 25x + 54 = 210
या -x2 + 25x + 54 – 210 = 0
या -x2 + 25x – 156 = 0
या x2 – 25x + 156 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = -25, c = 156
अब, b2 – 4ac = (-25)2 – 4 × 1 × 156
= 625 – 624
= 1 > 0
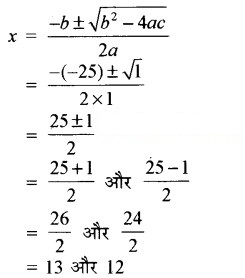
स्थिति I.
जब x = 13
तब शेफाली के गणित में अंक = 13
शेफाली के अंग्रेजी में अंक = 30 – 13 = 17
स्थिति II.
जब x = 12
तब शेफाली के गणित में अंक = 12
शेफाली के अंग्रेजी में अंक = 30 – 12 = 18
अतः, शेफाली के दो विषयों में अंक हैं : 13 और 17 या 12 और 18
प्रश्न 6.
एक आयताकार खेत का विकर्ण उसकी छोटी भुजा से 60 मीटर अधिक लम्बा है। यदि बड़ी भुजा छोटी भुजा से 30 मीटर अधिक हो, तो खेत की भुजाएँ ज्ञात कीजिए।
हल-
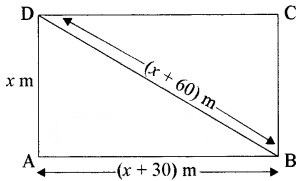
माना कि आयताकार खेत की छोटी भुजा = AD = x m
आयताकार खेत की लम्बी भुजा = AB = (x + 30) m
और आयताकार खेत का विकर्ण = DB = (x + 60) m
एक आयत में लम्बाई और चौड़ाई के बीच का कोण समकोण होता है।
∴ ∠DAB = 90°
अब समकोण त्रिभुज DAB में, पाइथागोरस प्रमेय से-
(DB)2 = (AD)2 + (AB)2
या (x + 60)2 = (x)2 + (x + 30)2
या x2 + 3600 + 120x = x2 + x2 + 900 + 60x
या x2 + 3600 + 120x – 2x2 – 900 – 60x = 0
या -x2 + 60x + 2700 = 0
या x2 – 60x – 2700 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = -60, c = -2700
और b2 – 4ac = (-60)2 – 4 × 1 × (-2700)
= 3600 + 10800
= 14400 > 0
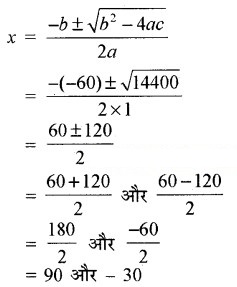
∵ किसी भी भुजा की लम्बाई ऋणात्मक नहीं होती।
इसलिए x = -30 को छोड़ने पर
∴ x = 90
अतः आयताकार खेत की सबसे छोटी भुजा = 90 m
आयताकार खेत की लम्बी भुजा = (90 + 30) m = 120 m
प्रश्न 7.
दो संख्याओं के वर्गों का अन्तर 180 है। छोटी संख्या का वर्ग बड़ी संख्या का आठ गुना है। दोनों संख्याएँ ज्ञात कीजिए।
हल-
माना कि बड़ी संख्या = x
छोटी संख्या = y
प्रश्न की पहली शर्त के अनुसार,
x2 – y2 = 180 ……(1)
प्रश्न की दूसरी शर्त के अनुसार,
y2 = 8x ……(2)
(1) और (2) से
x2 – 8x = 180
या x2 – 8x – 180 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = -8, c = -180
और b2 – 4ac = (-8)2 – 4 × 1 × (-180)
= 64 + 720
= 784 > 0
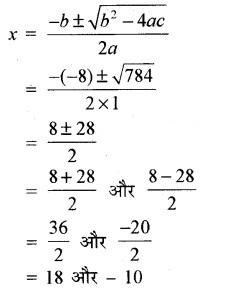
जब x = -10 तो, (2) से y2 = 8(-10) = -80, जो कि सम्भव नहीं है।
इसलिए x = -10 को छोड़ने पर
जब x = 18, तो (2) से,
y2 = 8(18) = 144
या y = ±√144
y = ±12
अतः अभीष्ट संख्याएँ 18 और 12 या 18 और -12 है।
प्रश्न 8.
एक रेलगाड़ी एक समान चाल से 360 km दूरी तय करती है। यदि यह चाल 5 km/h अधिक होती, तो वह उसी यात्रा में 1 घण्टा कम समय लेती। रेलगाड़ी की चाल ज्ञात कीजिए।
हल-

या 1800 = x2 + 5x
या x2 + 5x – 1800 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = 5, c = -1800
और b2 – 4ac = (5)2 – 4 × 1 × (-1800)
= 25 + 7200
= 7225 > 0
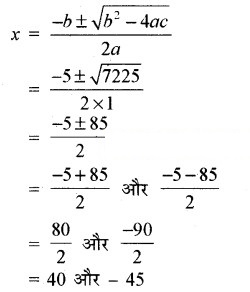
∴ किसी रेलगाड़ी की चाल ऋणात्मक नहीं हो सकती।
इसलिए x = -45 को छोड़ने पर
∴ x = 40
अतः रेलगाड़ी की चाल = 40 km/hour
प्रश्न 9.

हल-
मान लीजिए बड़े व्यास वाले नल द्वारा हौज को भरने में लिया गया समय = x घण्टे
छोटे नल द्वारा हौज भरने में लिया गया समय = (x + 10) घण्टे
एक घण्टे की स्थिति में,

समीकरण (1) और (2) से

या 75(2x + 10) = 8(x2 + 10x)
या 150x + 750 = 8x2 + 80x
या 8x2 + 80x – 150x – 750 = 0
या 8x2 – 70x – 750 = 0
या 4x2 – 35x – 375 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 4, b = -35, c = -375
और b2 – 4ac = (-35)2 – 4 × 4 × (-375)
= 1225 + 6000
= 7225 > 0
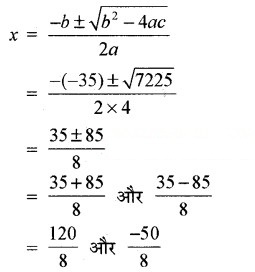

∴ x = 15
अतः बड़े नल द्वारा हौज भरने का समय = 15 घण्टे
और छोटे नल द्वारा हौज भरने का समय = (15 + 10) घण्टे = 25 घण्टे
प्रश्न 10.
मैसूर और बैंगलोर के बीच के 132 km यात्रा करने में एक एक्सप्रेस रेलगाड़ी, सवारी गाड़ी से 1 घण्टा समय कम लेती है (मध्य के स्टेशनों पर ठहरने का समय ध्यान में न लिया जाए)। यदि एक्सप्रेस रेलगाड़ी की औसत चाल, सवारी गाड़ी की औसत चाल से 11 km/h अधिक हो, तो दोनों रेलगाड़ियों की औसत चाल ज्ञात कीजिए।
हल-
माना कि
सवारी गाड़ी की औसत चाल = x km/hour
एक्सप्रेस रेलगाड़ी की औसत चाल = (x + 11) km/hour
मैसूर और बैंगलोर के बीच की दूरी = 132 km

या 1452 = x2 + 11x
या x2 + 11x – 1452 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = 11, c = -1452
और b2 – 4ac = (11)2 – 4 × 1 × (-1452)
= 121 + 5808
= 5929 > 0
![]()
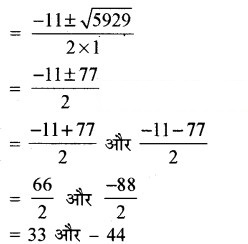
∵ रेलगाड़ी की चाल ऋणात्मक नहीं हो सकती
∴ x = 33
अतः, सवारी गाड़ी की औसत चाल = 33 km/hour
और एक्सप्रेस रेलगाड़ी की औसत चाल = (33 + 11) km/hour = 44 km/hour
प्रश्न 11.
दो वर्गों के क्षेत्रफलों का योग 468 m2 है। यदि उनके परिमापों का अन्तर 24 m हो, तो दोनों वर्गों की भुजाएँ ज्ञात कीजिए।
हल-
पहले बड़े वर्ग की स्थिति में
माना कि वर्ग की प्रत्येक भुजा की लम्बाई = x m
वर्ग का क्षेत्रफल = x2 m2
वर्ग का परिमाप = 4x m
छोटे वर्ग की स्थिति में
माना किवर्ग की प्रत्येक भुजा की लम्बाई = y m
वर्ग का क्षेत्रफल = y2 m2
वर्ग का परिमाप = 4y m
पहली शर्त के अनुसार,
x2 + y2 = 468 ……(1)
दूसरी शर्त के अनुसार,
4x – 4y = 24
या 4(x – y) = 24
या x – y = 6
या x = 6 + y ……(2)
(1) और (2) से,
(6 + y)2 + y2 = 468
या 36 + y2 + 12y + y2 = 468
या 2y2 + 12y + 36 – 468 = 0
या 2y2 + 12y – 432 = 0
या y2 + 6y – 216 = 0
इसकी तुलना ay2 + by + c = 0 से करने पर,
∴ a = 1, b = 6, c = -216
और b2 – 4ac = (6)2 – 4 × 1 × (-216)
= 36 + 864
= 900 > 0
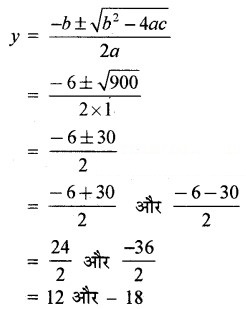
∵ वर्ग की भुजा की लम्बाई ऋणात्मक नहीं हो सकती।
इसलिए. y = -18 को छोड़ने पर
∴ y = 12
(2) से, x = 6 + 12 = 18
अतः, दो वर्गों की भुजाएँ 12 m और 18 m हैं।