Chapter 4 Lines and Angles Ex 4.2
Question 1.
In figure, find the values of x and y and then show that AB || CD.
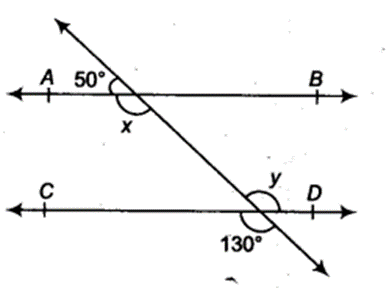
Solution:
∵ x + 50° = 180° (Linear pair)
⇒ x = 130°
∴ y = 130° (Vertically opposite angle)
Here, ∠x = ∠COD = 130°
These are corresponding angles for lines AB and CD.
Hence, AB || CD
Question 2.
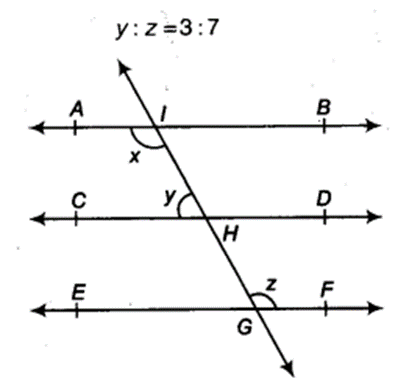
In figure, if AB || CD, CD || EF and y: z = 3:7, find x.
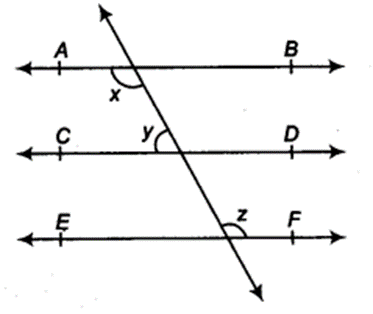
Solution:
Given

Question 3.
In figure, if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
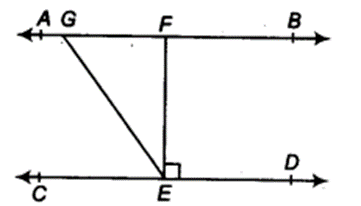
Solution:
∵ ∠AGE = ∠GED (Alternate interior angles)
But ∠GED = 126°
⇒ ∠AGE = 126° ….(i)
∴ ∠GEF + ∠FED= 126°
⇒ ∠GEF + 90° =126° (∵ EF ⊥ CD)
⇒ ∠GEF = 36°
Also, ∠AGE + ∠FGE = 180° (Linear pair axiom)
⇒ 126° + ∠FGE =180°
⇒ ∠FGE = 54°
Question 4.
In figure, if PQ || ST, ∠ PQR = 110° and ∠ RST = 130°, find ∠QRS.
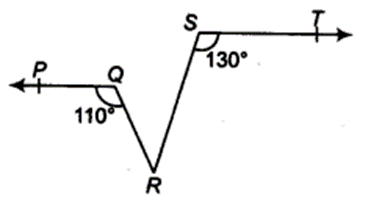
Solution:
Drawing a tine parallel to ST through R.

Question 5.
In figure, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.
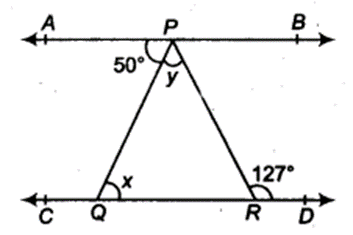
Solution:
We have, AB || CD
⇒ ∠APQ = ∠PQR (Alternate interior angles)
⇒ 50° = x
⇒ x = 50°
Now, ∠PQR + ∠QPR = 127°
(Exterior angle is equal to sum of interior opposite angles of a triangle)
⇒ 50°+ ∠QPR = 127°
⇒ y = 77°.
Question 6.
In figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
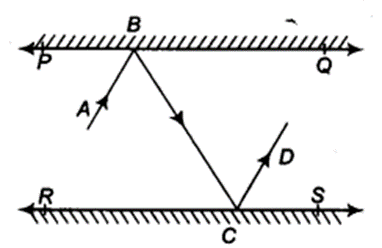
Solution:
