Chapter 4 Simple Equations
Very Short Answer Type
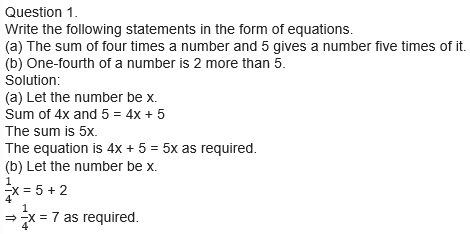
Question 2.
Convert the following equations in statement form:
(a) 5x = 20
(b) 3y + 7 = 1
Solution:
(a) Five times a number x gives 20.
(b) Add 7 to three times a number y gives 1.
Question 3.
If k + 7 = 10, find the value of 9k – 50.
Solution:
k + 7 = 10
⇒ k = 10 – 7 = 3
Put k = 3 in 9k – 50, we get
9 × 3 – 50 = 27 – 50 = -23
Thus the value of k = -23
Question 4.
Solve the following equations and check the answers.
![]()
Solution:


Question 5.
Solve the following equations:
3(y – 2) = 2(y – 1) – 3
Solution:
3(y – 2) = 2(y – 1) – 3
⇒ 3y – 6 = 2y – 2 – 3 (Removing the brackets)
⇒ 3y – 6 = 2y – 5
⇒ 3y – 2y = 6 – 5 (Transposing 6 to RHS and 2y to LHS)
⇒ y = 1
Thus y = 1
Question 6.
If 5 is added to twice a number, the result is 29. Find the number.
Solution:
Let the required number be x.
Step I: 2x + 5
Step II: 2x + 5 = 29
Solving the equation, we get
2x + 5 = 29
⇒ 2x = 29 – 5 (Transposing 5 to RHS)
⇒ 2x = 24
⇒ x = 12 (Dividing both sides by 2)
⇒ x = 12
Thus the required number is 12.
Question 7.
If one-third of a number exceeds its one-fourth by 1, find the number.
Solution:
Let the required number be x.

Short Answer Type
Question 8.
The length of a rectangle is twice its breadth. If its perimeter is 60 cm, find the length and the breadth of the rectangle.
Solution:
Let the breadth of the rectangle be x cm.
its length = 2x
Perimeter = 2 (length + breadth) = 2(2x + x) = 2 × 3x = 6x
As per the condition of the question, we have
6x = 60 ⇒ x = 10
Thus the required breadth = 10 cm
and the length = 10 × 2 = 20 cm.
Question 9.
Seven times a number is 12 less than thirteen times the same number. Find the number.
Solution:
Let the required number be x.
7x = 13x – 12
⇒ 7x – 13x = -12 (Transposing 13x to LHS)
⇒ -6x = -12
⇒ x = 2
Thus, the required number is 2.


Question 11.
The sum of three consecutive multiples of 2 is 18. Find the numbers.
Solution:
Let the three consecutive multiples of 2 be 2x, 2x + 2 and 2x + 4.
As per the conditions of the question, we have
2x + (2x + 2) + (2x + 4) = 18
⇒ 2x + 2x + 2 + 2x + 4 = 18
⇒ 6x + 6 = 18
⇒ 6x = 18 – 6 (Transposing 6 to RHS)
⇒ 6x = 12
⇒ x = 2
Thus, the required multiples are
2 × 2 = 4, 4 + 2 = 6, 6 + 2 = 8 i.e., 4, 6 and 8.
Question 12.
Each of the 2 equal sides of an isosceles triangle is twice as large as the third side. If the perimeter of the triangle is 30 cm, find the length of each side of the triangle. [NCERT Exemplar]
Solution:
Let the length of the third side be x cm.
Each equal side = 2x cm.
As per the condition of the question, we have
Perimeter = x + 2x + 2x = 30
⇒ 5x = 30
⇒ x = 6
Thus, the third side of the triangle = 6 cm
and other two equal sides are 2 × 6 = 12 cm each


Thus, the required journey = 180 km.