Chapter 5 प्रारंभिक आकारों को समझना Ex 5.6
पाठ्य-पुस्तक पृष्ठ संख्या # 113-114
प्रश्न 1.
निम्नलिखित त्रिभुजों के प्रकार लिखिए :
(a) त्रिभुज जिसकी भुजाएँ 7 सेमी, 8 सेमी और 9 सेमी हैं।
(b) ∆ABC जिसमें AB = 8.7 सेमी, AC = 7 सेमी और BC = 6 सेमी है।
(c) ∆PQR जिसमें PQ = QR = RP = 5 सेमी है।
(d) ∆DEF जिसमें m∠D = 90° ।
(e) ∆XYZ जिसमें m∠Y = 90° और XY = YZ है।
(f) ∆LMN जिसमें m∠L = 30°, m∠M = 70° और m∠N= 80° हैं।
हल :
(a) विषमबाहु त्रिभुज क्योंकि सभी भुजाओं की लम्बाइयाँ असमान हैं। .
(b) ∆ABC विषमबाहु त्रिभुज है, क्योंकि AB ≠ BC ≠ CA.
(c) ∵ PQ = QR = RP = 5 सेमी अर्थात् सभी भुजाओं की लम्बाइयाँ समान हैं।
∴ ∆PQR समबाहु त्रिभुज है।
(d) ∵ m∠D = 90°
∴ ∆DEF समकोण त्रिभुज है।
(e) ∵ m∠Y = 90° और XY = YZ
∴ ∆XYZ समद्विबाहु समकोण त्रिभुज है।
(f) ∵ m∠L = 30°, m∠M = 70° और m∠N = 80°
सभी कोण न्यून कोण हैं।
∴ ∆LMN न्यूनकोण त्रिभुज है।
प्रश्न 2.
निम्न का सुमेलन कीजिए :

उत्तर-
(i)→(e),
(ii)→ (g),
(iii)→ (a),
(iv)→ (f),
(v)→ (d)
(vi)→ (c),
(vii) → (b).
प्रश्न 3.
निम्नलिखित त्रिभुजों में से प्रत्येक का दो प्रकार से नामकरण कीजिए।
(आप कोण का प्रकार केवल देखकर ज्ञात कर सकते हैं।)

हल :
(a) न्यूनकोण त्रिभुज; समद्विबाहु त्रिभुज,
(b) समकोण त्रिभुज; विषमबाहु त्रिभुज,
(c) अधिक कोण त्रिभुज; समद्विबाहु त्रिभुज,
(d) समकोण त्रिभुज; समद्विबाहु त्रिभुज,
(e) न्यूनकोण त्रिभुज; समबाहु त्रिभुज,
(f) अधिक कोण त्रिभुज; विषमबाहु त्रिभुज।
प्रश्न 4.
माचिस की तीलियों की सहायता से त्रिभुज बनाने का प्रयत्न कीजिए। इनमें से कुछ आकृति पाठ्य-पुस्तक में दिखाई गई हैं। क्या आप निम्न से त्रिभुज बना सकते हैं ?
(a) 3 माचिस की तीलियाँ
(b) 4 माचिस की तीलियाँ
(c) 5 माचिस की तीलियाँ
(d) 6 माचिस की तीलियाँ
(ध्यान रखिए कि अपको प्रत्येक स्थिति में सभी उपलब्ध माचिस की तीलियों का उपयोग करना है।)
प्रत्येक स्थिति में त्रिभुज के प्रकार का नाम बताइए। यदि आप त्रिभुज नहीं बना पाते हैं, तो उसके कारण के बारे में सोचिए।
हल :
(a) हाँ, हम 3 माचिस की तीलियों से एक समबाहु त्रिभुज बना सकते हैं।
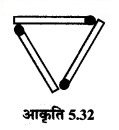
(b) नहीं, हम 4 माचिस की तीलियों से त्रिभुज नहीं बना सकते हैं क्योंकि त्रिभुज की दो भुजाओं की लम्बाइयों का योग तीसरी भुजा की लम्बाई से अधिक होना चाहिए।
(c) हाँ, 5 माचिस की तीलियों से हम समद्विबाहु त्रिभुज बना सकते हैं।

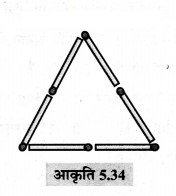
(d) हाँ, हम 6 माचिस की तीलियों से समबाहु त्रिभुज बना सकते हैं।
पाठ्य-पुस्तक पृष्ठ संख्या # 115
इन्हें कीजिए
प्रश्न 1.
(i) दो डण्डी लीजिए और इन्हें इस प्रकार रखिए कि उनका एक-एक सिरा एक सिरे पर मिले। अब डंडियों के एक अन्य युग्म को इस प्रकार रखिए कि उनके सिरे डंडियों के पहले युग्म के स्वतन्त्र सिरों से जुड़ जाएँ। इस प्रकार हमें क्या आकृति प्राप्त होती है ?

उत्तर-
(i) डंडियों को इस प्रकार रखने से हमें चतुर्भज आकृति प्राप्त होगी। इस चतुर्भुज की भुजाएँ
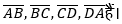
इस चतुर्भुज के चार कोण हैं। ये ∠BAD, ∠ADC, ∠DCB और ∠ABC हैं।
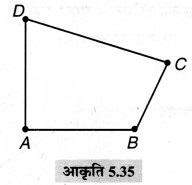
(ii) अन्य विकर्ण है।
भुजाओं और विकर्णों को मापने पर,
AB = 2.3 सेमी, BC = 1.5 सेमी, CD = 3.3 सेमी,
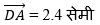
विकर्ण AC = 3.2 सेमी और BD = 3.4 सेमी
कोणों को मापने पर, ∠DAB = 93°, ∠ABC = 115°, ∠BCD = 82°, ∠CDA = 70°
प्रश्न 2.
जैसा आपने ऊपर क्रियाकलाप किया है, चार डंडियाँ लेकर इसे देखिए कि क्या आप इनसे ऐसा चतुर्भुज बना सकते हैं जिसमें
(a) चारों कोण न्यूनकोण हैं।
(b) एक कोण अधिक कोण है।
(c) एक कोण समकोण है।
(d) दो कोण अधिक कोण हैं।
(e) दो कोण समकोण हैं।
(f) विकर्ण परस्पर समकोण पर हैं।
उत्तर-
(a) नहीं,
(b) हाँ,
(c) हाँ,
(d) हाँ,
(e) हाँ,
(f) हाँ।
पाठ्य-पुस्तक पृष्ठ संख्या # 115-117
इन्हें कीजिए
प्रश्न 1.
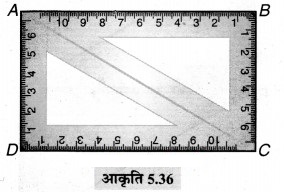
(a) सेट स्क्वे यर 30° – 60° – 90° के युग्म का प्रयोग
क्या आप इस प्रकार बने चतुर्भुज का नाम बता सकते हैं? इसके प्रत्येक कोण का माप क्या है ? आप अन्य कौन-से गुण ज्ञात कर सकते हैं?
उत्तर-
इस प्रकार बने चतुर्भज का नाम आयत है। इसके प्रत्येक कोण की माप 90° है।
(i) आयत की सम्मुख भुजाएँ समान होती हैं।
(ii) विकर्ण बराबर होते हैं तथा परस्पर समद्विभाजित करते हैं।
(b) सेट स्क्वे यर 45° – 45° – 90° के युग्म का प्रयोग
क्या आप देख सकते हैं कि सभी भुजाओं की लम्बाइयाँ बराबर हैं ? आप इसके कोणों और विकर्णों के बारे में क्या कह सकते हैं ? वर्ग के कुछ अन्य गुण ज्ञात करने का प्रयत्न कीजिए।
उत्तर-
हाँ, इस प्रकार बना चतुर्भुज वर्ग है। इसकी सभी भुजाओं की लम्बाइयाँ बराबर हैं?
वर्ग का प्रत्येक कोण 90° है।
(i) इसके विकर्ण बराबर हैं।
(ii) विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं।

(c) सेट स्क्वे यर 30° – 60° – 90° के युग्म का प्रयोग
(i) क्या आप देख रहे हैं कि इसकी सम्मुख भुजाएँ समान्तर हैं ?
(ii) क्या इसकी सम्मुख भुजाएँ बराबर हैं ?
(iii) क्या इसके विकर्ण बराबर हैं ?
उत्तर-
प्राप्त चित्र समान्तर चतुर्भुज है।
(i) हाँ, इसकी सम्मुख भुजाएँ समान्तर होती हैं।
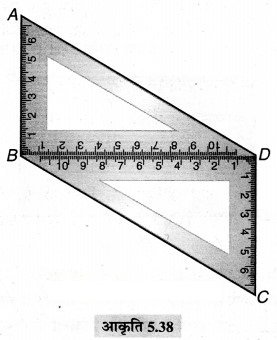
(ii) हाँ, इसकी सम्मुख भुजाएँ बराबर होती हैं।
(iii) नहीं, इसके विकर्ण बराबर नहीं होते हैं।
अन्य गुण-इसके सम्मुख कोण समान होते हैं।
आसन्न कोणों का योग 180° होता है।
इसके विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
(d) चार 30° – 60° – 90° सेट स्क्वे यर के प्रयोग से समचतुर्भुज प्राप्त होता है।
AB = BC = CD = DA;
AB || CD, AD || BC

(e) कई सेट स्क्वे यर का प्रयोग करने पर ऐसा चतुर्भुज प्राप्त होगा जिसकी दो भुजाएँ समान्तर होंगी।
यह (ABCD) एक समलम्ब है।
यहाँ BC || AD

पाठ्य-पुस्तक पृष्ठ संख्या # 117
यहाँ आपकी खोजों के सारांश की एक रूपरेखा दी जा रही है। इसे पूरा कीजिए।
