Chapter 5 रेखा एवं कोण Ex 5.1

Chapter 5 रेखा एवं कोण Ex 5.1

प्रश्न 1.
निम्नलिखित कोणों में से प्रत्येक का पूरक ज्ञात कीजिए :

हल:
चूँकि एक कोण और इसके पूरक कोण का योग एक समकोण अर्थात् 90° होता है। अतः

1. 20° का पूरक = 90 – 20° = 70°
2. 63° का पूरक = 90° – 63° = 27°
3. 57° का पूरक = 90° – 57° = 33°

प्रश्न 2.
निम्नलिखित कोणों में से प्रत्येक का सम्पूरक ज्ञात कीजिए:

हल:
चूँकि एक कोण और उसके सम्पूरक कोण का योग दो समकोण अर्थात् 180° होता है। अतः

1. 105° का सम्पूरक = 180° – 105° = 75°
2. 87° का सम्पूरक = 180° – 87° = 93°
3. 154° का सम्पूरक = 180° – 154° = 26°

प्रश्न 3.
कोणों के निम्नलिखित युग्मों में से पूरक एवं सम्पूरक युग्मों की पृथक-पृथक पहचान कीजिए :
(i) 65°, 115°
(ii) 63°, 27°
(iii) 112°,68°
(iv) 130°, 50°
(v) 45°, 45°
(vi) 80°, 10°
हल:
(i) ∵ 65° + 115° = 180°
∴ कोण 65° और 115° का युग्म सम्पूरक है।

(ii) ∵ 63° + 27° = 90°
∴ कोण 63° और 27° का युग्म पूरक है।

(iii) ∵ 112° + 68° = 180°
∴ कोण 112° और 68° का युग्म सम्पूरक है।

(iv) ∵ 130° + 50° = 180°
∴ कोण 130° और 50° का युग्म सम्पूरक है।

(v) ∵ 45° + 45° = 90°
∴ कोण 45° और 45° का युग्म पूरक है।

(vi) ∵ 80° + 10° = 90°
∴ कोण 80° और 10° का युग्म पूरक है।

प्रश्न 4.
ऐसा कोण ज्ञात कीजिए जो अपने पूरक के समान हो।
हल:
माना कि अभीष्ट कोण x° है।
प्रश्नानुसार, पूरक कोण = x°
∴ x° + x° = 90° (∵एक कोण और इसके पूरक कोण का योग 90° होता है)
या 2x = 90° या
x° = 90°/2 = 45°
अतः अभीष्ट समान कोण = 45°

प्रश्न 5.
ऐसा कोण ज्ञात कीजिए जो अपने सम्पूरक के समान हो।
हल:
माना कि अभीष्ट कोण x° है।
प्रश्नानुसार, सम्पूरक कोण = x°
∴ x° +x° = 180° (∵ एक कोण और इसके सम्पूरक कोण का योग 180° होता है)
या 2x° = 180°
या x° = 180°/2 = 90°
या अतः अभीष्ट समान कोण = 90°

प्रश्न 6.
दी हुई आकृति में ∠1 एवं ∠2 सम्पूरक कोण | हैं। यदि ∠1 में कमी की जाती है, तो ∠2 में क्या परिवर्तन होगा ताकि दोनों कोण फिर भी सम्पूरक ही रहें।

उत्तर:
दोनों कोणों का सम्पूरक बने रहने के लिए ∠1 जिस माप से घटेगा, ∠2 उसी माप से बढ़ेगा।

प्रश्न 7.
क्या दो ऐसे कोण सम्पूरक हो सकते हैं यदि उनमें से दोनों
(i) न्यून कोण हैं ?
(ii) अधिक कोण हैं ?
(iii) समकोण हैं ?
हल:
(i) नहीं, क्योंकि दो न्यून कोणों का योग 180° से कम होता है।
(ii) नहीं, क्योंकि दो अधिक कोणों का योग 180° से अधिक होता है।
(iii) हाँ, क्योंकि दो समकोणों का योग 180° होता है।

प्रश्न 8.
एक कोण 450 से बड़ा है। क्या इसका पूरक कोण 45° से बड़ा है अथवा 45° के बराबर है अथवा 450 से छोटा है?
उत्तर:
क्योंकि एक कोण और उसके पूरक कोण का योग 90° होता है। प्रश्नानुसार, दिया हुआ एक कोण 45° से बड़ा है। अतः इसका पूरक कोण 45° से छोटा होगा।

प्रश्न 9.
संलग्न आकृति में :
(i) क्या ∠ 1, ∠2 का आसन्न है ?
(ii) क्या ∠AOC, ∠AOE का आसन्न है ?
(iii) क्या ∠COE एवं ∠EOD रैखिक युग्म बनाते हैं ?
(iv) क्या ∠ BOD एवं ∠ DOA सम्पूरक हैं ?
(v) क्या ∠1 का ऊर्ध्वाधर सम्मुख कोण ∠4 है ?
(vi) ∠5 का ऊर्ध्वाधर सम्मुख कोण क्या है ?

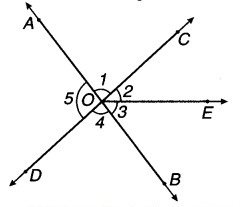
उत्तर:
(i) हाँ, ∠1 और ∠2 आसन्न कोण हैं।
(ii) ∠AOC, ∠AOE का आसन्न नहीं है, क्योंकि ∠AOC, ∠ AOE का एक हिस्सा है।
(iii) हाँ, ∠ COE और ∠EOD रैखिक युग्म बनाते हैं। क्योंकि एक सरल रेखा है।
(iv) हाँ, ∠BOD एवं ∠DOA सम्पूरक हैं, क्योंकि ∠ BOD+ ∠ DOA = 180°.
(v) हाँ, क्योंकि AB और CD सीधी रेखाएँ हैं।
(vi) 5 का ऊर्ध्वाधर सम्मुख कोण ∠ BOC (या ∠COB) अर्थात् (∠ 2 + ∠3) है।

प्रश्न 10.
पहचानिए कि कोणों के कौन से युग्म :
(i) ऊर्ध्वाधर सम्मुख कोण हैं।
(ii) रैखिक युग्म हैं।

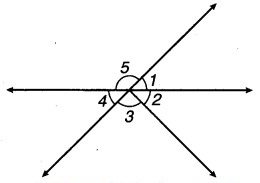
उत्तर:
(i) चित्र में, ∠1 और ∠4; ∠5 और (∠2 + ∠3) ऊर्ध्वाधर सम्मुख कोण हैं।
(ii) कोण ∠ 1, ∠5, ∠4, ∠5; ∠ 1, (∠2 + ∠3) व ∠4, (∠2 + ∠3) रैखिक युग्म बनाते हैं।

प्रश्न 11.
निम्नलिखित आकृति में क्या ∠1, ∠2 का आसन्न है ? कारण लिखिए।

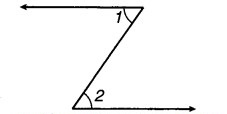
उत्तर:
∠1, ∠2 का आसन्न कोण नहीं है क्योंकि इनका कोई उभयनिष्ठ शीर्ष नहीं है।

प्रश्न 12.
निम्नलिखित में से प्रत्येक में कोण x, y एवं z के मान ज्ञात कीजिए।

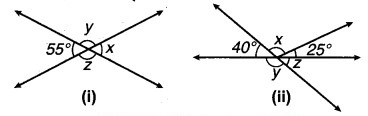
हल:
(i) ∵ x और 55° ऊर्ध्वाधर सम्मुख कोण हैं
∴ x = 55°
पुनः 55° + y = 180° (रैखिक युग्म)
या y = 180° – 55°
या y = 125°
चूँकि y और z ऊर्ध्वाधर सम्मुख कोण हैं
∴ z = 125°
अतः x = 55°, y = 125°, 2 = 125°

(ii) ∵z और 40° ऊर्ध्वाधर सम्मुख कोण हैं
∴ z = 40°
पुनः y और 40° रैखिक युग्म बनाते हैं
∴ y + 40° = 180°
या y = 180° – 40° = 140°
∴ और (x + 25°) ऊर्ध्वाधर सम्मुख कोण है
∴ x + 25° =y
अतः x + 25° = 140°
अतः x = 140° – 25° = 1150
अतः x = 115°, y= 140°, z = 40°

प्रश्न 13.
रिक्त स्थानों की पूर्ति कीजिए
(i) यदि दो कोण पूरक हैं, तो उनके मापों का योग …….. है।
(ii) यदि दो कोण सम्पूरक हैं, तो उनके मापों का योग …….. है।
(iii) रैखिक युग्म बनाने वाले दो कोण …….. होते हैं।
(iv) यदि दो आसन्न कोण सम्पूरक हैं, तो वे ……. बनाते हैं।
(v) यदि दो रेखाएँ एक-दूसरे को एक बिन्दु पर प्रतिच्छेद करती हैं, तो ऊर्ध्वाधर सम्मुख हमेशा …….. होते हैं।
(vi) यदि दो रेखाएँ एक-दूसरे को एक बिन्दु पर प्रतिच्छेद करती हैं और यदि ऊर्ध्वाधर सम्मुख कोणों का
एक युग्म न्यून कोण है, तो ऊर्ध्वाधर सम्मुख कोणों का | दूसरा युग्म …….. है।
हल:
(i) 90°,
(ii) 180°,
(iii) सम्पूरक,
(iv) रैखिक युग्म,
(v) समान,
(vi) अधिक कोण।

प्रश्न 14.
संलग्न आकृति में निम्नलिखित कोण युग्मों को नाम दीजिए:

(i) ऊर्ध्वाधर सम्मुख अधिक कोण
(ii) आसन्न पूरक कोण
(iii) समान सम्पूरक कोण
(iv) असमान सम्पूरक कोण
(v) आसन्न कोण जो रैखिक युग्म नहीं बनाते हैं।
उत्तर:
(i) ∠ BOC और ∠AOD ऊर्ध्वाधर सम्मुख अधिक कोण हैं।
(ii) ∠AOB और ∠AOE आसन्न पूरक कोण हैं।
(iii) ∠ BOE और ∠EOD समान सम्पूरक कोण हैं।
(iv) ∠AOE और ∠EOC असमान सम्पूरक कोण हैं।
(v) ∠ BOA और ∠AOE, ∠AOE और ∠EOD, ∠EOD और ∠COD.

पाठ्य-पुस्तक पृष्ठ संख्या # 116

सोचिए, चर्चा कीजिए एवं लिखिए

प्रश्न 1.
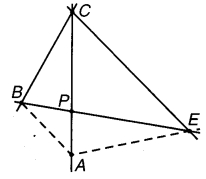
आकृति में AC और BE, P पर प्रतिच्छेद करती हैं। AC और BC, C पर प्रतिच्छेद करती हैं। AC और EC, C पर प्रतिच्छेद करती है। प्रतिच्छेदी रेखाखण्डों के दस अन्य युग्म ज्ञात करने का प्रयास कीजिए।

हल:
AB तथा AE को मिलाइए। प्रतिच्छेदी रेखाओं के अन्य युग्म
(i) B पर प्रतिच्छेद-
CB और EB, PB और CB

(ii) C पर प्रतिच्छेद
BC और EC, PC और BC, PC और EC
(iii) E पर प्रतिच्छेद
BE और CE, PE और CE
(iv) P पर प्रतिच्छेद
BP और CP, EP और CP
(v) A पर प्रतिच्छेद
PA और BA, PA और EA

प्रश्न 2.
क्या आप इस आकृति में दो रेखाखण्डों के युग्म ज्ञात कर सकते हैं, जो प्रतिच्छेदी नहीं हैं ?
हल:
हाँ, AB और EC तथा AE और BC न कटने वाले रेखाखण्डों के युग्म हैं।

प्रश्न 3.
क्या दो रेखाएँ एक से ज्यादा बिन्दुओं पर प्रतिच्छेद कर सकती हैं। इसके बारे में विचार कीजिए।
उत्तर:
नहीं, दो रेखाएँ एक से ज्यादा बिन्दुओं पर प्रतिच्छेद नहीं कर सकती हैं।

प्रयास कीजिए

प्रश्न 1.
अपने आस-पास के परिवेश में ऐसे उदाहरण ज्ञात कीजिए जहाँ रेखाएँ समकोण पर प्रतिच्छेद करती हैं।
उत्तर:
समकोण पर प्रतिच्छेद करने वाली रेखाएँ

1. श्यामपट के किनारे,
2. पुस्तक/उत्तर-पुस्तिका के किनारे,
3. आयताकार दरवाजे के किनारे,
4. मेज की टाँगें तथा उसके ऊपरी तख्ता आदि।

प्रश्न 2.
एक समबाहु त्रिभुज के शीर्षों पर प्रतिच्छेदी रेखाओं द्वारा निर्मित कोणों के माप ज्ञात कीजिए।
हल:
माना ABC एक समबाहु त्रिभुज है जिसमें प्रतिच्छेदी बिन्दु A, B और C हैं।
∵ AB = BC = CA

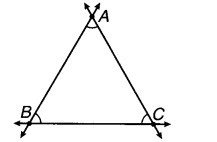
∵ ∠A = ∠B = ∠C = x (∵ समबाहु त्रिभुज के सभी कोण समान होते हैं)
∴∠B + ∠C = 180°
∴ x + x + x = 180°
∴ 3x = 180°
या
x = 180°/3 = 60°
अतः ∠A = ∠B = ∠C = 60°

प्रश्न 3.
एक आयत खींचिए और प्रतिच्छेदी रेखाओं द्वारा निर्मित चार शीर्षों के कोणों के माप ज्ञात कीजिए।
हल:
माना ABCD एक आयत है। अतः परिभाषा से, आयत का प्रत्येक कोण समकोण होता है।
∴ ∠A की माप = 90°, ∠B की माप = 90°.
∴ ∠C की माप = 90°, ∠D की माप = 90°

प्रश्न 4.
यदि दो रेखाएँ एक-दूसरे को प्रतिच्छेद करती हैं, तो क्या वे हमेशा एक-दूसरे को समकोण पर प्रतिच्छेद करती हैं ?
उत्तर:
नहीं, दो रेखाएँ हमेशा एक-दूसरे को समकोण पर प्रतिच्छेद नहीं करती हैं।

पाठ्य-पुस्तक पृष्ठ संख्या # 117

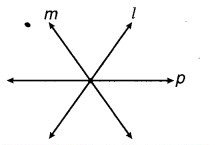
संलग्न आकृति में p एक तिर्यक छेदी रेखा नहीं है तथापि ये रेखाएँ l और m को काटती हैं। क्या आप बता सकते हैं, क्यों?

उत्तर:
रेखा p, रेखा l और m की तिर्यक रेखा नहीं है क्योंकि यह रेखाओं को अलग-अलग बिन्दुओं पर नहीं काटती है। वास्तव में दो रेखाओं को यह एक ही बिन्दु पर काटती है।

प्रयास कीजिए

प्रश्न 1.
मान लीजिए दो रेखाएँ दी हुई हैं। इन रेखाओं के लिए आप कितनी तिर्यक छेदी रेखाएँ खींच सकते हैं ?
उत्तर:
हम दो दी गई रेखाओं के लिए असंख्य तिर्यक छेदी रेखाएँ खींच सकते हैं।

प्रश्न 2.
यदि एक रेखा तीन रेखाओं की तिर्यक छेदी रेखा है, तो बताइए कितने प्रतिच्छेद बिन्दु हैं।
उत्तर:
अगर तीन रेखाओं की एक तिर्यक छेदी रेखा है, तो इसके केवल तीन भिन्न प्रतिच्छेद बिन्दु हैं।

प्रश्न 3.
अपने आस-पास कुछ तिर्यक छेदी रेखाएँ ढूँढ़ने का प्रयास कीजिए।
उत्तर:
तिर्यक छेदी रेखाओं के उदाहरण हैं-कपड़े सुखाने का स्टैण्ड, लोहे की सीढ़ी, खिड़की की ग्रिल आदि।

पाठ्य-पुस्तक पृष्ठ संख्या # 118

प्रयास कीजिए

प्रश्न 1.
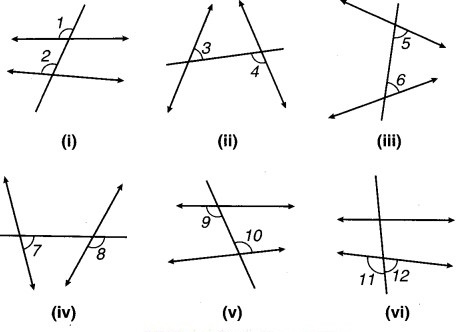
प्रत्येक आकृति में कोण-युग्म को नाम दीजिए-

उत्तर:
(i) ∠1 और ∠2 संगत कोण हैं।
(ii) ∠3 और ∠4 एकान्तर कोण हैं।
(iii) ∠5 और ∠6 तिर्यक छेदी रेखा के एक ही ओर के अन्तः कोण हैं।
(iv) ∠7 और ∠8 संगत कोण हैं।
(v) ∠9 और ∠10 एकान्तर कोण हैं।
(vi) ∠11 और ∠12 रैखिक युग्म हैं।

पाठ्य-पुस्तक पृष्ठ संख्या # 121

प्रयास कीजिए

(i) l || m
t एक तिर्यक छेदी रेखा है।
∠x = ?

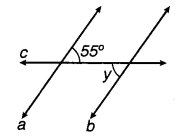
(ii) a || b
c एक तिर्यक छेदी रेखा है।
∠y = ?

(iii) l₁, l₂ दो रेखाएँ हैं।
t एक तिर्यक छेदी रेखा है।
क्या ∠1 = ∠2 हैं ?

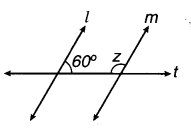
(iv) l || m
t एक तिर्यक छेदी रेखा है,
∠z = ?

(v) l || m
t एक तिर्यक छेदी रेखा है,
∠ x = ?

(iv) l || m, p || q
a, b, c, d ज्ञात कीजिए।
हल:
(i) x = 60° (∵ x और 60 एकान्तर कोण हैं)
(ii) y = 55°(∵ y और 55° एकान्तर कोण हैं)
(iii) नहीं, 2 1 और 2 2 बराबर नहीं हैं। (∵ 11 और 12 समान्तर नहीं हैं)
(iv) 60° + z = 180°
⇒ z = 180° – 60° = 120° (∵60° और 2 तिर्यक छेदी रेखा के एक ही ओर के कोण हैं)
(v) x = 120° (∵x और 120° संगत कोण हैं।)
(vi) a+ 60° = 180° (∵ a और 60° तिर्यक छेदी रेखा के एक ही ओर के कोण हैं)
∴ a = 180° – 60° = 120°
a + c = 180° (एकान्तर कोण)
c = 180 – a = 180° – 120° = 60°
c = b
⇒ b = 60° (ऊर्ध्वाधर सम्मुख कोण हैं)
b + d = 180° (रैखिका युग्म है)
⇒ 60 + d = 180°
⇒ d = 180° – 60° = 120°.

प्रयास कीजिए

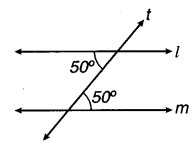
(i) क्या l || m है ? क्यों ?

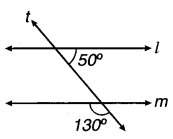
(ii) क्या l || m है ? क्यों ?

(iii) l ||m और तिर्यक छेदी रेखा है।
हल:
(i) यदि एक तिर्यक छेदी रेखा दो दी हुई रेखाओं को इस प्रकार काटे कि एकान्तर कोण समान हों, तो रेखाएँ समान्तर होती हैं।
∵ 50° = 50°
∴ एकान्तर कोण समान हैं।
अतः l || m.

(ii) माना चित्र (ii) में, ∠1 चिन्हित किया।
∠1 + ∠130° = 180° (रैखिक युग्म के कोण हैं)
∴ ∠1 = 180° – 130° = 50°
∵ संगत कोण समान हैं, अतः l || m

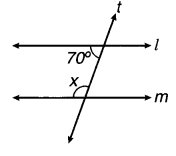
(iii) ∵ l || m और तिर्यक छेदी रेखा है।
∴ तिर्यक छेदी रेखा के एक ओर के अन्तः कोणों का योग
= 180°
x + 70° = 180°
या x = 180° – 70° = 110°