Chapter 5 Lines and Angles Exercise 5.1
Question 1.
Find the complement of each of the following angles:

Solution:
(i) Complement of 20° = 90° – 20° = 70°
(ii) Complement of 63° = 90° – 63° = 27°
(iii) Complement of 57° = 90° – 57° = 33°
Question 2.
Find the supplement of each of the following angles:
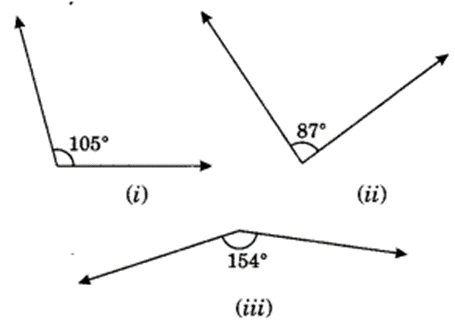
Solution:
(i) Supplement of 105° = 180° – 105° = 75°
(ii) Supplement of 87° = 180° – 87° = 93°
(iii) Supplement of 154° = 180° – 154° = 26°
Question 3.
Identify which of the following pairs of angles are complementary and which are supplementary?
(i) 65°, 115°
(ii) 63°, 27°
(iii) 112°, 68°
(iv) 130°, 50°
(v) 45°, 45°
(vi) 80°, 10°
Solution:
(i) 65° (+) 115° = 180°
They are supplementary angles.
(ii) 63° (+) 27° = 90°
They are complementary angles.
(iii) 112° (+) 68° = 180°
They are supplementary angles.
(iv) 130° (+) 50° = 180°
They are supplementary angles.
(v) 45° (+) 45° = 90°
They are complementary angles.
(vi) 80° (+) 10° = 90°
They are complementary angles.

Question 6.
In the given figure, ∠1 and ∠2 are supplementary angles.
If ∠1 is decreased, what changes should take place in∠2 so that both the angles still remain supplementary.

Solution:
∠1 + ∠2 = 180° (given)
If ∠1 is decreased by some degrees, then ∠2 will also be increased by the same degree so that the two angles still remain supplementary.
Question 7.
Can two angles be supplementary if both of them are:
(i) acute?
(ii) obtuse?
(iii) right?
(ii) Since, acute angle < 90°
∴ Acute angle + acute angle < 90° + 90° < 180° Thus, the two acute angles cannot be supplementary angles. (ii) Since, obtuse angle > 90°
∴ Obtuse angle + obtuse angle > 90° + 90° > 180°
Thus, the two obtuse angles cannot be supplementary angles.
(iii) Since, right angle = 90°
∴ right angle + right angle = 90° + 90° = 180°
Thus, two right angles are supplementary angles.
Question 8.
An angle is greater than 45°. Is its complementary angle greater than 45° or equal to 45° or less than 45 °?
Solution:
Given angle is greater than 45°
Let the given angle be x°.
∴ x > 45
Complement of x° = 90° – x° < 45° [ ∵ x > 45°]
Thus the required angle is less than 45°.
Question 9.
In the following figure:
(i) Is ∠1 adjacent to ∠2?
(ii) Is ∠AOC adjacent to∠AOE?
(iii) Do ∠COE and ∠EOD form a linear pair?
(iv) Are ∠BOD and ∠DOA supplementary?
(v) Is ∠1 vertically opposite angle to ∠4?
(vi) What is the vertically opposite angle of ∠5?

Solution:
(i) Yes, ∠1 and ∠2 are adjacent angles.
(ii) No, ∠AOC is not adjacent to ∠AOE. [ ∵ OC and OE do not lie on either side of common arm OA] .
(iii) Yes, ∠COE and ∠EOD form a linear pair of angles.
(iv) Yes, ∠BOD and ∠DOA are supplementary. [∵ ∠BOD + ∠DOA = 180°]
(v) Yes, ∠1 is vertically opposite to ∠4.
(vi) Vertically opposite angle of ∠5 is ∠2 + ∠3 i.e. ∠BOC.
Question 10.
Indicate which pairs of angles are:
(i) Vertically opposite angles
(ii) Linear pairs
Solution:
(i) Vertically opposite angles are ∠1 and ∠4, ∠5 and (∠2 + ∠3)

(ii) Linear pairs are
∠1 and ∠5, ∠5 and ∠4
Question 11.
In the following figure, is ∠1 adjacent to ∠2? Give reasons.
Solution:
No, ∠1 and∠2 are not adjacent angles.

Reasons:
(i) ∠1 + ∠2 ≠ 180°
(ii) They have no common vertex.
Question 12.
Find the values of the angles x, y and z in each of the following:

Solution:
From Fig. 1. we have
∠x = ∠55° (Vertically opposite angles)
∠x + ∠y = 180° (Adjacent angles)
55° + ∠y = 180° (Linear pair angles)
∴ ∠y = 180° – 55° = 125°
∠y = ∠z (Vertically opposite angles)
125° = ∠z
Hence, ∠x = 55°, ∠y = 125° and ∠z = 125°
(ii) 25° + x + 40° = 180° (Sum of adjacent angles on straight line)
65° + x = 180°
∴ x = 180° – 65° = 115°
40° + y = 180° (Linear pairs)
∴ y = 180° – 40° = 140°
y + z = 180° (Linear pairs)
140° + z = 180°
∴ z = 180° – 140° = 40°
Hence, x – 115°, y = 140° and z – 40°
Question 13.
Fill in the blanks:
(i) If two angles are complementary, then the sum of their measures is ______ .
(ii) If two angles are supplementary, then the sum of their measures is ______ .
(iii) Two angles forming a linear pair are ______ .
(iv) If two adjacent angles are supplementary, they form a ______ .
(v) If two lines intersect at a point, then the vertically opposite angles are always ______ .
(vi) If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are ______ .
Solution:
(i) 90°
(ii) 180°
(iii) Supplementary
(iv) Linear pair
(v) Equal
(vi) Obtuse angle
Question 14.
In the given figure, name the following pairs of angles.

(i) Obtuse vertically opposite angles.
(ii) Adjacent complementary angles.
(iii) Equal supplementary angles.
(iv) Unequal supplementary angles.
(v) Adjacent angles but do not form a linear pair.
Solution:
(i) ∠BOC and ∠AOD are obtuse vertically opposite angles.
(ii) ∠AOB and ∠AOE are adjacent complementary angles.
(iii) ∠EOB and ∠EOD are equal supplementary angles.
(iv) ∠EOA and ∠EOC are unequal supplementary angles.
(v) ∠AOB and ∠AOE, ∠AOE and ∠EOD, ∠EOD and ∠COD are adjacent angles but do not form a linear pair.









