Chapter 5 Triangles Ex 5.1
Question 1.
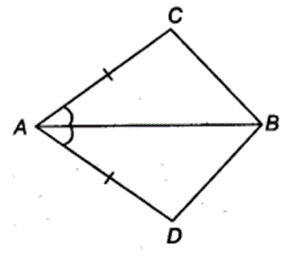
In quadrilateral ACBD, AC = AD and AB bisects ∠ A (see figure). Show that ∆ABC ≅ ∆ABD. What can you say about BC and BD?
Solution:
In ∆ABC and ∆ABD, we have
AC = AD (Given)
∠ CAB = ∠ DAB (∵ AB bisects ∠A)
and AB = AB (Common)
∴ ∆ ABC ≅ ∆ABD (By SAS congruence axiom)
∴ BC = BD (By CPCT)
Question 2.
ABCD is a quadrilateral in which AD = BC and ∠ DAB = ∠ CBA (see figure). Prove that
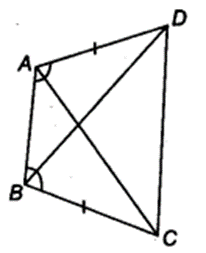
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠ BAC
Solution:
In ∆ ABC and ∆ BAC, we have
AD = BC (Given)
∠DAB = ∠CBA (Given)
and AB = AB (Common)
∴ ∆ ABD ≅ ∆BAC (By SAS congruence axiom)
Hence, BD = AC (By CPCT)
and ∠ABD= ∠BAC (By CPCT)
Question 3.
AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.
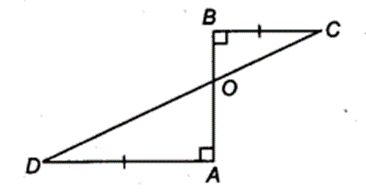
Solution:
In ∆AOD and ∆BOC, we have
∠AOD = ∠BOC
∵ AB and CD intersects at O.
∴ Which are vertically opposite angle
∵ ∠DAO = ∠CBO = 90°
and AD = BC (Given)
∴ ∆AOD ≅ ∆BOC (By SAS congruence axiom)
⇒ O is the mid-point of AB.
Hence, CD bisects AB.
Question 4.
l and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC = ∆CDA.
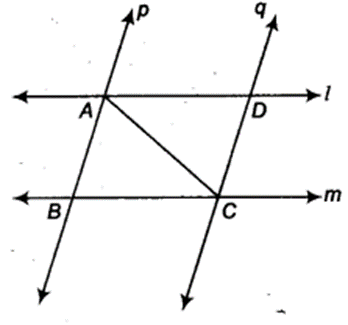
Solution:
From figure, we have
∠ 1 = ∠ 2 (Vertically opposite angles).. .(i)
∠ 1 = ∠ 6 (Corresponding angles)…(ii)
∠ 6 = ∠ 4 (Corresponding angles) …(iii)
From Eqs. (i) (ii) and (iii), we have
∠ 1 = ∠ 4
and ∠ 2 = ∠ 4 …..(iv)
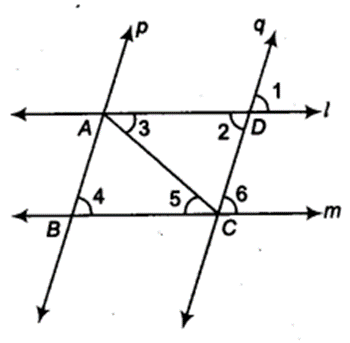
In ∆ABC and ∆CDA, we have
∠ 4 = ∠ 2 [From Eq. (iv]
∠5 = ∠ 3 (Alternate interior angles)
and AC = AC (Common)
∴ ∆ABC ≅ ∆ CDA (By AAS congruence axiom)
Question 5.
Line l is the bisector of an ∠ A and ∠ B is any point on l. BP and BQ are perpendiculars from B to the arms of LA (see figure). Show that
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms ot ∠A.
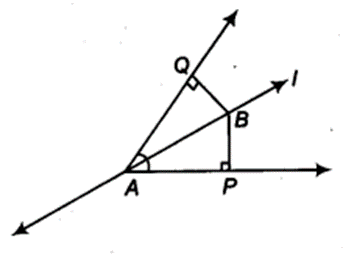
Solution:
In ∆ APB and ∆AQB, we have
∠ APB = ∠ AQB = 90°
∠ PAB = ∠ QAB (∵ AB bisects ∠ PAQ)
and AB = AB (Common)
∴ ∆ APB ≅ ∆ AQB (By AAS congruence axiom)
⇒ BP = BQ (By CPCT)
⇒ B is equidistant from the arms of ∠ A.
Question 6.
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
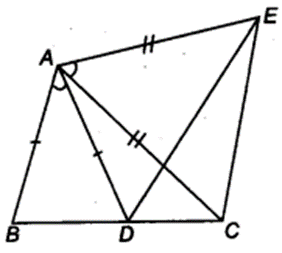
Solution:
In ∆ABC and ∆ADE, we have
AB = AD (Given)
∠ BAD = ∠ EAC (Given)…(i)
On adding ∠ DAC on both sides in Eq. (i)
⇒ ∠ BAD + ∠ DAC = ∠ EAC + ∠ DAC
⇒ ∠ BAC = ∠ DAE
and AC = AE (Given)
∴ ∆ABC ≅ ∆ADE (By AAS congruence axiom)
⇒ BC = DE (ByCPCT)
Question 7.
AS is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠ BAD = ∠ ABE and ∠ EPA = ∠ DPB. (see figure). Show that
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE
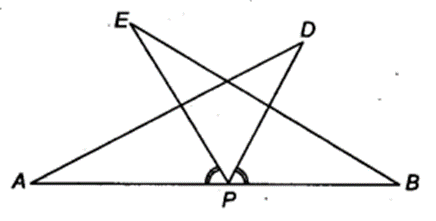
Solution:
We have,
AP = BP [∵ P is the mid-point of AB (Given)]… (i)
∠ EPA = ∠ DPB (Given)…(ii)
∠ BAD = ∠ ABE (Given).. .(iii)
On adding ∠ EPD on both sides in Eq. (ii); we have
⇒ ∠ EPA + ∠ EPD = ∠DPB + ∠ EPD
⇒ ∠ DP A = ∠ EPB …..(iv)
Now, In ∆DAP and ∆EBP, we have
∠ DPA = ∠ EPB [ From Eq(4)]
∠ DAP = ∠ EBP (Given)
and AP = BP [From Eq. (i)]
∴ ∆ DAP ≅ ∆ EBP (By ASA congruence axiom)
Hence, AD = BE (By CPCT)
Question 8.
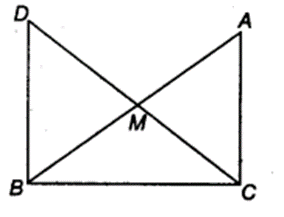
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB