Chapter 6 त्रिभुज Ex 6.5

Chapter 6 त्रिभुज Ex 6.5

प्रश्न 1.
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौनसे त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लम्बाई भी लिखिए।
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
हल-
(i) माना कि ∆ABC में,
AB = 7 cm, BC = 24 cm, AC = 25 cm
AB² + BC² = (7)² + (24)²
= 49 + 576
= 625
AC² = (25)² = 625
अब AB² + BC² = AC²
∴ ABC एक समकोण त्रिभुज है और कर्ण की लम्बाई = 25 cm है।

(ii) माना कि ∆PQR में,
PQ = 3 cm, QR = 8 cm, PR = 6 cm
PQ² + PR² = (3)² + (6)²
= 9 + 36
= 45
QR² = (8)² = 64
यहाँ PQ² + PR² ≠ QR²
∴ ∆PQR समकोण त्रिभुज नहीं है।

(iii) माना कि ∆MNP में,
MN = 50 cm, NP = 80 cm, MP = 100 cm
MN² + NP² = (50)² + (80)²
= 2500 + 6400
= 8900
MP² = (100)² = 10000
यहाँ MP² ≠ MN² + NP²
∴ ∆MNP समकोण त्रिभुज नहीं है।

(iv) माना कि ∆ABC में,
AB = 13 cm, BC = 12 cm, AC = 5 cm
BC² + AC² = (12)² + (5)²
= 144 + 25
= 169
AB² = (13)² = 169
∴ AB² = BC² + AC²
∆ACB समकोण त्रिभुज है।

प्रश्न 2.
PQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिन्दु M इस प्रकार स्थित है कि PM ⊥ QR है। दर्शाइए कि PM² = QM . MR है।
हल-
दिया है : समकोण ∆PQR में कोण P समकोण है।
QR पर बिन्दु M इस प्रकार स्थित है कि PM ⊥ QR है।
सिद्ध करना है : PM² = QM . MR

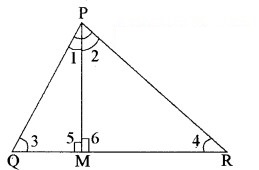
उपपत्ति : ∵ ∠P = 90° (दिया है)
∴ ∠1 + ∠2 = 90° ……(i)
∠M = 90°
∆PMO में,
∠1 + ∠3 + 90° = 180°
∠1 + ∠3 = 90° …….(ii)
[∠M = 90°]
(i) और (ii) से,
∠1 + ∠2 = ∠1 + ∠3
∠2 = ∠3
∆QPM और ∆RPM में,
∠3 = ∠2 (सिद्ध कर चुके हैं)
∠5 = ∠6 (प्रत्येक 90°)
∴ ∆QMP ~ ∆PMR [AA समरूपता]

[∵ यदि दो त्रिभुज समरूप हैं, तो उनके क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।]

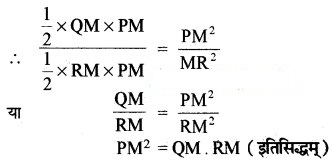
प्रश्न 3.
आकृति में, ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि

(i) AB = BC . BD
(ii) AC = BC . DC
(iiii) AD = BD . CD
हल-
∆DAB और ∆DCA में,
∠D = ∠D (उभयनिष्ठ कोण)
∠A = ∠C (प्रत्येक 90°)
∴ ∆DAB ~ ∆DCA …….(i) [AA समरूपता कसौटी से]
अब ∆DAB और ∆ACB में,
∠B = ∠B (उभयनिष्ठ कोण)
∠A = ∠C (प्रत्येक 90°)
∴ ∆DAB ~ ∆ACB
(i) और (ii) से,
∆DAB ~ ∆ACB ~ ∆DCA

प्रश्न 4.
ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है। सिद्ध कीजिए कि AB² = 2AC² है।
हल-
दिया है : ∆ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है।
सिद्ध करना है : AB² = 2AC²

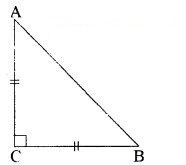
उपपत्ति : ∆ACB में, ∠C = 90°
AC = BC (दिया है)
AB² = AC² + BC² [पाइथागोरस प्रमेय से]
AB² = AC² + AC² [∵ BC = AC]
AB² = 2AC² (इतिसिद्धम्)

प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है। यदि AB² = 2AC² है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है।
हल-
दिया है : ∆ABC एक समद्विबाहु त्रिभुज है जिसकी भुजा AC = BC है।
तथा AB² = 2AC²
सिद्ध करना है : ∆ABC एक समकोण त्रिभुज है।

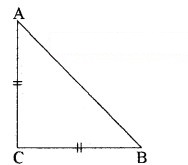
उपपत्ति : AB² = 2AC² (दिया है)
AB² = AC² + AC²
AB² = AC² + BC² [∵ AC = BC]
∴ पाइथागोरस प्रमेय के विलोम से, ∆ABC समकोण त्रिभुज है। (इतिसिद्धम्)

प्रश्न 6.
एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्ष लम्ब की लम्बाई ज्ञात कीजिए।
हल-
∆ABC समबाहु त्रिभुज है जिसकी भुजा 2a है।
AD ⊥ BC
AB = AC = BC = 2a
∆ADB ≅ ∆ADC [RHS सर्वांगसमता से]
∴ BD = DC = a

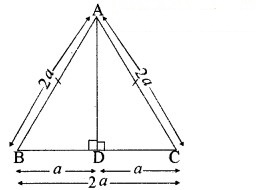
अब समकोण ∆ADB में,
AB² = AD² + BD²
⇒ (2a)² = AD² + (a)²
⇒ 4a² – a² = AD²
⇒ AD² = 3a²
⇒ AD = √3a

प्रश्न 7.
सिद्ध कीजिए कि एक समचतर्भज की भजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है।
हल-
दिया है : समचतुर्भुज ABCD के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं।
सिद्ध करना है : AB² + BC² + CD² + AD² = AC² + BD²
उपपत्ति : समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित होते हैं।

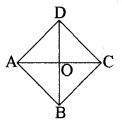
∴ AO = CO, BO = DO
∴ O पर कोण समकोण है
∆AOB में, ∠AOB = 90°
∴ AB² = AO² + BO² …….(i)
इसी प्रकार, BC² = CO² + BO² ……..(ii)
CD² = CO² + DO² …….(iii)
और DA² = DO² + AO² …….(iv)
(i), (ii), (iii) और (iv) को जोड़ने पर
AB² + BC² + CD² + DA² = 2AO² + 2CO² + 2BO² + 2DO²
= 4AO² + 4BO² [∵ AO = CO और BO = DO]
= (2AO)² + (2BO)²
= AC² + BD²
∴ AB² + BC² + CD² + AD² = AC² + BD² (इतिसिद्धम्)

प्रश्न 8.
आकृति में, ∆ABC के अभ्यन्तर में स्थित कोई बिन्दु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि-
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD²+ CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF²

हल-
दिया है : एक ∆ABC जिसमें OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है।
सिद्ध करना है :
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF²

रचना : OA, OB और OC को मिलाइए।
उपपत्ति : (i) समकोण ∆AFO में,
OA² = OF² + AF² [पाइथागोरस प्रमेय से]
या AF² = OA² – OF² …….(i)
समकोण ∆BDO में,
OB² = BD² + OD² [पाइथागोरस प्रमेय से]
⇒ BD² = OB² – OD² ……(ii)
समकोण ∆CEO में,
OC² = CE² + OE² [पाइथागोरस प्रमेय से]
⇒ CE² = OC² – OE² …….(iii)
(i), (ii), (iii) को जोड़ने पर
∴ AF² + BD² + CE² = OA² – OF² + OB² – OD² + OC² – OE²
= OA² + OB² + OC² – OD² – OE² – OF² (इतिसिद्धम्)
(ii) पुनः AF² + BD² + CE²
= (OA² – OE²) + (OC² – OD²) + (OB² – OF²)
= AE² + CD² + BF²
[∵ AE² = AO² – OE², CD² = OC² – OD², BF² = OB² – OF²]
(इतिसिद्धम्)

प्रश्न 9.
10 m लम्बी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8 m की ऊँचाई पर स्थित एक खिड़की तक पहुँचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।
हल-
प्रश्नानुसार, खिड़की की धरती से ऊँचाई (PQ) = 8 m

सीढ़ी की लम्बाई (PR) = 10 m
सीढ़ी के निचले सिरे और दीवार के आधार के बीच की दूरी QR = ?
समकोण ∆PQR में,
PQ² + QR² = PR² [पाइथागोरस प्रमेय से]
⇒ (8)² + (QR)² = (10)²
⇒ 64 + QR² = 100
⇒ QR² = 100 – 64
⇒ QR² = 36
⇒ QR = 6 m
∴ सीढ़ी के निचले सिरे और दीवार के आधार के बीच की दूरी = 6 m

प्रश्न 10.
18 m ऊँचे एक ऊर्ध्वाधर खम्भे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूटे से जुड़ा हुआ है। खम्भे के आधार से बँटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लम्बाई 24 m है।
हल-
माना कि खम्भे की ऊँचाई AB = 18 m
तार की लम्बाई AC = 24 m

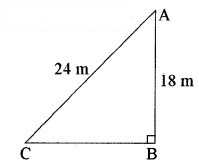
C खूटे की स्थिति है। इसकी खम्भे के आधार से दूरी BC = है।
समकोण ∆ABC में,
AB² + BC² = AC²
⇒ (18)² + (BC)² = (24)²
⇒ 324 + (BC)² = 576
⇒ BC² = 576 – 324
⇒ BC = √252
⇒ BC = 6√7 m
अतः खम्भे के आधार से खूटे की दूरी = 6√7 m = 15.87 m

प्रश्न 11.
एक हवाई जहाज एक हवाई अड्डे से उत्तर की ओर 1000 km/hr की चाल से उड़ता है। इसी समय एक अन्य हवाई जहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 km/hr की चाल से उड़ता है। 11/2 घण्टे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी?
हल-
पहले हवाई जहाज की चाल = 1000 km/hr

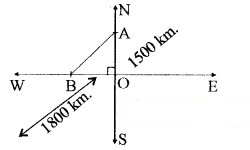
प्रश्न 12.
दो खम्भे जिनकी ऊँचाइयाँ 6 m और 11 m हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके ऊपरी सिरों के बीच की दूरी 12 m है तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
हल-
प्रश्नानुसार, पहले खम्भे की ऊँचाई, AB = 11 m
दूसरे खम्भे की ऊँचाई (CD) = 6 m

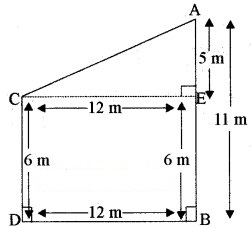
खम्भों के बीच की दूरी = 12 m
C से CE ⊥ AB खींचिए
BE = DC = 6 m
AE = AB – BE
= (11 – 6) m
= 5 m
समकोण ∆AEC में,
AC² = AE² + EC²

= √169
= 13
∴ खम्भों के ऊपरी सिरों के बीच की दूरी = 13 m

प्रश्न 13.
एक त्रिभुज ABC जिसका कोण C समकोण है, की भुजाओं CA और CB पर क्रमशः बिन्दु D और E स्थित हैं। सिद्ध कीजिए कि AE² + BD² = AB² + DE² है।
हल-
दिया है : ∆ABC एक समकोण त्रिभुज है जिसमें C पर समकोण है, भुजाओं CA और CB पर क्रमशः बिन्दु D और E स्थित हैं।
अर्थात् CD = AD = 1/2 AC
BE = EC = 1/2BC
सिद्ध करना है : AE² + BD² = AB² + DE²
उपपत्ति : समकोण ∆BCA में,
AB² = BC² + CA² (पाइथागोरस प्रमेय से) …….(i)

समकोण ∆ECD में,
DE² = EC² + DC² ……(ii) [पाइथागोरस प्रमेय से]
समकोण ∆ACE में,
AE² = AC² + CE² ……..(iii)
समकोण ∆BCD में,
BD² = BC² + CD² ……(iv)
(iii) और (iv) को जोड़ने पर,
AE² + BD² = AC² + CE² + BC² + CD²
= [AC² + CB²] + [CE² + DC²]
= AB² + DE²
अत: AE² + BD² = AB² + DE² (इतिसिद्धम्)

प्रश्न 14.
किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिन्दु पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है (देखिए आकृति)। सिद्ध कीजिए कि 2AB² = 2AC² + BC² है।

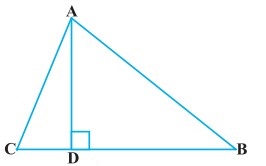
हल-
दिया है : ∆ABC में AD ⊥ BC तथा BD = 3CD है।
सिद्ध करना है : 2AB² = 2AC² + BC²
उपपत्ति : समकोण त्रिभुजों ADB और ADC में,
AB² = AD² + BD²
AC² = AD² + DC²;

प्रश्न 15.
किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि BD = 1/3BC है। सिद्ध कीजिए कि 9AD² = 7AB² है।
हल-
दिया है : एक समबाहु त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि BD = 1/3BC
सिद्ध करना है : 9AD² = 7AB²

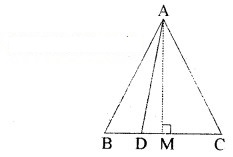
रचना : A से BC पर AM लम्ब खींचा अर्थात् AM ⊥ BC है।
उपपत्ति: ∆AMB ≅ ∆AMC 
[RH.S. नियम से क्योंकि AM = AM और AB = AC]
∴ BM = MC = 1/2
पुनः BD = 1/3BC

या 9AD² = 7AB² (इतिसिद्धम्)

प्रश्न 16.
किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्ष लम्ब के वर्ग के चार गुने के बराबर होता है।
हल-
दिया है : ∆ABC एक समबाहु ∆ है जिसमें AB = BC = AC तथा AD ⊥ BC

सिद्ध करना है : 3AB² = 4AD²
उपपत्ति : ∆ABC में, समबाहु त्रिभुज के लिये
AB = BC = AC = 2a (माना)
∵ AD ⊥ BC
∴ BD = DC = 1/2 BC = a
समकोण त्रिभुज ADB में,
AB² = AD² + BD²
⇒ (2a)² = AD² + (a)²
⇒ 4a² = AD² + a²
⇒ 4a² – a² = AD²
⇒ AD² = 3a²

⇒ 3AB² = 4AD² (इतिसिद्धम्)

प्रश्न 17.
सही उत्तर चुनकर उसका औचित्य दीजिए :
∆ABC = AB = 6√3 cm, AC = 12 cm और BC = 6 cm है। कोण B है :
(A) 120°
(B) 60°
(C) 90°
(D) 45°
हल-
AC = 12 cm, AB = 6√3 cm, तथा BC = 6 cm
AC² = (12)² = 144 cm
AB² + BC² = (6√3)² + (6)²
⇒ AB² + BC² = 108 + 36
⇒ AB² + BC² = 144 = (12)² = AC²
∴ AB² + BC² = AC²
पाइथागोरस प्रमेय के विलोम से,
∆ABC में B पर समकोण है
∴ ∠B = 90°
∴ सही विकल्प (C) 90°