Chapter 6 सम्मिश्र संख्याएँ और द्विघातीय समीकरण Ex 6.1
प्रश्न 1.
हल कीजिए 24x < 100, जब
(i) x एक प्राकृत संख्या है।
(ii) x एक पूर्णांक है।
हल:
24x < 100
24 से दोनों पक्षों में भाग करने पर
x < 30/−12 अर्थात x < −5/2 (i) यदि x एक प्राकृत संख्या है तो हल {1, 2, 3, 4} है। (ii) यदि x एक पूर्णांक संख्या है तो हल {……. – 3, -2, -1, 0, 1, 2, 3, 4}. प्रश्न 2. हल कीजिए : 12x > 30, जब
(i) x एक प्राकृत संख्या है।
(ii)x एक पूर्णांक है।
हल:
– 12x > 30
– 12 से दोनों पक्षों में भाग करने पर,
![]()
(i) यदि x प्राकृत संख्या है तो कोई हल नहीं है।
(ii) यदि x पूर्णाक संख्या है तो हल {…..-5, -4 ,-3} है।
प्रश्न 3.
हल कीजिए : 5x – 3 < 7, जब
(i) x एक पूर्णांक है।
(ii) x एक वास्तविक संख्या है।
हल:
5x – 3 < 7
दोनों पक्षों में 3 जोड़ने पर,
5x < 10
5 से भाग देने पर .
x < 10/5 अर्थात x < 2 (i) यदि x एक पूर्णांक संख्या है तो हल {….-2, –1, 0, 1}. (ii) यदि x एक वास्तविक संख्या है तो हल x ϵ (- ∞, 2). प्रश्न 4. हल कीजिए : 3x + 8 > 2, जब
(i) x एक पूर्णांक है।
(ii) x एक वास्तविक संख्या है।
हल:
3x + 8 > 2
3x > 2 – 8 या 3x > – 6
3 से भाग करने पर
x > – 6/3 या x> – 2
(i) यदि x एक पूर्णांक संख्या है तो हल {-1, 0, 1, 2 ,….}.
(ii) यदि x एक वास्तविक संख्या है तो हल x ϵ (-2, ∞).
प्रश्न 5.
हल कीजिए : 4x + 3 < 6x + 7.
हल :
4x + 3 < 6x + 7
6x को बाएँ पक्ष में तथा 3 को दाएँ पक्ष में रखने पर,
4x – 6x < 7 – 3
![]()
दी हुई असमिका का हल है : x ϵ (- 2, ∞).
प्रश्न 6.
हल कीजिए :
3x – 7 > 5x – 1.
हल:
3x – 7 > 5x – 1
5x का बाएँ पक्ष में और 7 को दाएँ पक्ष मे रखने पर,
3x – 5x > – 1 + 7
– 2x > 6
– 2 से भाग देने पर
x < – 3
∴ दी हुई असमिका का हल है x ϵ (- ∞, – 3).
प्रश्न 7.
हल कीजिए : 3(x – 1) ≤ 2 (x – 3).
हल:
असमिका
3(x – 1) ≤ 2 (x – 3)
3x – 3 ≤ 2x – 6
2x को बाएँ पक्ष में और 3 को दाएँ पक्ष में रखने पर,
3x – 2x ≤ 3 – 6
या x ≤ – 3
∴ हल है : x ϵ (- ∞, – 3].
प्रश्न 8.
हल कीजिए:
3(2 –x) ≥ 2 (1 –x).
हल:
दी हुई असमिका
3(2 – x) ≥ 2 (1 – x)
6 – 3x ≥ 2 – 2x
2x को बायीं ओर तथा 6 को दायीं ओर रखने पर,
2x – 3x ≥ 2 – 6.
या – x ≥ – 4 या x ≤ 4
∴ हल है : x ϵ (- ∞, 4].
प्रश्न 9.
![]()
हल:
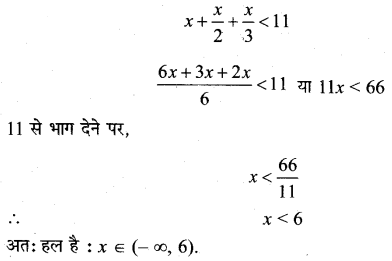


प्रश्न 11.

दोनों ओर 15 से गुणा करने पर
9(x – 2) ≤ 5 (2 –x)
या 9x – 18 ≤ 50 – 25x
25x को बायीं ओर तथा 18 को दायीं ओर रखने पर,
9x + 25x ≤ 50 + 18
या 34x ≤ 68
या x ≤ 2
∴ दी हुई असमिका का हल है x ϵ (- ∞, 2].
प्रश्न 12 .
![]()
हल:
दी हुई असमिका

प्रश्न 13.
हल कीजिए :
2(2x + 3) – 10 < 6 (x – 2).
हल:
दी हुई असमिका
2(2x + 3) – 10 < 6(x – 2)
4x + 6 – 10 < 6x – 12
6x को बायीं ओर तथा — 4 को दायीं ओर रखने पर,
4x – 6x < – 12 +4
या – 2x < – 8 (- 1) से गुणा करने पर, x > 4
∴ हल है : x ϵ (4, ∞)
प्रश्न 14.
हल कीजिए: 37 – (3x + 5) ≥ 9x – 8(x – 3).
हल:
दी हुई असमिका
37 – (3x + 5) ≥ 9x – 8(x – 3)
37 – 3x-5 ≥ 9x – 8x + 24
– 3x + 32 ≥ x + 24
x को बायीं ओर तथा 32 को दायीं ओर रखने पर
– 3x – x ≥ 24 – 32
या – 4x ≥ – 8
(- 1) से गुणा करने पर तथा 4 से भाग देने पर
x ≤ 84 या x ≤ 2
∴ हल है : x ϵ (- ∞, 2].
प्रश्न 15.

60 से दोनों पक्षों में गुणा करने पर ।
15x < 20(5x – 2) – 12 (7x – 3)
या 15x < 100x – 40 – 84x + 36
या 15x < 16x – 4
16x को बायीं ओर लाने पर,
15x – 16x < – 4
या – X < – 4 – 1 से गुणा करने पर x > 4
∴ हल है :
x ϵ (4, ∞)
प्रश्न 16.

60 से गुणा करने पर,
20(2x – 1 ) ≥ 15(3x – 2) – 12(2 –x)
या 40x – 20 ≥ 45x – 30 – 24 + 12x
या 40x – 20 ≥ 57x – 54
57x को बायीं ओर तथा 20 को दायीं ओर रखने पर,
40x – 57x ≥ – 54 + 20
– 17x ≥ – 34
– 17 से भाग देने पर
x ≤ 2
∴ हल है :
x ϵ (- ∞, 2].
प्रश्न 17.
से 20 तक की असमिकाओं का हल ज्ञात कीजिए तथा उन्हें संख्या रेखा पर आलेखित कीजिए।
प्रश्न 17.
3x – 2 < 2x + 1.
हल:
दी हुई असमिका 3x – 2 < 2x + 1
2x को बायीं ओर तथा 2 को दायीं ओर रखने पर,
3x – 2x < 1 + 2
या x <3
∴ हल है :
x ϵ (- ∞, 3].
![]()
प्रश्न 18.
5x – 3 ≥ 3x -5.
हल:
दी हुई असमिका 5x – 3 ≥ 3x – 5
3x को बायीं ओर तथा 3 को दायीं ओर रखने पर,
5x – 3x ≥ – 5 +3
या 2x ≥ – 2
2 से भाग देने पर
x ≥ – 1
∴ हल है x = [- 1, ∞).
![]()
प्रश्न 19.
3(1 – x) < 2 (x + 4)
हल:
दी हुई असमिका
3(1 – x) < 2 (x + 4)
3 – 3x < 2x +8
2x को बायीं ओर तथा 3 को दायीं ओर रखने पर,
– 3x – 2x < 8 – 3
या – 5x < 5 – 5 से भाग देने पर x > – 1
∴ हल है :
x ϵ (- 1, ∞)
![]()
प्रश्न 20.

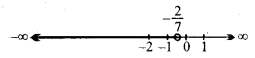
प्रश्न 21.
रवि ने पहली दो एकक परीक्षा में 70 और 75 अंक प्राप्त किए हैं। वह न्यूनतम अंक ज्ञात कीजिए, जिसे वह तीसरी एकक परीक्षा में पाकर 60 अंक का न्यूनतम औसत प्राप्त कर सके।
हल:
मान लीजिए तीसरे एकक परीक्षा में x अंक प्राप्त किए।
![]()

3 से दोनों पक्षों में गुणा करने पर,
145 + x ≥ 180
या x ≥ 180 – 145
या x ≥ 35
अतः रवि को तीसरी परीक्षा में 35 से अधिक या उसके बराबर अंक प्राप्त करने हैं।
प्रश्न 22.
किसी पाठ्यक्रम में ग्रेड A पाने के लिए एक व्यक्ति को सभी पाँच परीक्षाओं (प्रत्येक 100 अंकों में से) में 90 अंक या अधिक अंक का औसत प्राप्त करना चाहिए यदि सुनीता के प्रथम चार परीक्षाओं के प्राप्तांक 87,92, 94 और 95 हों तो वह न्यूनतम अंक ज्ञात कीजिए जिसे पांचवीं परीक्षा में प्राप्त करके सुनीता उस पाठ्यक्रम में ग्रेड A पाएगी।
हल:

5 से दोनों पक्षों में गुणा करने पर
368 + x ≥ 5 x 90
या 368 + x ≥ 450
या x ≥ 450 – 368
∴ x ≥ 82
अतः सुनीता को पाँचवीं परीक्षा में 82 से अधिक या उसके बराबर अंक प्राप्त करने चाहिए।
प्रश्न 23.
10 से कम क्रमागत विषम संख्याओं के ऐसे युग्म ज्ञात कीजिए जिनके योगफल 11 से अधिक हों।
हल:
मान लीजिए x और x + 2 दो विषम परिमेय संख्याएँ हैं।
x तथा x + 2 दोनों ही 10 से कम हैं।
⇒ x < 10 और x + 2 < 10 या x < 8 दोनों का योग 11 से अधिक है। ∴ x + (x + 2) > 11
या 2x + 2 > 11 या 2x > 11 – 2
∴ 2x > 9 या x > 9/2, या x > 4 1/2
अर्थात् यदि x = 5 हो, तब दूसरी संख्या = x + 2 = 7
इसी प्रकार यदि x = 7, तो x + 2 = 9
∴ दूसरा युग्म (7, 9)
x = 9 नहीं हो सकता क्योंकि x + 2 = 11 > 10
अत: वांछित युग्म है (5, 7), (7, 9).
प्रश्न 24.
क्रमागत सम संख्याओं के ऐसे युग्म ज्ञात कीजिए जिनमें से प्रत्येक 5 से बड़े हों, तथा उनका योगफल 23 से कम हो।
हल:
मान लीजिए x और x + 2 दो सम संख्याएँ हैं।
x और x + 2 दोनों ही 5 से बड़ी है।
⇒ x > 5
और x + (x + 2) < 23
∴ 2x + 2 < 23
या 2x < 23 – 2 = 21
∴ 2x < 21 या x < 21/2
यदि x = 10, x + 2 = 12 ⇒ x + (x + 2) < 23
इसी प्रकार (6, 8), (8, 10) युग्म भी दी हुई शर्त पूरी करते हैं।
वांछित युग्म (6, 8), (8, 10), (10, 12).
प्रश्न 25.
एक त्रिभुज की सबसे बड़ी भुजा सबसे छोटी भुजा की तीन गुनी है तथा त्रिभुज की तीसरी भुजा सबसे बड़ी भुजा से 2 सेमी कम है। तीसरी भुजा की न्यूनतम लंबाई ज्ञात कीजिए जबकि त्रिभुज का परिमाप न्यूनतम 61 सेमी है।
हल:
मान लीजिए त्रिभुज की सबसे छोटी भुजा = x सेमी
सबसे बड़ी भुजा = 3x सेमी
तीसरी भुजा = 3x – 2 सेमी
प्रश्नानुसार
x + 3x + (3x – 2) ≥ 61
7x – 2 ≥ 61
7x ≥ 61 + 2 = 63
⇒ x ≥ 9
∴ सबसे छोटी भुजा 9 सेमी है।
प्रश्न 26.
एक व्यक्ति 91 सेमी लंबे बोर्ड में से तीन लंबाईयाँ काटना चाहता है। दूसरी लंबाई सबसे छोटो लंबाई से 3 सेमी अधिक और तीसरी लंबाई सबसे छोटी लंबाई की दूनी है। सबसे छोटे बोर्ड की संभावित लंबाई क्या है, यदि तीसरा टुकड़ा दूसरे टुकड़े से कम से कम 5 सेमी अधिक लंबा हो ?
हल:
मान लीजिए कटे हुए सबसे छोटे बोर्ड की लंबाई = x सेमी.
दूसरे कटे हुए बोर्ड की लम्बाई = x + 3
तीसरे कटे हुए बोर्ड की लम्बाई = 2x सेमी
दिया है कि
x + (x + 3) + 2x ≤ 91
या 4x + 3 ≤ 91
या 4x + 3 ≤ 91 – 3
या 4x ≤ 88
x ≤ 22 …(1)
∴ यह भी दिया गया है कि 2x ≥ (x + 3) +5
2x ≥ x +8
x ≥ 8
∴ सबसे छोटे बोर्ड की लम्बाई कम से कम 8 सेमी हो और अधिक से अधिक 22 सेमी हो। …(2)