Chapter 6 सम्मिश्र संख्याएँ और द्विघातीय समीकरण Ex 6.3
प्रश्न 1 से 15 तक निम्नलिखित असमिकाओं को आलेखीय विधि से हल कीजिए :
प्रश्न 1.
x ≥ 3, y ≥ 2
हल:
x ≥ 3, y ≥ 2
(i) सरल रेखा x = 3 बिन्दु (3, 0) और (3, 2) से होकर जाती है।
x ≥ 3 में x = 0 रखने पर 0 ≥ 3, यह सत्य नहीं है।
∴ मूल बिन्दु (0, 0) x ≥ 3 के क्षेत्र में नहीं है।
(ii) सरल रेखा y = 2 बिन्दु (0, 2) और (3, 2) से होकर जाती है।
y ≥ 2 में y = 0 रखने पर
0 ≥ 2, यह सत्य नहीं है।
∴ मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है।
x ≥ 3 और y ≥ 2 का हल उभयनिष्ठ छायांकित क्षेत्र से दर्शाया गया है।

प्रश्न 2.
3x + 2y ≤ 12, x ≥ 1, y ≥ 2.
हल:
दी हुई रैखिक असमिकाएँ 3x + 2y ≤ 12, x ≥ 1, y ≥ 2
(i) रेखा 3x + 2y = 12 बिन्दु (2, 0) और (0, 6) से होकर जाती है।
3x + 2y ≤ 12 में x = 0, y = 0 रखने पर
0 + 0 ≤ 12, अर्थात् 0 ≤ 12 जो सत्य है।
∴ मूल बिन्दु (0, 0) इसके क्षेत्र में है।
3x + 2y ≤ 12 के हल में वे सभी बिन्दु हैं जो AB के नीचे है।

(ii) रेखा x = 1 बिन्दु B(1, 0), Q(1, 2) से होकर जाती है
x ≥ 1 में x = 0 रखने पर
0 ≥ 1, यह सत्य नहीं है।
∴ मूल बिन्दु इसके क्षेत्र में नहीं है।
∴ x ≥ 1 का हल के सभी बिन्दु है जो है जो x = 1 के दाईं ओर है।
(iii) रेखा y = 2, बिन्दु C(0, 2) और D(3, 2) से होकर जाती है।
y ≥ 2 में y = 0 रखने पर 0 ≥ 2, यह सत्य नहीं है।
∴ मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है।
y ≥ 2 का हल वे सब बिन्दु हैं जो y = 2 के ऊपर हैं।
तीनों असमिकाओं का हल इसके उभयनिष्ठ क्षेत्र ∆PQR के सभी बिन्दु हैं।
प्रश्न 3.
2x + y ≥ 6, 3x + 4y ≤ 12.
हल:
दी हुई असमिकाएँ 2x + y ≥ 6, 3x + 4y ≤ 12
(i) सरल रेखा 2x + y = 6 बिन्दु (3, 0) तथा (0, 6) से होकर जाती है।
2x + y ≥ 6 में x = 0, y = 0 रखने पर 0 ≤ 6 जो सत्य नहीं है।
∴ मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है। 2x +y ≥ 6 का हल वे सभी बिन्दु हैं जो 2x + y = 6 के ऊपर है।

(ii) सरल रेखा 3x + 4y = 12 बिन्दु D(4,0) और C(0, 3) से होकर जाती है।
3x + 4y ≤ 12 में x = 0, y = 0 रखने पर 0 + 0 ≤ 12, जो सत्य है।
∴ मूल बिन्दु (0, 0) इसके क्षेत्र में है।
अत: 3x + 4y ≤ 12 का हल वे सब बिन्दु हैं जो रेखा CD के नीचे हैं।
इस प्रकार 2x + y ≥ 6, 3x + 4y ≤ 12 का हल वह उभयनिष्ठ क्षेत्र है जो 2x + y = 6 के ऊपर और 3x + 4y = 12 के नीचे है। यह चित्र में उभयनिष्ठ क्षेत्र द्वारा दर्शाया गया है।
प्रश्न 4.
x + y > 4, 2x – y > 0.
हल:
दी हुई रैखिक असमिकाएँ x + y > 4, 2x – y > 0,
(i) रेखा x + y = 4, बिन्दु (4, 0) और (0, 4) से होकर जाती है। +
अब x + y > 4 में x = 0 y = 0 रखने पर, हमें प्राप्त हुआ 0 > 4 जो सत्य नहीं है।
∴ मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है।
x + y >4 का हल वे सब बिन्दु हैं जो रेखा AB के ऊपर है।

(ii) रेखा 2x – y = 0, बिन्दु 0 (0, 0) और D(1, 2) से होकर जाती है।
2x – y > 0 में x = 1, y = 0 रखते हुए 2 > 0, जो सत्य है।
∴ बिन्दु P(1, 0), 2x – y > 0 के क्षेत्र में है।
∴ 2x – y > 0 का हल वे सब बिन्दु हैं जो OD के नीचे हैं।
प्रश्न 5.
2x – y > 1,x – 2y < – 1. हल: दी हुई रैखिक असमिकाएँ 2x – y > 1 और x – 2y < – 1 (i) सरल रेखा 2x – y = 1 बिन्दु (12,0) और (0, – 1) से होकर जाती है। 2x – y > 1 में x = 0, y = 0 रखने पर 0 > 1, यह सत्य नहीं है।
∴ मूल बिन्दु (0, 0), 2x – y > 1 के क्षेत्र में नहीं है।
⇒ 2x – y > 1 का हल वे सब बिन्दु हैं जो रेखा AB के नीचे है।

(ii) रेखा x – 2y = – 1 बिन्दु C(-1, 0) और D(0,1/2) से होकर जाती है।
x – 2y < – 1 में x = 0, y = 0 रखने पर 0 < – 1, यह सत्य नहीं है। ∴ मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है। ⇒ 2x – y > 1 और x – 2y < – 1 का हल वह उभयनिष्ठ भाग QPR है जो AB के नीचे और CD के ऊपर है।
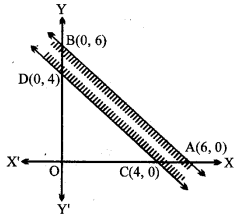
प्रश्न 6. x + y ≤ 6, x + y ≥ 4. हल: दी हुई रैखिक असमिकाएँ x + y ≤ 6 और x + y ≥ 4 है। (i) रेखा x + y = 6, बिन्दु A(6, 0), B(0, 6) से होकर जाती है। x + y ≤ 6 में x = 0, y = 0 रखने पर 0 + 0 ≤ 6 अर्थात् 0 ≤ 6 जो सत्य है ∴ मूल बिन्दु (0, 0), x + y ≤ 6 के क्षेत्र में है। (ii) रेखा x + y = 4, बिन्दु C(4, 0) और D(0, 4) से होकर जाती है। x + y ≥ 4 में x = 0, y = 0 रखने पर, 0 ≥ 4, यह सत्य नहीं है। ∴ मूल बिन्दु (0, 0) x + y ≥ 4 में नहीं है। इसका हल वे सब बिन्दु हैं जो CD के ऊपर है। दी हुई आकृति में छायांकित क्षेत्र x + y ≤ 6 और x + y ≥ 4 के हल को दर्शाता है।
प्रश्न 7. 2x + y ≥ 8, x + 2y ≥ 10. हल: दी हुई रैखिक असमिकाएँ 2x + y ≥ 8, x + 2y ≥ 10 (i) रेखा 2x + y = 8 बिन्दु A(4,0); B(0, 8) से होकर जाती है। 2x + y ≥ 8 में x = 0, y = 0 रखने पर 0 ≥ 8 जो असत्य है। ∴ मूल बिन्दु (0, 0) इसके क्षेत्र में नहीं है। ⇒ 2x + y ≥ 8 का हल वे सब बिन्दु हैं जो रेखा AB के ऊपर है।

(ii) रेखा x + 2y = 10, बिन्दु C(10, 0) और D(0, 5) से होकर जाती है। x + 2y ≥ 10 में x = 0, y = 0 रखने पर, 0 ≥ 10, यह सत्य नहीं है। ∴ मूल बिन्दु (0, 0) x + 2y ≥ 10 में नहीं है। ⇒ x + 2y ≥ के सभी बिन्दु CD के ऊपर हैं। अर्थात् 2x + y ≥ 8, x + 2y ≥ 10 का हल छायांकित उभयनिष्ठ भाग BPC है। प्रश्न 8. x + y ≤ 9, y ≥ x, x ≥ 0. हल: दी हुई रैखिक असमिकाएँ x + y ≤ 9, y ≥ x, x ≥ 0 (i) सरल रेखा x + y = 9 बिन्दु A(9, 0) और B(0, 9) से होकर जाती है। x + y ≤ 9 में x = 0, y = 0 रखते हुए 0 + 0 ≤ 9 अर्थात् 0 ≤ 9 जो सत्य है। ∴ मूल बिन्दु (0, 0) इसके क्षेत्र में है। ⇒ x + y ≤ 9 के बिन्दु AB रेखा के नीचे हैं। (ii) सरल रेखा y = x बिन्दु O(0, 0) और C(3, 3) से होकर जाती है। y > x में x = 0, y = 3 रखने पर, 3 > 0 जो सत्य है।
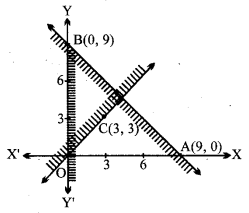
∴ बिन्दु (3, 0) इसके क्षेत्र में है।
⇒ y > x के सभी बिन्दु y = x के ऊपर हैं।
(iii) सरल रेखा x = 0, y- अक्ष को निरूपित करती है।
x ≥ 0 में x = 3, y = 0 रखने पर 3 ≥ 0 जो सत्य है।
⇒ x ≥ 0 के सभी बिन्दु x = 0 के दाईं ओर है।
आकृति में उभयनिष्ठ छायांकित क्षेत्र असमिकाओं x + y ≥ 9, y > x, x ≥ 0 का हल है।
प्रश्न 9.
5x + 4y ≤ 20,x ≥ 1,y ≥ 2.
हल:
दी हुई रैखिक असमिकाएँ 5x + 4y ≤ 20, x ≥ 1,y ≥ 2
सरल रेखा 5x + 4y = 20 बिन्दु A (4,0) और B (0, 5) से होकर जाती हैं। 5x + 4y ≤ 20 में x = 0, y = 0 रखने पर, 0 + 0 ≤ 20 अर्थात् 0 ≤ 20 जो सत्य है।
∴ मूल बिन्दु (0, 0) इसके क्षेत्र में है।
5x + 4y ≤ 20 के सभी बिन्दु रेखा AB के नीचे है।

(ii) x = 1 बिन्दु C(1 , 0), D(1, 2) से होकर जाती है।
x ≥ 1 में x = 0 रखने पर 0 ≥ 1 जो सत्य नहीं है।
∴ x ≥ 1 के सभी बिन्दु x = 1 के दायीं ओर होते हैं।
(iii) y = 2, बिन्दु E(0, 2) और F(4, 2) से होकर जाती है।
y ≥ 2 में y = 0. रखने पर 0 ≥ 2 सत्य नहीं है।
∴ मूल बिन्दु इसके क्षेत्र में नहीं है।
y ≥ 2 का हल वे सब बिन्दु हैं जो EF के ऊपर हैं।
दी हुई असमिकाओं का हल आकृति में उभयनिष्ठ PDR छायांकित क्षेत्र द्वारा दर्शाया गया है।
प्रश्न 10.
3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0.
हल:
दी हुई असमिकाएँ : 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0.
(i) रेखा 3x + 4y = 60 बिन्दु A(20, 0) तथा B(0, 15) से होकर जाती है।
असमिका 3x + 4y ≤ 60 में x = 0, y = 0 रखने पर 0 < 60 जो सत्य है। मूल बिन्दु इस क्षेत्र में पड़ता है। ⇒ इस असमिका का हल वे सब बिन्दु हैं जो AB के नीचे हैं।
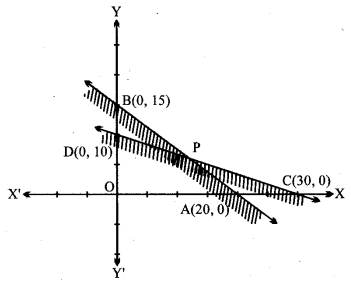
(ii) रेखा x + 3y = 30 बिन्दु C(30, 0) और D(0, 10) से होकर जाती है।, असमिका x + 3y ≤ 30 में x = 0, y = 0 रखने पर 0 ≤ 30 जो सत्य है। मूल बिन्दु इसके क्षेत्र में है। इसका हल वे सब बिन्दु हैं जो CD के नीचे हैं। (iii) x = 0, y-अक्ष को निरुपित करती है। x ≥ 0 में वे सब बिन्दु हैं जो y-अक्ष की दाईं ओर हैं। (iv) y = 0, x-अक्ष को निरुपित करती है। और y > 0 में वे सब बिन्दु हैं जो x-अक्ष के ऊपर हैं दी हुई असमिका का हल वे सब बिन्दु हैं जो उभयनिष्ठ क्षेत्र PDOA में आते हैं।
प्रश्न 11.
2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6.
हल:
दी हुई असमिकाएँ 2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
(i) रेखा 2x + y = 4, बिन्दु A (2, 0) और B(0, 4) से होकर जाती है।
असमिका 2x + y ≥ 4 में x = 0, y = 0 रखने पर 0 + 0 ≥ 4 अर्थात् 0 ≥ 4जो सत्य नहीं है। मूल बिन्दु इस क्षेत्र में नहीं है।
इसका हल वे सब बिन्दु हैं जो AB के ऊपर हैं।

(ii) रेखा x + 3y = 3 बिन्दु C(3, 0), D(0, 10) से होकर जाती है।
असमिका x + 3y ≤ 3 में x = 0, y = 0 रखने पर 0 ≤ 3 जो सत्य है।
मूल बिन्दु इसके क्षेत्र में है। इसका हल वे सब बिन्दु हैं जो CD के नीचे हैं
(iii) रेखा 2x – 3y = 6, बिन्दु C(3,0) और E(0, – 2) से होकर जाती है।
असमिका 2x – 3y ≤ 6 में x = 0, y = 0 रखने पर 0 ≤ 6, जो सत्य है।
मूल बिन्दु इसके क्षेत्र में है। इसका हल वे सब बिन्दु हैं जो CE के ऊपर हैं।
दी हुई असमिकाओं का हल छायांकित उभयनिष्ठ क्षेत्र AQC के सब बिन्दु हैं।
प्रश्न 12.
x – 3y ≤ 3, 3x + 4y 12, x ≥ 0, y ≥ 1.
हल:
दी हुई असमिकाएँ x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0,y ≥ 1
(i) रेखा x – 3y = 3 बिन्दु A(3, 0), B(0, – 1) से होकर जाती है।
असमिका x – 3y ≤ 3 में x = 0, y = 0 रखने पर, 0 ≤ 3 जो सत्य है।

∴ मूल बिन्दु इसके क्षेत्र में है।
इसका हल वे सब बिन्दु हैं जो AB के ऊपर है।
(ii) रेखा 3x + 4y = 12 बिन्दु C(4, 0) और D(0, 3) से होकर जाती है।
असमिका 3x + 4y ≥ 12 में x = 0, y = 0 रखने पर 0 ≥ 12, जो सत्य नहीं है। मूल बिन्दु इसके क्षेत्र में नहीं है।
⇒ इसका हल वे सब बिन्दु हैं जो CD के ऊपर है।
(iii) x = 0, y-अक्ष को दर्शाती है।
x ≥ 0 का हल वे सब बिन्दु हैं जो y-अक्ष के दाईं ओर है।
(iv) रेखा y = 1 बिन्दु E(0, 1), Q(3, 1) से होकर जाती है।
असमिका y ≥ 1 का हल वे सब बिन्दु है जो संख्या y = 1 पर पड़ते हैं या इसके ऊपर हैं।
दी हुई असमिकाओं का हल वे सब बिन्दु हैं जो उभयनिष्ठ क्षेत्र PDQRS से निरूपित किया गया है।
प्रश्न 13.
4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0.
हल:
दी हुई असमिकाएँ 4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
(i) सरल रेखा 4x + 3y = 60 बिन्दु A(15, 0), B(0, 20) से होकर जाती है।
4x + 3y ≤ 60 में x = 0, y = 0 रखने पर 0 ≤ 60 जो सत्य है।
∴ मूल बिन्दु इसके क्षेत्र में है।
⇒ इस असमिका का हल वे बिन्दु हैं जो रेखा AB या AB के नीचे होते हैं।

(ii) y – 2x = 0, बिन्दु 0(0, 0) और C(5, 10) से होकर जाती है।
y – 2x ≥ 0 में x = 5, y = 0 रखने पर, 0 – 10 ≥ 0 अर्थात् -10 ≥ 0 जो सत्य नहीं है।
बिन्दु (5, 0) इसके क्षेत्र में नहीं है।
⇒ y – 2x ≥ 0 का हल वे सब बिन्दु हैं जो OC पर और OC के ऊपर हैं।
(iii) रेखा x ≥ 3 बिन्दु D(3, 0), E(3, 10) से होकर जाती है।
असमिका x ≥ 3 के हल वे बिन्दु हैं जो DE या.DE के दाईं ओर हैं।
(iv) x ≥ 0, y ≥ 0 पहले चतुर्थांश के बिन्दु हैं।
दी हुई असमिकाओं का हल उभयनिष्ठ क्षेत्र PQR पर और उसके अन्दर के बिन्दु हैं।
प्रश्न 14.
3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0.
हल:
दी हुई असमिकाएँ 3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0
(i) सरल रेखा 3x + 2y = 150, बिन्दु A(50, 0), B(0, 75) से होकर जाती है। असमिका 3x + 2y ≤ 150 में x = 0, y = 0 रखने पर 0 ≤ 150 जो सत्य है।
∴ मूल बिन्दु इसके क्षेत्र में है।
⇒ इसका हल वे सब बिन्दु हैं जो AB पर या AB से नीचे हैं।
image 14
(ii) रेखा x + 4y = 80 बिन्दु C(80, 0), D(0, 20) से होकर जाती है।
असमिका x + 4y ≤ 80 में x = 0, y = 0 रखने पर 0 ≤ 80 जो सत्य है।
∴ मूल बिन्दु इस क्षेत्र में है।
इसका हल वे सब बिन्दु हैं जो CD पर या CD के नीचे स्थित है।
(iii) x = 15 रेखा y-अक्ष के समान्तर है और x ≤ 15 का हल वे बिन्दु हैं जोx = 15 पर या इसके बाईं ओर स्थित है।
(iv) y ≥ 0 में y-अक्ष पर और उसके ऊपर के सब बिन्दु हैं।
दी हुई असमिकाओं का हल उभयनिष्ठ क्षेत्र PQRS हैं।
प्रश्न 15.
x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0.
हल:
दी हुई सममिकाएँ x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0

(i) सरल रेखा x + 2y = 10 बिन्दु A(10, 0) और B(0, 5) से होकर जाती है।
असमिका x + 2y ≤ 10 में x = 0, y = 0 रखने पर 0 ≤ 10 जो सत्य है।
∴ मूल बिन्दु इसके क्षेत्र में है।
इस असमिका का हल वे सब बिन्दु हैं जो AB पर हैं तथा AB के नीचे हैं।
(ii) रेखा x + y = 1 बिन्दु C(1, 0), D(0 , 1) से होकर जाती है।
असमिका x + y ≥ 1 में x = 0, y = 0 रखने पर, 0 ≥ 1 जो सत्य नहीं है।
⇒ मूल बिन्दु इसके क्षेत्र में नहीं है।
⇒ इस असमिका का हल वे सब बिन्दु हैं जो CD पर हैं या इसके ऊपर हैं।
(iii) रेखा x – y = 0 बिन्दु (0, 0) और (1, 1) से होकर जाती है। असमिका x – y ≤ 0 में x = 0, y = 0 रखने पर 0 ≤ 0 जो सत्य है।
(0, 0) इसके क्षेत्र में है।
⇒ इस असमिका का हल वे बिन्दु जो x – y = 0 पर हैं या इसके ऊपर हैं।
(iv) x ≥ 0 वह क्षेत्र है जो y-अक्ष के दाईं ओर है।
(v) y ≥ 0 वह क्षेत्र है जो x-अक्ष के ऊपर है।
दी हुई असमिकाओं का हल वे सब बिन्दु हैं जो उभयनिष्ठ क्षेत्र PQDB में है।