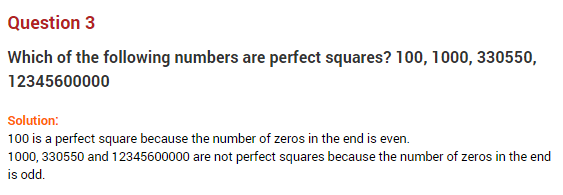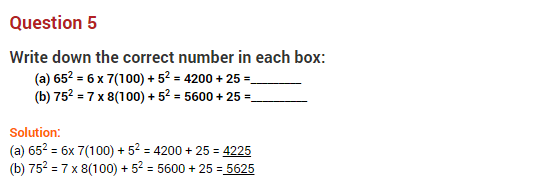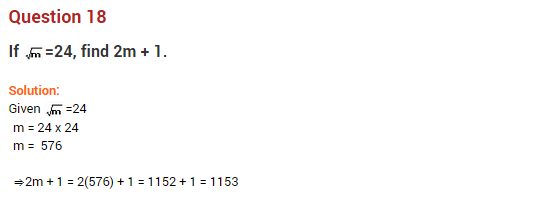Chapter 6 Squares and Square Roots

Chapter 6 Squares and Square Roots

Very Short Answer Type

Question 1.
Find the perfect square numbers between 40 and 50.
Solution:
Perfect square numbers between 40 and 50 = 49.

Question 2.
Which of the following 24², 49², 77², 131² or 189² end with digit 1?
Solution:
Only 49², 131² and 189² end with digit 1.

Question 3.
Find the value of each of the following without calculating squares.

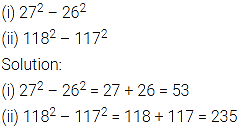
Question 4.
Write each of the following numbers as difference of the square of two consecutive natural numbers.
(i) 49
(ii) 75
(iii) 125
Solution:

Question 5.
Write down the following as sum of odd numbers.
(i)
(ii)
Solution:
(i)  = Sum of first 7 odd numbers = 1 + 3 + 5 + 7 + 9 + 11 + 13
(ii)  = Sum of first 9 odd numbers = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17

Question 6.
Express the following as the sum of two consecutive integers.
(i)
(ii)
Solution:

Question 7.
Find the product of the following:
(i) 23 × 25
(ii) 41 × 43
Solution:
(i) 23 × 25 = (24 – 1) (24 + 1) = 2 – 1 = 576 – 1 = 575
(ii) 41 × 43 = (42 – 1) (42 + 1) = 4 – 1 = 1764 – 1 = 1763

Question 8.
Find the squares of:

Solution:

Short Answer Type

Question 11.
Using the prime factorisation method, find which of the following numbers are not perfect squares.
(i) 768
(ii) 1296
Solution:


Here, 3 is not in pair.
768 is not a perfect square.


Here, there is no number left to make a pair.
1296 is a perfect square.

Question 12.
Which of the following triplets are Pythagorean?
(i) (14, 48, 50)
(ii) (18, 79, 82)
Solution:

Question 13.
Find the square root of the following using successive subtraction of odd numbers starting from 1.
(i) 169
(ii) 81
(iii) 225
Solution:
(i) 169 – 1 = 168, 168 – 3 = 165, 165 – 5 = 160, 160 – 7 = 153, 153 – 9 = 144, 144 – 11 = 133, 133 – 13 = 120, 120 – 15 = 105, 105 – 17 = 88, 88 – 19 = 69,
69 – 21 = 48, 48 – 23 = 25, 25 – 25 = 0
We have subtracted odd numbers 13 times to get 0.
√169 = 13
(ii) 81 – 1 = 80, 80 – 3 = 77, 77 – 5 = 72, 72 – 7 = 65, 65 – 9 = 56, 56 – 11 = 45, 45 – 13 = 32, 32 – 15 = 17, 17 – 17 = 0
We have subtracted 9 times to get 0.
√81 = 9
(iii) 225 – 1 = 224, 224 – 3 = 221, 221 – 5 = 216, 216 – 7 = 209, 209 – 9 = 200, 200 – 11 = 189, 189 – 13 = 176, 176 – 15 = 161, 161 – 17 = 144, 144 – 19 = 125,
125 – 21 = 104, 104 – 23 = 81, 81 – 25 = 56, 56 – 27 = 29, 29 – 29 = 0
We have subtracted 15 times to get 0.
√225 = 15

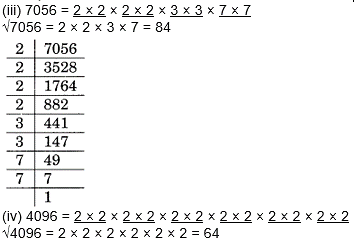
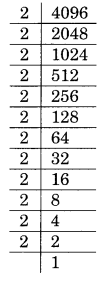
Question 16.
Find the square roots of the following decimal numbers
(i) 1056.25
(ii) 10020.01
Solution:

Question 17.
What is the least number that must be subtracted from 3793 so as to get a perfect square? Also, find the square root of the number so obtained.
Solution:
First, we find the square root of 3793 by division method.

Here, we get a remainder 72
6 < 3793
Required perfect square number = 3793 – 72 = 3721 and √3721 = 61

Question 18.
Fill in the blanks:
(а) The perfect square number between 60 and 70 is …………
(b) The square root of 361 ends with digit …………..
(c) The sum of first n odd numbers is …………
(d) The number of digits in the square root of 4096 is ………..
(e) If (-3 = 9, then the square root of 9 is ……….
(f) Number of digits in the square root of 1002001 is …………

Question 19.
Simplify: √900 + √0.09 + √0.000009
Solution:
We know that √(ab) = √a × √b
√900 = √(9 × 100) = √9 × √100 = 3 × 10 = 30
√0.09 = √(0.3 × 0.3) = 0.3
√0.000009 = √(0.003 × 0.003) = 0.003
√900 + √0.09 + √0.000009 = 30 + 0.3 + 0.003 = 30.303

Higher Order Thinking Skills (HOTS)

Question 20.
Find the value of x if

Solution:

Question 21.
Simplify:

Solution:

Question 22.
A ladder 10 m long rests against a vertical wall. If the foot of the ladder is 6 m away from the wall and the ladder just reaches the top of the wall, how high is the wall? (NCERT Exemplar)

Solution:
Let AC be the ladder.
Therefore, AC = 10 m
Let BC be the distance between the foot of the ladder and the wall.
Therefore, BC = 6 m
∆ABC forms a right-angled triangle, right angled at B.
By Pythagoras theorem,

Question 23.
Find the length of a diagonal of a rectangle with dimensions 20 m by 15 m. (NCERT Exemplar)
Solution:
Using Pythagoras theorem, we have Length of diagonal of the rectangle =  units

Hence, the length of the diagonal is 25 m.

Question 24.
The area of a rectangular field whose length is twice its breadth is 2450 m2. Find the perimeter of the field.
Solution:
Let the breadth of the field be x metres. The length of the field 2x metres.
Therefore, area of the rectangular field = length × breadth = (2x)(x) = (2x²) m²
Given that area is 2450 .
Therefore, 2 = 2450
⇒  = 1225
⇒ x = √1225 or x = 35 m
Hence, breadth = 35 m
and length = 35 × 2 = 70 m
Perimeter of the field = 2 (l + b ) = 2(70 + 35) m = 2 × 105 m = 210 m.