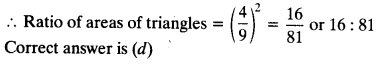Chapter 6 Triangles Ex 6.4

Chapter 6 Triangles Ex 6.4

Question 1.
Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Solution:
Since, ∆ABC ~ ∆DEF
The ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding sides.

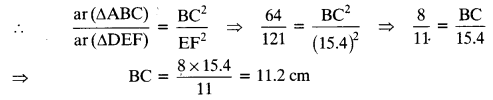
Question 2.
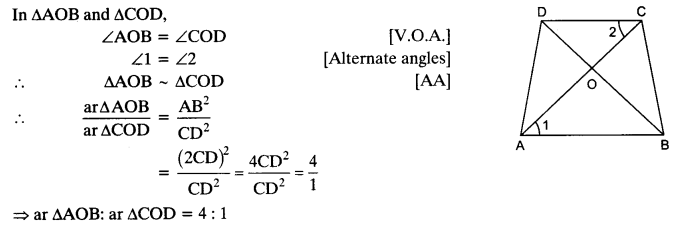
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Solution:
ABCD is a trapezium with AB || DC and AB = 2 CD

Question 3.
In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that


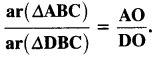
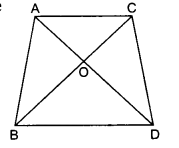
Solution:

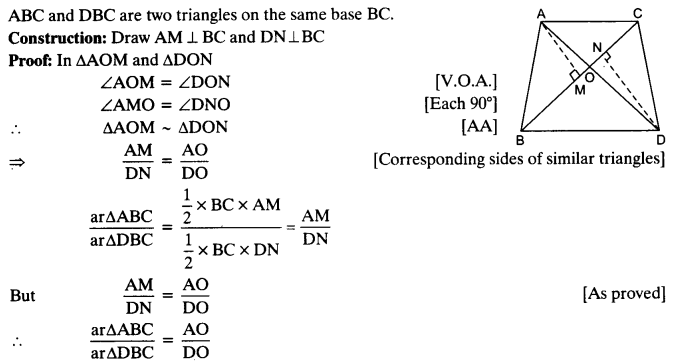
Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution:

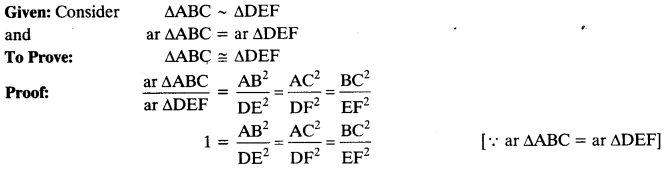
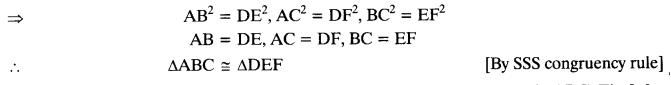
Question 5.
D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
Solution:

Question 6.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:

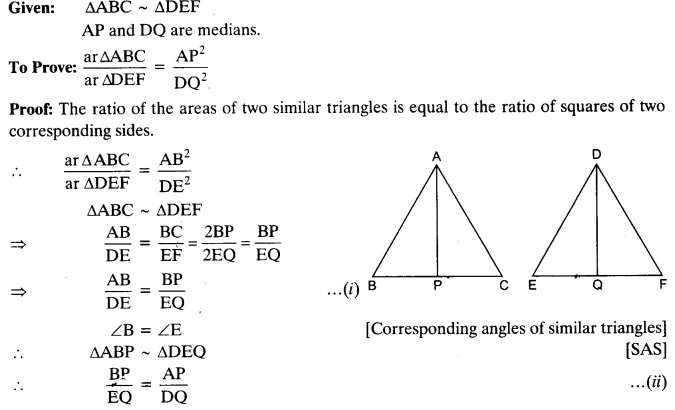
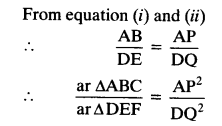
Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:

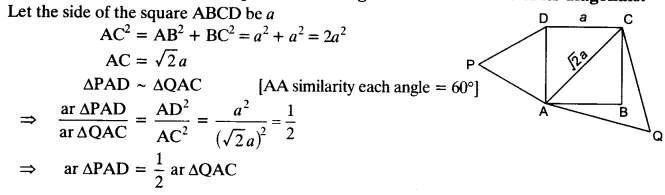
Question 8.
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(a) 2 :1
(b) 1:2
(c) 4 :1
(d) 1:4
Solution:

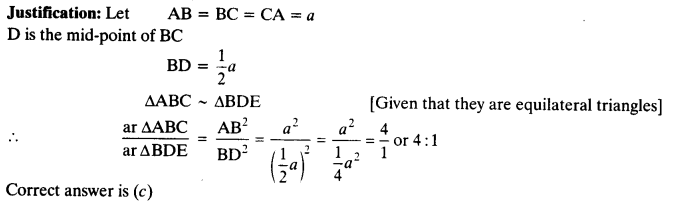
Question 9.
Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
(a) 2:3
(b) 4:9
(c) 81:16
(d) 16:81
Solution:
Justification: Areas of two similar triangles are in the ratio of the squares of their corresponding sides.