Chapter 7 घन और घनमूल Ex 7.1
प्रश्न 1.
निम्नलिखित में से कौन-सी संख्याएँ पूर्ण घन – नहीं हैं?
- 216
- 128
- 1000
- 100
- 46656
हल:
1. 216 = 2 x 2 x 2 x 3 x 3 x 3
स्पष्ट है कि अभाज्य गुणनखण्ड समान गुणनखण्डों के त्रिक हैं और कोई गुणनखण्ड शेष नहीं है।
अत: 216 एक पूर्ण घन है।
2. 128 = 2 x 2 x 2 x 2 x 2 x 2 x 2
यहाँ अभाज्य गुणनखण्डों के त्रिक बनाने पर 2 शेष रहता है।
अतः 128 एक पूर्ण घन नहीं है।
3. 1000 = 2 x 2 x 2 x 5 x 5 x 5
स्पष्ट है कि अभाज्य गुणनखण्ड समान गुणनखण्डों के त्रिक हैं और कोई गुणनखण्ड शेष नहीं है।
अतः 1000 एक पूर्ण घन है।
4. 100 = 2 x 2 x 5 x 5
स्पष्ट है कि अभाज्य गुणनखण्ड समान गुणनखण्डों के त्रिक नहीं हैं तथा 2 x 2 x 5 x 5 शेष रहता है।
अतः 100 पूर्ण घन नहीं है।
5. 46656 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3 x 3
स्पष्ट है कि अभाज्य गुणनखण्ड समान गुणनखण्डों के त्रिक हैं तथा कोई गुणनखण्ड शेष नहीं है।
अतः 46656 एक पूर्ण घन संख्या है।
प्रश्न 2.
वह सबसे छोटी संख्या ज्ञात कीजिए जिसमें निम्नलिखित संख्याओं को गुणा करने पर पूर्ण घन बन जाए:
- 243
- 256
- 72
- 675
- 100.
हल:
1.

243 के अभाज्य गुणनखण्ड करने पर, 243 = 3 x 3 x 3 x 3 x 3
यहाँ अभाज्य गुणनखण्डों के तीन-तीन का समूह बनाने पर 3 के समूह का एक गुणनखण्ड कम है।
अतः 3 से गुणा करने पर संख्या 243 पूर्ण घन बन जाएगी।
2.

256 के अभाज्य गुणनखण्ड करने पर, 256 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
यहाँ अभाज्य गुणनखण्डों के तीन-तीन का समूह बनाने पर 2 के समूह का एक गुणनखण्ड कम है।
अतः 2 से गुणा करने पर संख्या 256 पूर्ण घन बन जाएगी।
3.

72 के अभाज्य गुणनखण्ड करने पर, 72 = 2 x 2 x 2 x 3 x 3
यहाँ अभाज्य गुणनखण्डों के तीन-तीन का समूह बनाने पर 3 के समूह का एक गुणनखण्ड कम है।
अतः 3 से गुणा करने पर संख्या 72 पूर्ण घन बन जाएगी।
4.

675 के अभाज्य गुणनखण्ड करने पर, 675 = 3 x 3 x 3 x 5 x 5
यहाँ अभाज्य गुणनखण्डों के तीन-तीन के समूह बनाने पर 5 के समूह का एक गुणनखण्ड कम है।
अतः 5 से गुणा करने पर संख्या 675 पूर्ण घन बन जाएगी।
5.

100 के अभाज्य गुणनखण्ड करने पर, 100 = 2 x 2 x 5 x 5
यहाँ अभाज्य गुणनखण्डों के तीन-तीन के समूह बनाने पर 2 के समूह का एक व 5 के समूह का एक गुणनखण्ड कम है।
अत: 2 x 5 = 10 से गुणा करने पर संख्या 100 पूर्ण घन बन जाएगी।
प्रश्न 3.
वह सबसे छोटी संख्या ज्ञात कीजिए जिससे निम्नलिखित संख्याओं को भाग देने पर भागफल एक पूर्ण घन प्राप्त हो जाए
- 81
- 128
- 135
- 192
- 704.
हल:
1.
![]()
81 = 3 x 3 x 3 x 3
यहाँ अभाज्य गुणनखण्डों की तीन-तीन के समूह (त्रिक) बनाने पर गुणनखण्ड 3 अधिक है।
अत: 3 से भाग देने पर संख्या 81 पूर्ण घन बन जाएगी।
2.

128 = 2 x 2 x 2 x 2 x 2 x 2 x 2
यहाँ अभाज्य गुणनखण्डों के तीन-तीन के समूह (त्रिक) बनाने पर गुणनखण्ड 2 अधिक है।
अतः 2 से भाग देने पर संख्या 128 पूर्ण घन बन जाएगी।
3.
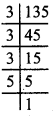
135 = 3 x 3 x 3 x 5
यहाँ अभाज्य गुणनखण्डों के तीन-तीन के समूह (त्रिक) बनाने पर गुणनखण्ड 5 अधिक है।
अत: 5 से भाग करने पर संख्या 135 पूर्ण घन बन जाएगी।
4.

192 = 2 x 2 x 2 x 2 x 2 x 2 x 3
यहाँ अभाज्य गुणनखण्डों के तीन-तीन के समूह (त्रिक) बनाने पर गुणनखण्ड 3 अधिक है।
अतः 3 से भाग करने पर संख्या 192 पूर्ण घन बन जाएगी।
5.

704 = 2 x 2 x 2 x 2 x 2 x 2 x 11
यहाँ अभाज्य गुणनखण्डों के तीन-तीन के समूह त्रिक बनाने पर गुणनखण्ड 11 अधिक है।
अतः 11 से भाग देने पर संख्या 704 पूर्ण घन बन जाएगी।
प्रश्न 4.
परीक्षित प्लास्टिसिन का एक घनाभ बनाता है जिसकी भुजाएँ 5 cm, 2 cm और 5 cm हैं। एक घन बनाने के लिए ऐसे कितने घनाभों की आवश्यकता होगी?
हल:
घनाभ का आयतन = लम्बाई x चौड़ाई x ऊँचाई
5 x 2 x 5 सेमी3 = 2 x 5 x 5 सेमी3 घन बनाने के लिए आवश्यक घनाभों की संख्या
= 2 x 2 x 5 = 20 घनाभ
पाठ्य-पुस्तक पृष्ठ संख्या # 122
घनमूल
प्रश्न 1.
यदि किसी घन का आयतन 125 cm है, तो उसकी भुजा की लम्बाई क्या होगी?
हल:
घन का आयतन = 125 घन सेमी
घन की भुजा =
= 5 सेमी
पाठ्य-पुस्तक पृष्ठ संख्या # 123
सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 7.2)
प्रश्न 1.
बताइए कि सत्य है या असत्य: किसी पूर्णांक m के लिए, m2 < m3 होता है। क्यों?
हल:
1. माना कि यदि m = 2, तब
m2 = 2 x 2 = 4 तथा m3 = 2 x 2 x 2 = 8
स्पष्ट है कि 4 < 8 अर्थात् m2 < m3
2. यदि m = 3, तब
m2 = 3 x 3 = 9 तथा m3 = 3 x 3 x 3 = 27
स्पष्ट है कि 9 < 27 अर्थात् m2 < m3
3. यदि m = 4, तब
m2 = 4 x 4 = 16 तथा m3 = 4 x 4 x 4 = 64
स्पष्ट है कि 16 < 64 अर्थात् m2 < m3
4. यदि m = 5, तब
m2 = 5 x 5 = 25 तथा m2 = 5 x 5 x 5= 125
स्पष्ट है कि 25 < 125 अर्थात् m2 < m3
5. परन्तु यदि m = 1, तब
m2 = 1 x 1 = 1 तथा m3 = 1 x 1 x 1 = 1
स्पष्ट है कि m2 = m3
6. यदि m = – 1, तब
m2 = (-1) x (-1) = 1
तथा m3 = (-1) x (-1) x (-1) = – 1
स्पष्ट है कि, 1 > – 1 अर्थात् m2 > m3
7. यदि m = -2, तब
m2 = (-2) x (-2) = 4
तथा m3 = (-2) (-2) (-2) = – 8
स्पष्ट है कि 4 > – 8 अर्थात् m2 > m3
8. यदि m = – 3, तब
m2 = (-3) x (-3)= 9
तथा m3 = (-3) (-3) (-3) = – 27
स्पष्ट है कि 9 > (-27) अर्थात् m2 > m3
9. परन्तु यदि m = 0, तब
m2 = 0 तथा m3 = 0
∴ m2 = m3
अतः हम कह सकते हैं कि ऋणात्मक पूर्णांक m के लिए m2 < m3 असत्य है।