Chapter 7 त्रिभुज Ex 7.2
प्रश्न 1.
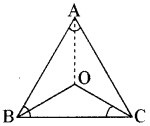
एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिन्दु 0 पर प्रतिच्छेद करते हैं। A और O को जोड़िए। दर्शाइए कि
(i) OB = OC
(ii) AO कोण A को समद्विभाजित करता है।
हल:
(i) ∆ABC में,
AB = AC
या B = ∠C
चूँकि बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।
या ∠OBC = ∠OCB …..(i)
∵ OB तथा OC क्रमशः ∠B तथा ∠C को दो भागों में विभाजित करते हैं

या OB = OC …(ii) समान कोणों की सम्मुख भुजायें समान होती हैं। (इति सिद्धम् )
(ii) अब ∆ABO तथा ∆ACO में
AB = AC [दिया है]
∠ABO = ∠ACO समीकरण (i) से
OB = OC समीकरण (ii) से
∴ SAS सर्वांगसमता गुण से
∆ABO ≅ ∆ACO
या BAO = ∠CAO [सर्वांगसम त्रिभुजों के संगत भाग]
या AO, ∠BAC को समद्विभाजित करता है। (इति सिद्धम् )
प्रश्न 2.
∆ABC में AD भुजा BC का लम्ब समद्विभाजक है ( देखिए आकृति)। दर्शाइए कि ∆ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC

हल:
प्रश्न में दी गई आकृति के ∆ABD और ∆ACD में
∠ADB = ∠ADC = 90° (प्रत्येक) [क्योंकि AD ⊥ BC (दिया है)]
BD = CD [∵ AD, BC को समद्विभाजित करती है (दिया है)]
तथा AD = AD (उभयनिष्ठ भुजाएँ)
∴ ∆ADB = ∆ACD (सर्वांगसमता के SAS नियम से)
⇒ AB = AC [∵ ये सर्वांगसम त्रिभुजों के संगत भाग]
अत: ABC एक समद्विबाहु त्रिभुज है।
प्रश्न 3.
ABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमशः शीर्षलम्ब BE और CF खींचे गए हैं ( देखिए आकृति)। दर्शाइए कि ये शीर्षलम्ब बराबर हैं।

हल:
प्रश्न में दी गई आकृति के त्रिभुजों ∆ABE और ∆ACF में
∠A = ∠A (उभयनिष्ठ कोण)
∠AEB = ∠AFC = 90° (प्रत्येक) (दिया है)
तथा AB = AC (दिया है)
∴ ∆ABE ≅ ∆ACF (सर्वांगसमता के नियम AAS से)
BE = CF [क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग]
अर्थात् यह कहा जा सकता है कि समान भुजाओं पर खींचे गए शीर्ष लम्ब समान होते हैं।
प्रश्न 4.
ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलम्ब BE और CF बराबर हैं ( देखिए आकृति)। दर्शाइए कि

(i) ∆ABE ≅ ∆ACF
(ii) AB = AC, अर्थात् ∆ABC एक समद्विबाहु त्रिभुज है।
हल:
प्रश्नानुसार दिए गए चित्र में ∆ABE और ∆ACF में
∠A = ∠A (उभयनिष्ठ कोण)
∠AEB = ∠AEC (प्रत्येक कोण 90°)
[क्योंकि BE ⊥ AC और CF ⊥ AB (दिया है)]
तथा BE = CF (दिया है)
(i) ∴ ∆ABE ≅ ∆ACF [सर्वांगसमता के AAS नियम के अनुसार]
(ii) अतः AB = AC [सर्वांगसमता त्रिभुजों के संगत भाग हैं]
अर्थात् ∆ABC एक समद्विबाहु त्रिभुज है।
प्रश्न 5.
ABC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं ( देखिए आकृति)। दर्शाइए कि ∠ABD = ∠ACD है।

हल:
प्रश्नानुसार दिए गए चित्र के समद्विबाहु ∆ABC में
∴ ∠ACB = ∠ABC …..(i) [क्योंकि ये समान भुजाओं के सम्मुख कोण हैं]
AB = AC (दिया है) साथ ही पुनः समद्विबाहु त्रिभुज BCD में
∴ ∠BCD = ∠CBD …..(ii) [क्योंकि ये समान भुजाओं के सम्मुख कोण हैं]
तथा BD = DC समीकरण (i) व (ii) के संगत पक्षों को जोड़ने पर
∠ACB + ∠BCD = ∠ABC + ∠CBD
या ∠ACD = ∠ABD
या ∠ABD = ∠ACD(इति सिद्धम्)
प्रश्न 6.
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिन्दु D तक इस प्रकार बढ़ाई गई है कि AD = AB है ( देखिए आकृति)। दर्शाइए कि ∠BCD एक समकोण है।
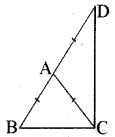
हल:
चित्रानुसार दिए गए समद्विबाहु त्रिभुज ABC में
∠ACB = ∠ABC [क्योंकि ये समान भुजाओं के सम्मुख कोण हैं।]
AB = AC (दिया है) अब AD = AB (रचना से)
परन्तु AB = AC (दिया है)
∴ AD = AB = AC
⇒ AD = AC
अब त्रिभुज ADC में AD = AC
तथा ∠ADC = ∠ACD …..(ii)
[क्योंकि ये ∆ADC में समान भुजाओं के सम्मुख कोण हैं]
तथा ∠BAC + ∠CAD = 180° ……(iii)
(रैखिक युग्म अभिगृहीत से)
∴ हम जानते हैं कि त्रिभुज का बहिष्कोण अंत:सम्मुख कोणों के योगफल के बराबर होता है।
∴ त्रिभुज ABC से ∠CAD = ∠ABC + ∠ACB
= ∠ACB + ∠ACB [समीकरण (i) से]
∠CAD = 2 ∠ACB …..(iv)
इसी प्रकार पुनः ∆ADC से
∠BAC = ∠ACD + ∠ADC क्योंकि हम जानते हैं कि त्रिभुज का बहिष्कोण अंतःसम्मुख कोणों के योगफल के बराबर होता है।
अतः ∠BAC = ∠ACD + ∠ACD [समीकरण (ii) से]
या ∠BAC = 2∠ACD …..(v)
अब समीकरण (iii), (iv) व (i) से
2∠ACB + 2∠ACD = 180°
या 2 (∠ACB + ∠ACD) = 180°
या ∠ACB + ∠ACD = 90°
या ∠BCD = 90°
अतः ∠BCD एक समकोण है।
प्रश्न 7.
ABC एक समकोण त्रिभुज है जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
हल:
प्रश्नानुसार एक समकोण त्रिभुज ABC है जिसमें
∠A = 90°
तथा AB = AC
∆ABC में AB = AC
अर्थात् ∠C = ∠B …..(i) [क्योंकि ये समान भुजाओं के सम्मुख कोण हैं।]

अब पुन: ∆ABC में ∠A + ∠B + ∠C = 180°
(त्रिभुज के कोण योग गुणधर्म से)
या 90° + ∠B + ∠B = 180°
[∵ ∠A = 90° (दिया है), तथा ∠B = ∠C समीकरण (i) से)]
2∠B = 180° – 90°
2∠B = 90°
∠B = 45°
∠C = ∠B
∠C = 45°
प्रश्न 8.
दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।
हल:
माना कि एक समबाहु त्रिभुज ABC है
AB = BC = AC यदि
AB = BC है तो
∠C = ∠A ….(i) [क्योंकि ये समान भुजाओं के सम्मुख कोण हैं।]
पुन: यदि AB = AC है तो
∠C = ∠B …..(ii) [क्योंकि ये समान भुजाओं के सम्मुख कोण हैं।]

अब समीकरण (i) व (ii) से
∠A = ∠B = ∠C ….(iii)
अब ∆ABC में ∠A + ∠B + ∠C = 180° …..(iv)
(त्रिभुज के कोण योग गुणधर्म से)
या ∠A + ∠A + ∠A = 180° समीकरण (iii) से
या 3∠A = 180°
∠A = 60°
∵ समीकरण (iii) के अनुसार
∠A = ∠B = ∠C
अर्थात् ∠A = ∠B = ∠C = 60°
अतः यह कहा जा सकता है कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।