Chapter 7 Congruence of Triangles Exercise 7.2
Question 1.
Which congruence criterion do you use in the following?
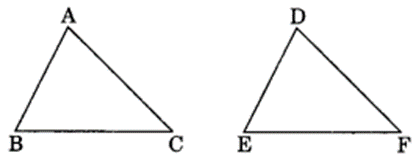
(a) Given:
AC = DF
AB = DE
BC = EF
So, ∆ABC = ∆DEF
(b) Given:
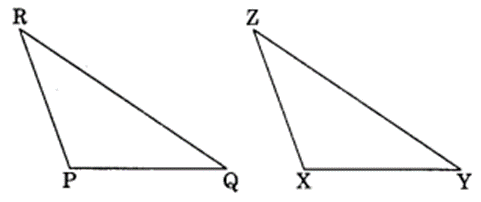
ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ∆PQR ≅ ∆XYZ
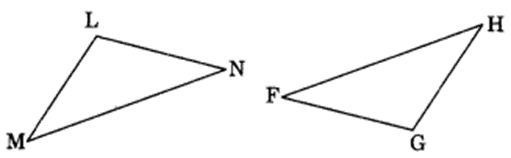
(c) Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ∆LMN = ∆GFH
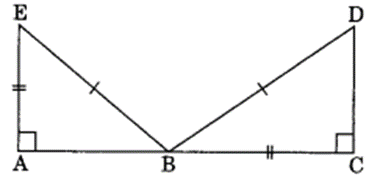
(d) Given:
EB = DB
AE = BC
∠A = ∠C = 90°
∆ABE = ∆CDB
Solution:
(a) ∆ABC ≅ ∆DEF (BY SSS rule)
(b) ∆PQR ≅ ∆XYZ (BY SAS rule)
(c) ∆LMN ≅ ∆GFH (BY ASA rule)
(d) ∆ABE ≅ ∆CDB (BY RHS rule)
Question 2.
You want to show that ∆ART = ∆PEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR =
(ii) RT =
(iii) AT =

(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and
(ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ZA
(ii) ZT
Solution:
(a) For SSS criterion, we need
(i) AR = PE
(ii) RT = EN
(iii) AT = PN
(b) For SAS criterion, we need
(i) RT = EN and
(ii) PN = AT
(c) For ASA criterion, we need
(i) ∠A = ∠P
(ii) ∠T = ∠N
Question 3.
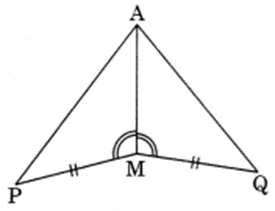
You have to show that ∆AMP ≅ ∆AMQ. In the fallowing proof, supply the missing reasons.
Steps | Reasons |
(i) PM = QM | (i) |
(ii) ∠PMA – ∠QMA | (ii) |
(iii) AM = AM | (iii) |
(iv) ∆AMP = ∆AMQ | (iv) |
Solution:
Steps | Reasons |
(i) PM = QM | (i) Given |
(ii) ∠PMA = ∠QMA | (ii) Given |
(iii) AM = AM | (iii) Common |
(iv) ∆AMP = ∆AMQ | (iv) SAS rule |
Question 4.
In ∆ABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ∆PQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°.
A student says that ∆ABC = ∆PQR by AAA congruence criterion. Is he justified? Why or why not?
Solution:
The student is not justified because there is not criterion for AAA congruence rule.

Example: In ∆ABC and ∆PQR, we have ∠A = 30°, ∠B = 40°, ∠C = 110°
∠P = 30°, ∠Q = 40°, ∠R = 110°
But ∆ABC is not congruent to ∆PQR.
Question 7.
In a squared sheet, draw two triangles of equal areas such that:
(i) the triangles are congruent.
(ii) the triangle are not congruent.
What can you say about their perimeters?
Solution:
(i) On the given square sheet, we have draw two congruent triangles i.e.
∆ABC = ∆DEF
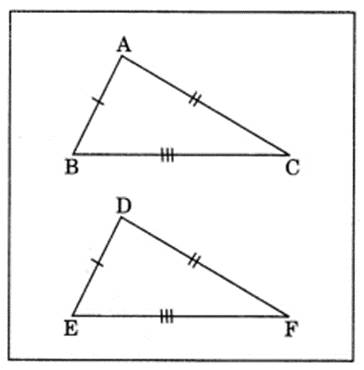
such that
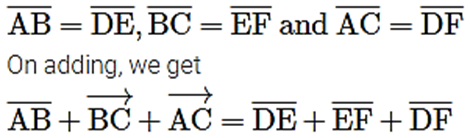
i.e. perimeters of ∆ABC = Perimeter of ∆DEF
(ii) On the other square sheet, we have drawn two triangles ABC and PQR which are not congruent.
Such that
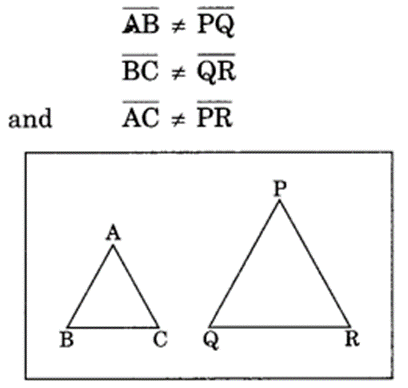
Adding both sides, we get
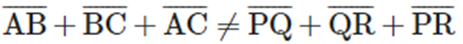
i.e., perimeter of ∆ABC ≠ the perimeter of ∆PQR.
Question 8.
Draw a rough sketch of two triangles, such that they have five pairs of congruent parts but still
the triangles are not congruent.
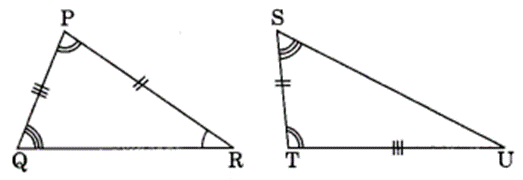
Solution:
We have ∆PQR and ∆TSU
∠Q = ∠S (Given)
∠P = ∠T (Given)
∠R = ∠U (Given)
Since non of the criteria of congruence is relevant here.
∴ ∆PQR and ∆TSU are not congruent.

Question 10.
Explain, why ∆ABC = ∆FED
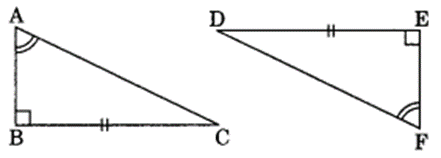
Solution:
In ∆ABC and ∆FED
∠B = ∠E = 90° (Given)
∠A = ∠F (Given)
∴ ∠A + ∠B = ∠E + ∠F
180° – ∠C = 180° – ∠D
[Angle sum property of triangles]
∴ ∠C =∠D
BC = ED (Given)
∴ ∆ABC = ∆FED (By ASA rule)






Question 8.
Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Solution:
In some special cases (which depend on the lengths of the sides and the size of the angle involved),
SSA is enough to show congruence. However, it is not always enough. Consider the following triangles :

Here side AB is congruent to side DE (S) side AC is congruent to side DF(S) angle C is congruent to angle F(A)
But the triangles are not congruent, as we can see.
What happens is this : If we draw a vertical line through point A in the first triangle, we can sort of “flip” side AB around this line to get the second triangle. If we were to lay one triangle on top of the other and draw the vertical line, this how it would look.
Clearly, side DE is just side AB flipped around the line. So, we have not changed the length of the side, and the other side AC (or DF) is unchanged, as is angle C (or F). So, these two triangles that have the same SSA information, but they are not congruent.
