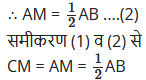Chapter 8 चतुर्भुज Ex 8.2
प्रश्न 1.
ABCD एक चतुर्भुज है जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य- बिन्दु हैं (देखिए आकृति)। AC उसका एक विकर्ण है। दर्शाइए कि
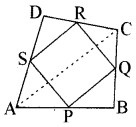

(iii) हमने यह भी सिद्ध किया है कि
PQ ∥ AC तथा SR = AC
अर्थात् PQ ∥ SR
क्योंकि दो रेखाएँ जो दी गई रेखा के समान्तर होती हैं, परस्पर समान्तर होती हैं।
अब PQ = SR तथा PQ ∥ SR
हम जानते हैं कि यदि चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर और समान्तर होता है तो यह एक समान्तर चतुर्भुज होता है।
∴ PQRS एक समान्तर चतुर्भुज है।
प्रश्न 2.
ABCD एक समचतुर्भुज है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं। दर्शाइए कि चतुर्भुज PQRS एक आयत है।
हल:
दिया है-∆BCD एक समचतुर्भुज है जिसकी भुजाओं AB, BC, CD तथा DA के मध्यबिन्दु क्रमशः P, Q, R और S हैं। PQ, QR, RS और SP को मिला दिया।
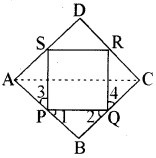
सिद्ध करना है-PQRS एक आयत है।
उपपत्ति – ∆ABC में, AB तथा BC का मध्य बिन्दु P और Q है। अतः मध्य-बिन्दु प्रमेय के अनुसार,
![]()
इसी प्रकार ∆ADC में, CD तथा AD का मध्य-बिन्दु R और S हैं।
अतः मध्य-बिन्दु प्रमेय के अनुसार, SR ∥ AC और SR = AC …..(ii)
अब समीकरण (i) व (ii) से PQ ∥ SR और PQ = SR
अत: PQRS एक समान्तर चतुर्भुज है क्योंकि चतुर्भुज PQRS में सम्मुख भुजाओं PQ और SR एक युग्म समान एवं समान्तर है।
अब ABCD एक समचतुर्भुज है। (दिया है)
अतः AB = BC
![]()
या PB = BQ
या ∠1 = ∠2 क्योंकि त्रिभुज की बराबर भुजाओं के सम्मुख कोण भी बराबर होते हैं।
अब ∆APS और ∆CQR में
AP = CQ

इसी प्रकार AS = CR तथा PS = QR
[क्योंकि ये समान्तर चतुर्भुज PQRS की सम्मुख भुजाएँ हैं।]
∴ ∆APS = ∆CQR (सर्वांगसमता के नियम SSS के अनुसार)
∠3 = ∠4 (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)
अब ∠1 + ∠SPQ + ∠3 = 180° और ∠2 + ∠PQR + ∠4 = 180° [रैखिक युग्म अभिगृहीत से]
∴ ∠1 + ∠SPQ + ∠3 = ∠2 + ∠PQR + ∠R
∴ ∠1 = ∠2 तथा ∠3 = ∠4
∠SPQ = ∠PQR …..(iii)
∵ PQRS एक समान्तर चतुर्भुज है, अतः
∠SPQ + ∠PQR = 180° …..(iv)
क्योंकि SP || RQ तथा PQ तिर्यक रेखा इन्हें काटती है और तिर्यक रेखा के एक ही ओर के अंत:कोणों का योगफल 180° होता है। समीकरण (iii) व (iv) से
SPQ + ∠SPQ = 180°
या 2 ∠SPQ = 180°
या SPQ = 90°
पुनः समीकरण (iii) तथा (iv) से
PQR + ∠PQR = 180°
या 2 ∠PQR = 180°
![]() 0
0
अर्थात् PQRS एक समान्तर चतुर्भुज है
जिसमें ∠SPQ = 90° और PQR = 90° अत: PQRS एक आयत है।
प्रश्न 3.
ABCD एक आयत है, जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
हल:
दिया है-प्रश्नानुसार एक आयत ABCD है जिसमें इसकी भुजाओं AB, BC, CD और DA के मध्य बिन्दु क्रमशः P, Q, R और S हैं। चित्र में PQ, QR, RS और SP को मिलाया गया है।
सिद्ध करना है – PQRS एक समचतुर्भुज है।
रचना – A तथा C को मिलाया।
उपपत्ति – चित्रानुसार ∆ABC में भुजाओं AB तथा BC के मध्य-बिन्दु क्रमशः P और Q हैं।
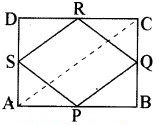
![]()
∆ADC में R और S क्रमशः CD और AD के मध्य-बिन्दु हैं । अतः
SR ∥ AC और SR = FAC …..(ii) अब समीकरण (i) तथा (ii) से
PQ ∥ SR और PQ = SR …..(iii) अर्थात् PQRS एक समान्तर चतुर्भुज है।
∴ ABCD एक आयत है। (दिया है)
या AD = BC
![]()
या AS = BQ …(iv)
∆APS और ∆BPQ में
AP = BP [क्योंकि P बिन्दु AB का मध्य बिन्दु है।]
∠PAS = ∠PBQ = 90°
तथा AS = BQ (iv से)
∴ ∆APS = ∆BPQ
(सर्वांगसमता के नियम SAS के अनुसार)
या PS = PQ (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।)
समीकरण (iii) व (iv) से हम कह सकते हैं कि PQRS एक ऐसा समान्तर चतुर्भुज है जिसमें
PS = PQ अर्थात् दो आसन्न भुजाएँ बराबर हैं।
अतः PQRS एक समचतुर्भुज है।
प्रश्न 4.
ABCD एक समलम्ब है, जिसमें AB ∥ DC है। साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य-बिन्दु है। E से होकर एक रेखा AB के समान्तर खींची गई है, जो BC को F पर प्रतिच्छेद करती है ( देखिए आकृति)। दर्शाइए कि F भुजा BC का मध्य-बिन्दु है।
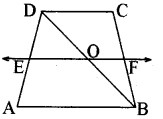
हल:
प्रश्नानुसार माना कि EF रेखा को विकर्ण BD, O बिन्दु पर प्रतिच्छेदित करता है।
अब ∆DAB में E बिन्दु भुजा AB का मध्यबिन्दु है तथा EO ∥ AB है क्योंकि EF ∥ AB (दिया है) और O, EF का एक भाग है। अतः O बिन्दु
∆DAB की दूसरी भुजा BD का मध्य-बिन्दु है।
हम जानते हैं कि त्रिभुज की एक भुजा के मध्यबिन्दु से दूसरी भुजा के समान्तर खींची गई रेखा तीसरी भुजा को मध्य-बिन्दु पर प्रतिच्छेद करती है।
अब ABCD में बिन्दु 0. BD का मध्य बिन्दु है और OF ∥ DC । क्योंकि EF ∥ AB तथा AB ∥ DC (दिया है)
अत: EF ∥ DC और OF EF का ही एक भाग
∴ F, ∆BCD की भुजा BC का भाग है।
(मध्य-बिन्दु प्रमेय के विलोम के अनुसार)
प्रश्न 5.
एक समान्तर चतुर्भुज ABCD में E और F क्रमशः भुजाओं AB और CD के मध्य-बिन्दु हैं ( देखिए आकृति)। दर्शाइए कि रेखाखण्ड AF और EC विकर्ण BD को समत्रिभाजित करते हैं।
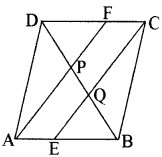
हल:
प्रश्नानुसार दिया गया है कि AB तथा CD भुजाओं के मध्य-बिन्दु क्रमश: E तथा F हैं। अतः

अर्थात् ∆EFC एक समान्तर चतुर्भुज है।
⇒ FA ∥ CE
या FP ∥ CQ
क्योंकि FP, FA का ही एक भाग है और CQ, CE का एक भाग है। …..(ii)
हम जानते हैं कि त्रिभुज की एक भुजा के मध्यबिन्दु से खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
अब ∆DCQ में भुजा CD का मध्य-बिन्दु F है
तथा FF ∥ CQ [समीकरण (ii) से]
अतः भुजा DQ का मध्य-बिन्दु P है।
अर्थात् DP = PQ …..(iii)
इसी प्रकार ∆ABQ में, AB भुजा का मध्यबिन्दु E है
तथा EQ ∥ AP
अत: BP भुजा का मध्यबिन्दु Q है।
अर्थात् BQ = PQ …..(iv)
अब समीकरण (iii) व (iv) से
DP = PQ = BQ …..(v)
अब BD = BQ + PQ + DP
= BQ + BQ + BQ
या BD = 3 BQ
या 3 BQ = BD
![]()
अब समीकरण (v) व (vi) से
DP = PQ = BQ = BD
अर्थात् भुजा BD को बिन्दु P और Q तीन भागों में विभाजित करते हैं। या यह भी कहा जा सकता है कि BD भुजा को AF और CE तीन भागों में विभाजित करते हैं।
प्रश्न 6.
दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिन्दुओं को मिलाने वाले रेखाखण्ड परस्पर समद्विभाजित करते हैं।
हल:
दिया है—एक चतुर्भुज ABCD है जिसमें सम्मुख भुजाओं के मध्य-बिन्दुओं को मिलाने से प्राप्त रेखाखण्ड क्रमश: EG और FH हैं।
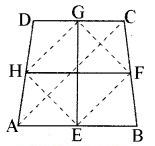
सिद्ध करना है – रेखाखण्ड EG और FH परस्पर समद्विभाजित करते हैं। ..
रचना – बिन्दुओं A व C, E व E F व G, G व _H तथा H व E को मिलाया।
उपपत्ति – ∆ABC में भुजाओं AB तथा BC के मध्य-बिन्दु क्रमश: E व F हैं। अतः
EF ∥ AC
तथा EF = AC ….(i)
इसी प्रकार ∆ADC में भुजाओं CD और AD के मध्य-बिन्दु क्रमशः G व H हैं। अतः
HG ∥ AC तथा HG = FAC …..(ii)
अब समीकरण (i) व (ii) से
EF ∥ HG तथा EF = HG
अत: EFGH एक समान्तर चतुर्भुज है क्योंकि हम जानते हैं कि यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर और समान्तर हो तो वह समान्तर चतुर्भुज होता है। साथ ही समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजक होते हैं। अतः समान्तर चतुर्भुज EFGH के विकर्ण अर्थात् रेखाखण्ड EG और FH परस्पर समद्विभाजित होते हैं।
प्रश्न 7.
ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य-बिन्दु M से होकर BC के समान्तर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि
(i) D भुजा AC का मध्य-बिन्दु है।
(ii) MD ⊥ AC है।
![]()
हल:
(i) AABC में भुजा AB का मध्य-बिन्दु M है, प्रश्नानुसार यह दिया है।

MD ∥ BC
∴ AD = DC
(मध्य-बिन्दु प्रमेय के विलोम के अनुसार) अतः AC भुजा का मध्य बिन्दु D है।
(ii) माना कि भुजा BC के समान्तर खींची गई रेखा m है।
(दिया है) तथा तिर्यक रेखा AC है।
∠1 = ∠C . (संगत कोण)
या ∠1 = 90°
[∵ ∠C = 90°] (दिया है)
अतः MD ⊥ AC.
(iii) आकृति में बने ∆AMD तथा ∆CMD में ∠1 = ∠2 = 90°
(सिद्ध कर चुके हैं) AD = DC (सिद्ध कर चुके हैं)
तथा MD = MD (उभयनिष्ठ भुजा)
अतः ∆AMD ≅ ∆CMD
(सर्वांगसमता के नियम SAS के अनुसार)
∴ AM = CM (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं) …..(1)
दिया है कि AB भुजा का मध्य बिन्दु M है।