Chapter 8 त्रिकोणमिति का परिचय Ex 8.3
प्रश्न 1.
निम्नलिखित का मान निकालिए :
हल-
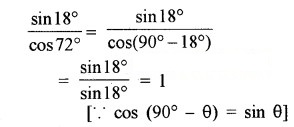
(ii) tan26∘cot64∘tan26∘cot64∘
हल-
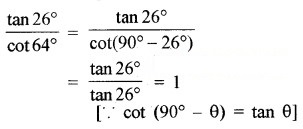
(iii) cos 48° – sin 42°
हल-
cos 48° – sin 42°
= cos (90° – 42°) – sin 42° [∵ cos (90° – θ) = sin θ]
= sin 42° – sin 42°
= 0
(iv) cosec 31° – sec 59°
हल-
cosec 31° – sec 59°
= cosec 31° – sec(90° – 31°)
= cosec 31° – cosec 31° [∵ sec (90° – θ) = cosec θ]
= 0
प्रश्न 2.
दिखाइए कि
(i) tan 48° tan 23° tan 42° tan 67° = 1
हल-
L.H.S. = tan 48° tan 23° tan 42° tan 67°
= tan 48° tan 23° × tan(90° – 48°) × tan(90° – 23°)
= tan 48° × tan 23° × cot 48° × cot 23° [∵ tan (90° – θ) = cot θ]
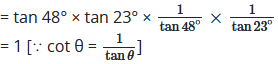
∴ L.H.S. = R.H.S.
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
हल-
L.H.S. = cos 38° cos 52° – sin 38° sin 52°
= cos 38° × cos(90° – 38°) – sin 38° × sin(90° – 38°)
= cos 38° × sin 38° – sin 38° × cos 38° [∵ cos (90° – θ) = sin θ, sin (90° – θ) = cos θ]
= 0
∴ L.H.S. = R.H.S.
प्रश्न 3.
यदि tan 2A = cot (A – 18°), जहाँ 2A एक न्यून कोण है, तो A का मान ज्ञात कीजिए।
हल-
प्रश्नानुसार tan 2A = cot (A – 18°)
A ज्ञात करने के लिए हमें दोनों ओर या तो cot θ चाहिए या tan θ चाहिए। [∵ cot (90° – θ) = tan θ]
⇒ cot(90° – 2A) = cot(A – 18°)
⇒ 90° – 2A = A – 18°
⇒ 3A = 108°
⇒ A = 36°
प्रश्न 4.
यदि tan A = cot B, तो सिद्ध कीजिए कि A + B = 90°
हल-
प्रश्नानुसार tan A = cot B
A + B = 90° दिखाने के लिए
दोनों ओर या तो tan θ चाहिए या cot θ [∵ tan (90° – θ) = cot θ]
⇒ tan A = tan (90° – B)
⇒ A = 90° – B
⇒ A + B = 90°
प्रश्न 5.
यदि sec 4A = cosec (A – 20°), जहाँ 4A एक न्यून कोण है, तो A का मान ज्ञात कीजिए।
हल-
प्रश्नानुसार sec 4A = cosec (A – 20°)
A, ज्ञात करने के लिए हमें दोनों ओर sec θ या cosec θ चाहिए। [∵ cosec (90° – θ) = sec θ]
⇒ cosec (90° – 4A) = cosec (A – 20°)
⇒ 90° – 4A = A – 20°
⇒ 5A = 110°
⇒ A = 22°
प्रश्न 6.

प्रश्न 7.
sin 67° + cos 75° को 0° और 45° के बीच के कोणों के त्रिकोणमितीय अनुपातों के पदों में व्यक्त कीजिए।
हल-
sin 67° + cos 75°
= sin (90° – 23°) + cos (90° – 15°)
= cos 23° + sin 15° [∵ sin(90° – θ) = cos θ और cos(90° – θ) = sin θ]