Chapter 8 Linear Equations in Two Variables Ex 8.2
Question 1.
Which one of the following options is true and why? y = 3x + 5 has
(i) a unique solution
(ii) only two solutions
(iii) infinitely many solutions
Solution:
(iii) A linear equation in two variables has infinitely many solutions.
Question 2.
Write four solutions for each of the following equations
(i) 2x + y = 7
(ii) πx + y = 9
(iii) x = 4y
Solution:
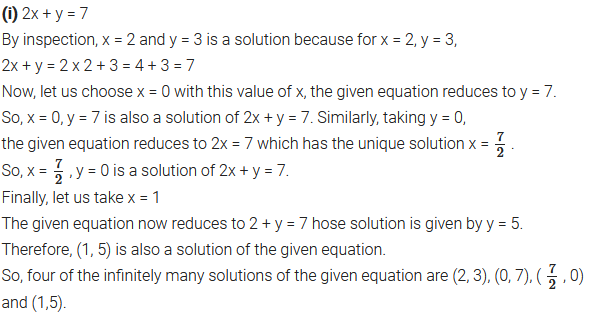

(iii) x = 4y ⇒ x – 4y = 0

Question 3.
Check which of the following are solution of the equation x – 2y = 4 and which are not?
(i) (0, 2)
(ii) (2,0)
(iii) (4,0)
(iv) (√2,4√2)
(v) (1,1)
Solution:
(i) Take x – 2y and put x = 0, y = 2,
we get 0 – 2 x 2 = 0 – 4 = -4 ≠ 4
Hence, (0, 2) is not a solution of x – 2y = 4.
(ii) Take x – 2y and put x = 2, y = 0,
we get 2 – 2 x 0 = 2 – 0 = 2 ≠ 4
Hence, (2, 0) is not a solution of x – 2y = 4.
(iii) Take x – 2y and put x = 4, y = 0;
we get 4 – 2 x 0 = 4 – 0 = 4
Hence, (4, 0) is a solution of x – 2y = 4.
(iv) Take x – 2y and put x = √2, y = 4√2, we get
√2 – 2 x 4√2 = √2 – 8√2 =-7√2 ≠ 4
Hence, (√2,4√2) is not a solution of x – 2y = 4
(v) Take x – 2y and put x = 1, y = 1,
we get 1 – 2 x 1 = 1 – 2 = -1 ≠ 4
Hence, (1,1) is not a solution of x – 2y = 4.
Question 4.
Find the value of k, if x = 2, y = 1 is a solution of the equation 2x + 3 y = k.
Solution:
Take 2x + 3y = k
Put x = 2, y = 1 then we get, 2 x 2 + 3 x 1 = k
⇒ 4 + 3 = k
⇒ k = 7