Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.4
प्रश्न 1.
समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।
हल:
दिया है-एक समान्तर चतुर्भुज ABCD तथा आयत ABEF एक ही आधार तथा एक ही समान्तर रेखाओं के बीच स्थित हैं।
अतः ar (समान्तर चतुर्भुज ABCD) = ar (आयत ABEF)

सिद्ध करना है-AB + BC + CD + AD > AB + BE + EF + AF
उपपत्ति – हम जानते हैं कि चतुर्भुज की सम्मुख भुजाएँ समान होती हैं अतः
AB = CD …..(i)
तथा AB = EF …..(ii)
समीकरण (i) व (ii) से
CD = EF …..(iii)
समीकरण (iii) के दोनों पक्षों में AB जोड़ने पर
AB + CD = AB + EF …..(iv)
हम जानते हैं कि किसी बिन्दु से जो दी हुई रेखा पर स्थित नहीं है, रेखा तक खींचे गए सभी रेखाखण्डों में से लाम्बिक रेखाखण्ड सबसे छोटा होता है।
BE < BC तथा AF < AD
या BC > BE
तथा AD > AF
BC + AD > BE + AF …..(v)
अब समीकरण (iv) व (v) से। AB + BC + CD + AD > AB + BE + EF + AF (इति सिद्धम्)
प्रश्न 2.
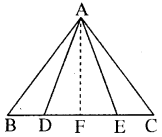
आकृति में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar (ABD) = ar (ADE) = ar (AEC) है।
क्या आप अब उस प्रश्न का उत्तर दे सकते हैं, जो आपने इस अध्याय की ‘भूमिका’ में छोड़ दिया था कि “क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया है”?
हल:
प्रश्नानुसार एवं चित्रानुसार यह देखा जा सकता है कि दिए गए ∆ABC में बिन्दु D और E, भुजा BC को तीन बराबर भागों में इस प्रकार विभाजित करते हैं कि
BD = DE = EC

अब समीकरण (ii), (iii) व (iv) से ar (∆ABD) = ar (∆ADE) = ar (∆AEC)
(इति सिद्धम्) [टिप्पणी-ध्यान दीजिए कि BD = DE = EC लेने से ∆ABC तीन त्रिभुजों ABD, ADE और AEC में विभाजित हो जाता है जिनके क्षेत्रफल बराबर हैं। इसी प्रकार, BC को n बराबर भागों में विभाजित करके और इस भुजा को विभाजित करने वाले बिन्दुओं को सम्मुख शीर्षA से मिलाकर आप इस त्रिभुज को बराबर क्षेत्रफलों वाले n त्रिभुजों में विभाजित कर सकते हैं।]
प्रश्न 3.
आकृति में, ABCD, DCFE और ABFE समान्तर चतुर्भुज हैं। दर्शाइए कि ar (ADE) = ar (BCF) है।

हल:
चूँकि हम जानते हैं कि समान्तर चतुर्भुज की आमने-सामने की भुजाएँ बराबर होती हैं। अतः समान्तर चतुर्भुज ABFE में
AE = BF और AB = EF इसी प्रकार समान्तर चतुर्भुज DCFE में ।
DE = CF और DC = EF तथा समान्तर चतुर्भुज ABCD में
AD = BC और AB = DC अब AADE तथा A BCF में
AE = BF [क्योंकि ये समान्तर चतुर्भुज ABFE की सम्मुख भुजाएँ हैं।]
DE = CF [क्योंकि ये समान्तर चतुर्भुज DCFE की सम्मुख भुजाएँ हैं।]
तथा AD = BC [क्योंकि ये भी समान्तर चतुर्भुज ABCD की सम्मुख भुजाएँ हैं।]
अतः ∆ADE = ∆BCF [सर्वांगसमता के नियम SSS के अनुसार]
अतः ar (∆ADE) = ar (∆BCF)
क्योंकि दो सर्वांगसम आकृतियों का क्षेत्रफल सदैव समान होता है।
प्रश्न 4.
आकृति में, ABCD. A एक समान्तर चतुर्भुज है और BC को एक बिन्दु तक इस प्रकार बढ़ाया गया है कि AD = CQ DA है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है, तो दर्शाइए कि ar (BPC) = ar (DPQ) है।
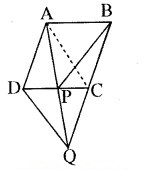
[संकेत : AC को मिलाइए।]
हल:
दिए गए चित्र में बिन्दु A को C से मिलाया। अब चूँकि ∆APC तथा ∆BPC एक ही आधार PC तथा एक ही समान्तर रेखाओं PC तथा AB के बीच स्थित हैं। अतः
ar (∆APC) = ar (∆BPC) …..(i)
चित्रानुसार एवं प्रश्नानुसार ABCD एक समान्तर चतुर्भुज है।
अतः AD = BC (क्योंकि समान्तर चतुर्भुज की सम्मुख भुजाएँ समान होती हैं।)
BC = CQ (दिया है)
AD = CQ
अब AD ∥ CQ (क्योंकि CQ, बढ़ाई गई BC है)
AD = CQ
∴ ADQC एक समान्तर चतुर्भुज है क्योंकि यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर और समान्तर हो, तो वह समान्तर चतुर्भुज होता है।
पुनः क्योंकि समान्तर चतुर्भुज के विकर्ण एकदूसरे को समद्विभाजित करते हैं।
अतः AP = PQ और CP = DP
अब ∆APC तथा ∆DPQ से
AP = PQ (सिद्ध कर चुके हैं)
∠APC = ∠DPQ (शीर्षाभिमुख कोण)
तथा PC = PD(सिद्ध कर चुके हैं)
∴ ∆APC ≅ ∆DPQ ……(ii)
अर्थात् ar (∆APC) = ar (∆DPQ) (क्योंकि सर्वांगसम आकृतियों का क्षेत्रफल सदैव समान होता है।)
अब समीकरण (i) व (ii) से ar (∆BPC) = ar (∆DPQ) (इति सिद्धम्)
प्रश्न 5.
आकृति में, ABC और BDE दो समबाह – त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि


[संकेत : EC और AD को मिलाइए। दर्शाइए कि BE ∥ AC और DE ∥ AB है, इत्यादि।]
हल:
चित्रानुसार EC और AD को मिलाया। चूँकि AABC एक समबाहु त्रिभुज है,
अतः ∠A = ∠B = ∠C = 60°
तथा A BDE भी एक समबाहु त्रिभुज है अतः
∠B = ∠D = ∠E = 60°
यदि हम यह मान लें कि AC तथा BE दो रेखाएँ हैं तथा BC एक तिर्यक रेखा इन्हें काटती है तो
∠B = ∠C = 60° (एकान्तर कोण)
अर्थात् BE ∥ AC
क्योंकि यदि एकान्तर कोण बराबर होते हैं तो रेखाएँ समान्तर होती हैं।
इसी प्रकार यदि AB तथा DE दो रेखाएँ हैं
तथा BF एक तिर्यक रेखा इन्हें काटती है तो
∠B = ∠D = 60° (एकान्तर कोण)

क्योंकि माध्यिका त्रिभुज को बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
BE ∥ AC
अतः ∆BEC और ∆BAE एक ही आधार BE तथा एक ही समान्तर रेखाओं BE तथा AC के बीच स्थित हैं।
∴ ar (∆BEC) = ar (∆BAE) …..(iv)

(iv) ∴ ∠BDE = ∠ABD = 60° (दिया है) परन्तु ये एकान्तर कोणों का युग्म है।
AB ∥ DE
अब ∆BDE और ∆ADE एक ही आधार DE तथा एक ही समान्तर रेखाओं AB और DE के बीच स्थित हैं
अतः ar (∆BDE) = ar (∆ADE)
दोनों पक्षों में से ar (∆FED) घटाने पर ar (∆BDE) – ar (∆FED) = ar (∆ADE) – ar (∆FED)
या ar (∆BFE) = ar (∆AFD)
(v) ∆BDE तथा ∆AED एक ही आधार DE तथा एक ही समान्तर रेखाओं AB तथा ED के बीच स्थित हैं
अतः ar (∆BDE) = ar (∆AED) दोनों पक्षों में से ar (∆FED) को घटाने पर ar (∆BDE) – ar (∆FED) = ar (∆AED) – ar (∆FED)
या ar (∆BFE) = ar (∆AFD) …..(v)
एक समबाहु त्रिभुज में खींची गई माध्यिका भुजा पर लम्ब होती है।
अत: AD ⊥ BC
क्योंकि AD भुजा ∆ABC की माध्यिका है।
अत: ar (∆AFD) = 1/2 × FD × AD …..(vi)
अब BC भुजा पर E बिन्दु से एक लम्ब रेखा EG खींची
अर्थात् EG ⊥ BC
∴ ar (∆FED) = 1/2 × FD × EG …..(vii)
समीकरण (vi) में समीकरण (vii) का भाग देने पर

(क्योंकि भुजा BC का मध्य-बिन्दु D है)
![]()
या ar (∆AED) = 2 ar (∆FED) …..(viii)
अब समीकरण (v) व (viii) से
ar (∆BFE) = 2 ar (∆FED) (इति सिद्धम्) (vi)
ar (∆AFC) = ar (∆AFD) + ar (∆ADC) = 2 ar (∆FED) + 1/2ar (∆ABC) [समीकरण (viii) का प्रयोग करने पर
हम यह भी जानते हैं कि माध्यिका त्रिभुज को बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।
अतः ar (∆AFC) = 2 ar (∆FED) + [4 ar (A BDE)] [भाग (i) के परिणाम से]
= 2 ar (∆FED) + 2 ar (∆BDE) = 2 ar (∆FED) + 2 ar (∆AED)
क्योंकि ∆BDE तथा ∆AED एक ही आधार ED तथा एक ही समान्तर रेखाओं AB तथा DE के बीच स्थित हैं।]
= 2 ar (∆FED) + 2 [ar (∆AFD) + ar (∆FED)]
= 2 ar (∆FED) + 2 ar (∆AFD) + 2 ar (∆FED)
= 4 ar (∆FED) + 2 [2 ar (∆FED)] [समीकरण (viii) से]
= 4 ar (∆ FED) + 4 ar (∆FED)
या ar (∆AFC) = 8 ar (A FED)
या 8 ar (∆FED) = ar (∆AFC)
या ar (∆FED) = 1/8ar (∆AFC) (इति सिद्धम्)
प्रश्न 6.
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते हैं। दर्शाइए कि ar (APB) × ar (CPD) = ar (APD) × ar (BPC) है।
[संकेत : A और C से BD पर लम्ब खींचिए।]
हल:
दिया है-एक चतुर्भुज ABCD है जिसमें विकर्ण क्रमश: AC तथा BD परस्पर P बिन्दु पर प्रतिच्छेदित करते हैं।
सिद्ध करना है-ar (∆APB) × ar (∆CPD) = ar (∆APD) × ar (BPC)
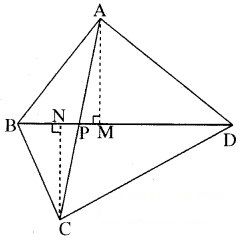
रचना-चित्रानुसार बिन्दु A से AM ⊥ BD
तथा बिन्दु C से CN ⊥ BD खींची। उपपत्ति

समीकरण (ii) में (i) से भाग देने पर

या ar (∆APD) × ar (∆BPC) = ar (∆ABP) × ar (∆CDP) (इति सिद्धम्)
प्रश्न 7.
P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिन्दु हैं तथा R रेखाखण्ड AP का मध्य-बिन्दु है। दर्शाइए कि

(iii) ar (PBQ) = ar (ARC)
हल:
(i) प्रश्नानुसार ∆ABC में बिन्दु P तथा Q क्रमशः भुजाओं AB और BC के मध्य-बिन्दु हैं। AQ तथा FC को मिलाइए। A ABQ की माध्यिका QR है।




अब समीकरण (ix) व (x) के अनुसार
ar (∆PBQ) = ar (∆ARC) (इति सिद्धम्)
प्रश्न 8.
आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखण्ड AX ⊥ DE भुजा BC को बिन्दु Y पर मिलता है। दर्शाइए कि
(i) ∆MBC ≅ ∆ABD
(ii) ar (BYXD) = 2 ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ∆FCB ≅ ∆ACE

(v) ar (CYXE) = 2 ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
हल:
(i) प्रश्नानुसार दिए गए चित्र में ∆MBC और ∆ABD में
BC = BD [वर्ग BCED की भुजाएँ]
∠MBC = ∠ABD (क्योंकि प्रत्येक 90° + ∠ABC)
तथा MB = AB [वर्ग ABMN की भुजाएँ]
अतः ∆MBC ≅ ∆ABD (सर्वांगसमता के नियम SAS के अनुसार) (इति सिद्धम् )
(ii) अब AABD और आयत BYXD एक ही आधार BD और एक ही समान्तर रेखाओं BD और AX _के बीच स्थित हैं। अतः

(iii) अब A MBC और वर्ग ABMN एक ही आधार MB और एक ही समान्तर रेखाओं MB तथा NC के बीच स्थित हैं। अतः .
![]()
समीकरण (i) व (ii) से
ar (BYXD) = ar (ABMN) (इति सिद्धम् )
(iv) अब ∆FCB तथा ∆ACE में
CB = CE [वर्ग BCED की भुजाएँ]
∠FCB = ∠ACE (क्योंकि प्रत्येक कोण 90° + ∠BCA)
तथा FC = AC [वर्ग ACFG की भुजाएँ]
अतः ∆FCB = ∆ACE (सर्वांगसमता के नियम SAS के अनुसार) (इति सिद्धम् )
(v) चित्रानुसार ∆ACE और वर्ग CYXE एक ही आधार CE और एक ही समान्तर रेखाओं CE तथा AX के बीच स्थित हैं अतः

या ar (CYXE) = 2 ar (A FCB) (इति सिद्धम्)
(vi) वर्ग ∆CFG और ∆BCF एक ही आधार CF और एक ही समान्तर रेखाओं CF और BG के बीच स्थित हैं
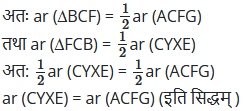
(vii) भाग (iii) और (iv) से
ar (BYXD) = ar (AMBN) और ar (CYXE) = ar (ACFG) जोड़ने पर हमें प्राप्त होता है।
ar (BYXD) + ar (CYXE) = ar (ABMN) + ar (ACFG)
या ar (BCED) = ar (ABMN) + ar (ACFG) (इति सिद्धम् )