Chapter 10 वृत्त Ex 10.4

Chapter 10 वृत्त Ex 10.4

प्रश्न 1.
5 cm तथा 3 cm त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 cm है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।
हल:
माना कि दो वृत्त जिनके केन्द्र O और O’ हैं, परस्पर बिन्दुओं A और B पर प्रतिच्छेद करते हैं। A और B को मिलाने पर, AB उभयनिष्ठ जीवा है।

त्रिज्या OA = 5 cm, त्रिज्या O’A = 3 cm.
उनके केन्द्रों के बीच की दूरी 00′ = 4 cm.
हम देखते हैं कि त्रिभुज AOO’ में;
5² = 4² + 3²
⇒ 25 = 16 +9
⇒ 25 = 25
∆ AO’O में पाइथागोरस का परिणाम संतुष्ट होता
अतः, ∆ AO’O एक समकोण त्रिभुज है जिसमें O’ पर समकोण है।
जैसा कि हम जानते हैं कि वृत्त के केन्द्र से जीवा पर गिराया गया लम्ब जीवा को समद्विभाजित करता है।
अतः O’ जीवा AB का मध्य-बिन्दु है। साथ ही O’ दूसरे वृत्त का केन्द्र है।
इसलिए जीवा AB की लम्बाई = दूसरे वृत्त का व्यास
∴ जीवा AB की लम्बाई = 2 × 3 cm = 6 cm

वैकल्पिक:
माना कि दो वृत्त, जिनके केन्द्र O और O’ हैं, परस्पर बिन्दुओं A और B पर प्रतिच्छेद करते हैं। माना कि उभयनिष्ठ जीवा AB, 00′ को C पर प्रतिच्छेद करती है।

अतः OC = x cm
∴ OC = 4 – x cm
हम जानते हैं कि दो वृत्तों के केन्द्रों को मिलाने वाली रेखा वृत्तों को उभयनिष्ठ जीवा का लम्ब समद्विभाजक होते हैं।
∴ समकोण ∆ OCA में, पाइथागोरस प्रमेय के अनुसार
AC² + OC² = OA²
⇒ AC² + x² = 5²
⇒ AC² = 25 – x² …..(i)
इसी प्रकार ∆ACO’ में,
AC² + O’C² = AO²
⇒ AC² + (4 – x)² = 3²
⇒ AC² = 9 – (4 – x)²….(ii)
समीकरण (i) और (ii) से
25 – x² = 9 – (4 – x)²
⇒ 25 – x² = 9 – (16 + x² – 8x)
⇒ 25 – x² = 9 – 16 – x² + 8x
⇒ – 8x = 9 – 16 – 25 – x² + x²
⇒ – 8x = – 32
⇒ x = 4
∴ CO’ = 4 – x
⇒ CO’ = 4 – 4
⇒ CO’ = 0
इसका अर्थ है कि O’, C के साथ संपाती हैं।
∴ AC = त्रिज्या AO’ = 3 cm
जीवा AB की लम्बाई = केन्द्र O’ वाले वृत्त का व्यास
जीवा AB की लम्बाई = 2 × AO’
= 2 × AC = 2 × 3 = 6 cm.

प्रश्न 2.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं।
हल:
माना कि एक वृत्त जिसका केन्द्र 0 है, की दो समान जीवाएँ AB तथा CD वृत्त के अन्दर E पर प्रतिच्छेद करती हैं। हमें सिद्ध करना है कि
(a) AE = CE
(b) BE = DE.

रचना: OM ⊥ AB, ON ⊥ CD खींचिए, OE को मिलाइए।
उपपत्ति – समकोण ∆ OME और समकोण ∆ ONE में
∠OME =∠ONE (प्रत्येक 90°)
OM = ON
[∵ समान जीवाएँ वृत्त के केन्द्र से समदूरस्थ होंगी]
कर्ण OE = कर्ण OE (उभयनिष्ठ भुजाएँ)
∴ ∆OME ≅ ∆ ONE
(सर्वांगसमता के नियम R.H.S. के अनुसार)
∴ ME = NE …….(i)
(क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग) अब, O वृत्त का केन्द्र है और
OM ⊥ AB
∴ AM = 1/2AB …..(ii)
[क्योंकि वृत्त के केन्द्र से जीवा पर लम्ब जीव को समद्विभाजित करता है]
इसी प्रकार, NC = 1/2CD …….. (iii)
परन्तु AB = CD (दिया है)
समीकरण (ii) और (iii) से
AM = NC …..(iv)
साथ ही, MB = DN …..(v)
समीकरण (i) और (iv) को जोड़ने पर
AM + ME = NC + NE
⇒ AE = CE भाग (a) सिद्ध हुआ |
अब AB = CD (दिया है)
AE = CE(ऊपर सिद्ध किया है)
AB – AE = CD – CE
BE = DE भाग (b) सिद्ध हुआ

प्रश्न 3.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अंदर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
हल:
माना कि एक वृत्त जिसका केन्द्र O है, की दो समान जीवाएँ AB तथा CD वृत्त के अन्दर E पर प्रतिच्छेद करती हैं। हमें सिद्ध करना है कि
∠OEM = ∠OEN.

रचना: OM ⊥ AB, ON ⊥ CD खींचिए। OE को मिलाइए।
उपपत्ति- समकोण त्रिभुजों OME और ONE में
∠OME = ∠ONE (प्रत्येक 90°)
OM = ON
क्योंकि वृत्त की समान जीवाएँ केन्द्र से समदूरस्थ होती हैं।
कर्ण OE = कर्ण OE (उभयनिष्ठ)
∴ ∆ OME ≅ ∆ ONE
(सर्वांगसमता के नियम RHS के अनुसार)
∴ ∠OEM = ∠OEN
(क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग)

प्रश्न 4.
यदि एक रेखा दो संकेन्द्री वृत्तों (एक ही केन्द्र वाले वृत्त) को जिनका केन्द्र O है, A, B, C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB = CD है ( देखिए आकृति)।

हल:
माना वह रेखा l है जो कि दो संकेन्द्रीय वृत्तों को, जिनका केन्द्र 0 है, A, B, C और D पर प्रतिच्छेद करती है।

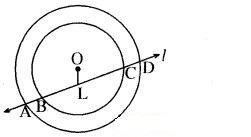
हमें सिद्ध करना है कि
AB = CD
रचना- OL ⊥ l खींचिए।
उपपत्ति- AD बाह्य वृत्त की जीवा है और OL ⊥ AD
∴ AL = LD ….(i)
[∵ केन्द्र से खींचा गया लम्ब, जीवा को समद्विभाजित करता है।]
अब; BC अंत:वृत्त की जीवा है और OL ⊥ BC.
∴ BL = LC …..(ii)
[∵ केन्द्र से खींचा गया लम्ब, जीवा को समद्विभाजित करता है।]
(ii) को (i), में से घटाने पर हमें प्राप्त होता है।
AL – BL = LD – LC
⇒ AB = CD (इति सिद्धम्)

प्रश्न 5.
एक पार्क में बने 5 मीटर त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 मीटर हो, तो रेशमा और मनदीप के बीच की दूरी क्या है ?
हल:
माना कि रेशमा, सलमा और मनदीप की स्थिति को बिन्दुओं A, B और C से दिखाया गया है।
दिया गया है कि रेशमा और सलमा के बीच की दूरी 6 मीटर है तथा सलमा और मनदीप के बीच की दूरी भी 6 मीटर है। इसका अर्थ है कि
AB = BC = 6 मीटर
∴ वृत्त का केन्द्र ∠ABC के समद्विभाजक पर स्थित है।
माना कि M, AC और OB का प्रतिच्छेद बिन्दु है।
पुनः क्योंकि AB = BC
और BM, ∠ABC को समद्विभाजित करता है।
∴ BM ⊥ AC और M, AC का मध्य बिन्दु है।
माना कि OM = x
तब MB = 5 – x
अब, समकोण ∆ OMA से
⇒ OA² = OM² + AM²
5² = x² + AM² …….(i)

पुनः समकोण ∆ AMB से,
AB² = AM² + MB²
⇒ 6² = AM² + (5 – x)² …..(ii)
(i) और (ii) से AMP के मूल्य को बराबर करने हमें प्राप्त होता है
5² – x² = 6² – (5 – x)²
⇒ (5 – x)² – x² = 6² – 5²
⇒ (25 – 10x + x²) – x² = 36 – 25
⇒ 25 – 10x + x² – x = 11
⇒ – 10x = 11 – 25
⇒ – 10x = – 14
⇒ x = 14/10
अतः (i) से, AM² = 5² – x²

∴ AC = 2 MB
= 2 × 4.8 = 9.6 मीटर
अतः रेशमा और मनदीप के बीच की दूरी 9.6 मीटर है।

प्रश्न 6.
20m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कॉलोनी में स्थित है। तीन लड़के अंकुर, सैयद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
हल:
माना कि तीनों लड़कों अंकुर, सैयद तथा डेविड की स्थिति को बिन्दुओं A, B और C से दिखाया गया है। तीनों बिन्दु समान दूरी पर हैं।
∴ AB = BC = AC = a मीटर (माना)

∵ समबाहु त्रिभुज की समान भुजाएँ वृत्त की समान जीवाएँ हैं और वृत्त की समान जीवाएँ केन्द्र से समदूरस्थ होती हैं।
∴ OD = OE = OF = x मीटर (माना)
OA, OB और OC को मिलाइए।
अब, हमारे पास तीन सर्वांगसम त्रिभुजें हैं।
∆ OAB, ∆ OBC और ∆ AOC
∴ ar (∆ AOB) = ar (∆ BOC) = ar (∆ AOC) …..(i)
अब, a भुजा वाली समबाहु ∆ ABC का क्षेत्रफल
= ar (∆ AOB) + ar (∆ BOC) + ar (∆ AOC) ……(ii)
⇒ ar (∆ ABC) = 3 ar (∆ BOC)
[समीकरण (i) व (ii) के अनुसार]

⇒ a = 2√3 x …..(iii)
OE ⊥ BC

[समीकरण (iii) के अनुसार]
⇒ BE = EC = √3 x
अब, समकोण ∆ BEO में,
OE² + BE² = OB²
(पाइथागोरस प्रमेय के अनुसार)
⇒ x + (√3x)² = 20²
⇒ x² + 3x² = 400
⇒ 4x² = 400
⇒ x² = \frac{400}{4}
⇒ x² = 100
⇒ x = √100
⇒ x = 10 m …..(iv)
समीकरण (iii) के आधार पर
a = 2√3x
⇒ a = 2√3 × 10 मीटर
[(iv) का प्रयोग करने पर]
a = 20√3 मी.
अत: किन्हीं दो लड़कों के बीच की दूरी 20√3 मीटर है।