Chapter 10 Circles Ex 10.2
Question 1.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(a) 7 cm Sol.
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution:

Question 2.
In figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°
Solution:
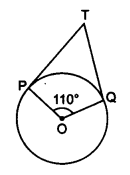
∠OPT = 90°
∠OQT = 90°
∠POQ = 110°
TPOQ is a quadrilateral,
∴ ∠PTQ + ∠POQ = 180° ⇒ ∠PTQ + 110° = 180°
⇒∠PTQ = 180°- 110° = 70°
Hence, correct option is (b).
Question 3.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution:
In AOAP and AOBP
OA = OB [Radii]
PA = PB
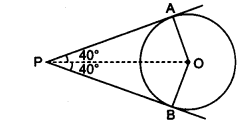

Question 4.
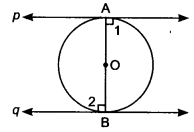
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:
AB is a diameter of the circle, p and q are two tangents.
OA ⊥ p and OB ⊥ q
∠1 = ∠2 = 90°
⇒ p || q ∠1 and ∠2 are alternate angles]
Question 5.
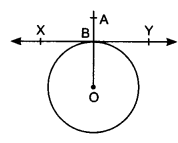
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:
XY tangent to the circle C(0, r) at B and AB ⊥ XY. Join OB.
∠ABY = 90° [Given]
∠OBY = 90°
[Radius through point of contact is perpendicular to the tangent]
∴ ∠ABY + ∠OBY = 180° ⇒ ABOiscollinear
∴ AB passes through centre of the circle.
Question 6.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution:
OA = 5 cm, AP = 4 cm OP = Radius of the circle
∠OPA = 90° [Radius and tangent are perpendicular]

Question 7.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
Radius of larger circle = 5 cm Radius of smaller circle = 3 cm
OP ⊥ AB
[Radius of circle is perpendicular to the tangent]
AB is a chord of the larger circle

Question 8.
A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that AB + CD = AD + BC.
Solution:
AP = AS … (i)
[Lengths of tangents from an external point are equal]
BP = BQ … (ii)
CR = CQ … (iii)
DR = DS … (iv)
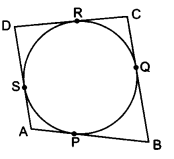
Adding equations (i), (ii), (iii) and (iv), we get
AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
Hence proved.
Question 9.
In figure, XY and X’Y’ are two parallel tangents to a circle , x with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.
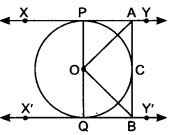
Solution:
Given: Two parallel tangents to a circle with centre O. Tangent AB with point of contact C intersects XY at A and X’Y’ at B To Prove: ∠AOB = 90° with point of contact C intersects XY at A and X’Y’ at B

To Prove: ∠AOB = 90°
Construction: Join OA, OB and OC
Proof: In ∆AOP and ∆AOC

Question 10.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution:
PA and PB are two tangents, A and B are the points of contact of the tangents.

Question 11.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:
Parallelogram ABCD circumscribing a circle with centre O.
OP ⊥ AB and OS ⊥ AD

Question 12.
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.

Solution:
BD = 8 cm and DC = 6 cm
BE = BD = 8 cm
CD = CF = 6 cm
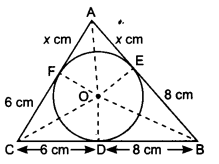
Let AE = AF = x cm
In ∆ABC, a = 6 + 8 = 14 cm
b = (x + 6) cm
c = (x + 8) cm
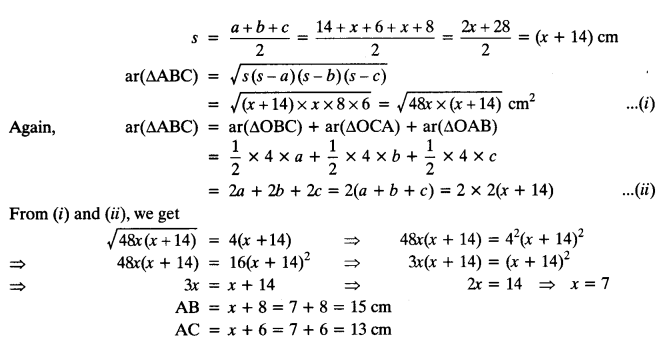
Question 13.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution:
AB touches at P.
BC, CD and DA touch the circle at Q, R and S.
Construction: Join OA, OB, OC, OD and OP, OQ, OR, OS.
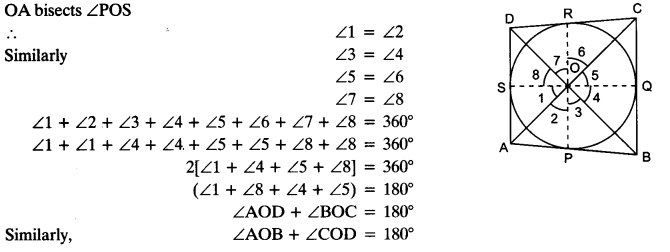
Hence, opposite sides of quadrilateral circumscribing a circle subtend supplementary angles at the centre of a circle.