Chapter 11 परिमाप और क्षेत्रफल Ex 11.4
प्रश्न 1.
एक बगीचा 90 m लम्बा और 75 m चौड़ा है। इसके बाहर चारों तरफ 5 m चौड़ा पथ बनाना है। पथ का क्षेत्रफल ज्ञात कीजिए। बगीचे का क्षेत्रफल हेक्टेअर में भी ज्ञात कीजिए।
हल:
बगीचे की लम्बाई (l) = 90 m, चौड़ाई (b) = 75 m
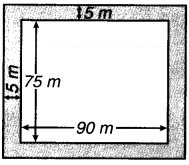
बगीचे का क्षेत्रफल = l × b
= 90 m × 75 m = 6750 m2
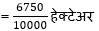
= 0.6750 हेक्टेअर
∵ बगीचे के चारों ओर का पथ आयत बनाता है।
∴ बाह्य आयत की लम्बाई = 90 + 5 + 5 = 100 m
व चौड़ाई = 75 + 5 + 5 = 85 m
∴ पथ सहित बगीचे का बाह्य आयत का क्षेत्रफल
= 100 × 85 = 8,500 m2
अतः पथ का क्षेत्रफल = बाह्य आयत का क्षेत्रफल – बगीचे का क्षेत्रफल
= 8500 m2 – 6750 m2 = 1750 m2
प्रश्न 2.
125 m लम्बाई और 65m चौड़ाई वाले एक आयताकार पार्क के चारों ओर बाहर एक 3 m चौड़ा पथ बना हुआ है। पथ का क्षेत्रफल ज्ञात कीजिए।
हल:
चित्र 11.29 में,
PQ = AB + 2 × पथ की चौड़ाई
= 125 + 2 × 3 = 125 + 6 = 131 m
व QR = BC + 2 × पथ की चौड़ाई
= 65 + 2 × 3 = 65 + 6 = 71 m
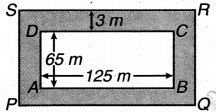
अब, पथ का क्षेत्रफल
= बाह्य आयत PORS का क्षेत्रफल – पार्क ABCD का क्षेत्रफल
= PQ × QR – AB × BC
= 131 × 71 – 125 × 65
= 9301 – 8125 = 1176m2
प्रश्न 3.
8 cm लम्बे और 5 cm चौड़े एक गत्ते पर एक चित्र की पेंटिंग इस प्रकार बनाई गई है कि इसकी प्रत्येक भुजाओं के अनुदिश 1.5 cm चौड़ा हाशिया (margin) छोड़ा गया है। हाशिये का कुल क्षेत्रफल ज्ञात कीजिए।
हल:
चित्र 11.30 में,
PQ = 8 cm, QR = 5 cm
AB = PQ – 2 × हाशिये की चौड़ाई
= 8 – 2 × 1.5 = 8 – 3 = 5 cm
BC = QR – 2 × हाशिये की चौड़ाई
= 5 – 2 × 1.5 = 5 – 3 = 2 cm
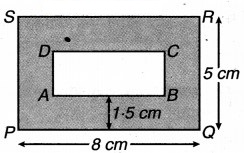
अब, हाशिये का कुल क्षेत्रफल
= गत्ते का क्षेत्रफल – पेंटिंग का क्षेत्रफल
= PQ × QR – AB × BC = 8 × 5 – 5 × 2 = 40 – 10 = 30 cm2
प्रश्न 4.
5.5m लम्बे और 4 m चौड़े कमरे के चारों ओर बाहर 2-25 m चौड़ा एक बरामदा बनाया गया है। ज्ञात कीजिए:
(i) बरामदे का क्षेत्रफल
(ii) ₹ 200 प्रति m2 की दर से बरामदे के फर्श पर सीमेंट कराने का व्यय।
हल:
चित्र 11.31 में,
ABCD कमरा है तथा इसके चारों ओर 2.25 m चौड़ा बरामदा है।
PQ = AB + 2 × बरामदे की चौड़ाई
= 5.5 + 2 × 2.25 = 5.5 + 4.5 = 10 m
QR = BC + 2 × बरामदे की चौड़ाई
= 4 + 2 × 2.25
= 4 + 4.5 = 8.5 m
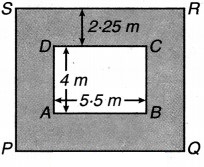
(i) बरामदे का क्षेत्रफल = बाह्य आयतकार भाग PQRS का क्षेत्रफल – कमरे का क्षेत्रफल
= PQ × QR – AB × CD
= 10 × 8.5 – 5.5 × 4
= 85 – 22 = 63 m2
(ii) ₹ 200 प्रति m2 की दर से बरामदे के फर्श पर सीमेंट कराने का कुल व्यय = ₹200 × 63 = ₹ 12,600
प्रश्न 5.
30 m भुजा वाले एक वर्गाकार बगीचे की परिसीमा से लगा भीतर की ओर 1 m चौड़ा पथ बना हुआ है। ज्ञात कीजिए:
(i) पथ का क्षेत्रफल
(ii) ₹ 40 प्रति m2 की दर से शेष भाग पर घास लगवाने का व्यय।
हल:
(i) चित्र 11.32 में,
PQRS बगीचा है। इसके भीतर की ओर 1 m चौड़ा पथ है।
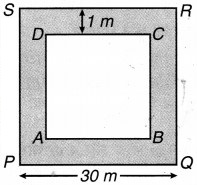
AB = PQ – 2 × पथ की चौड़ाई
= 30 – 2 × 1
= 30 – 2 = 28 m.
BC = OR – 2 × पथ की चौड़ाई
= 30 – 2 × 1
= 30 – 2 = 28m
अब, पथ का क्षेत्रफल = बाह्य वर्ग PQRS का क्षेत्रफल
– अन्त:वर्ग ABCD का क्षेत्रफल
= 30 × 30 – 28 × 28
= 900 – 784
= 116 m2
(ii) बगीचे के शेष भाग का क्षेत्रफल
= ABCD का क्षेत्रफल
= (28 × 28) m2
= 784 m2
∴ ₹ 40 प्रति m2 की दर से बगीचे के शेष भाग पर घास लगवाने का व्यय
= ₹40 × 784
= ₹ 31,360
प्रश्न 6.
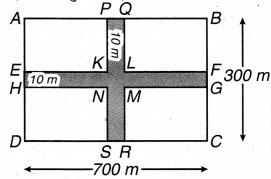
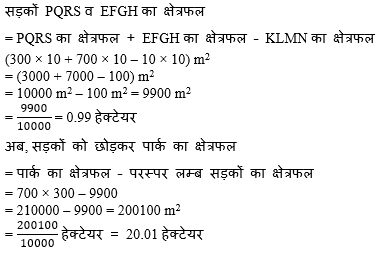
700 m लम्बे और 300 m चौड़े एक आयताकार पार्क के मध्य से होकर जाते 10 m चौड़े दो पथ बने हुए हैं, जो एक-दूसरे पर परस्पर लम्ब और चौपड़ के आकार के हैं। इनमें से प्रत्येक पथ का क्षेत्रफल ज्ञात कीजिए तथा पार्क की भुजाओं को छोड़कर पार्क के शेष भाग का भी क्षेत्रफल ज्ञात कीजिए। उत्तर को हेक्टेयर में दीजिए।
हल:
PQ = EH = KL = KN = 10 m
लम्बाई के अनुदिश सड़क की लम्बाई = 700 m
चौड़ाई के अनुदिश सड़क की लम्बाई = 300 m
प्रश्न 7.
90 m लम्बाई और 60 m चौड़ाई वाले एक आयताकार मैदान में दो पथ बनाए गए हैं, जो भुजाओं के समान्तर हैं, एक-दूसरे को लम्बवत् काटते हैं और मैदान के मध्य से होकर निकलते हैं। यदि प्रत्येक पथ की चौड़ाई 3m हो, तो ज्ञात कीजिए:
(i) पथों द्वारा आच्छादित क्षेत्रफल
(ii) ₹110 प्रति m2 की दर से पथ बनाने का व्यय।
हल:
(i) पथ PQRS का क्षेत्रफल = लम्बाई × चौड़ाई
= 90 × 3 = 270 m2
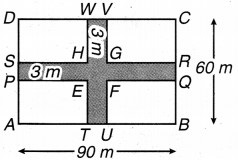
पथ TUVW का क्षेत्रफल = लम्बाई × चौड़ाई
= 60 × 3 = 180 m2
उभयनिष्ठ भाग EFGH का क्षेत्रफल
= 3 × 3 = 9 m2
अत: पथों का कुल क्षेत्रफल = पथ PQRS का क्षेत्रफल + पथ TUVW का क्षेत्रफल – उभयनिष्ठ भाग EFGH का क्षेत्रफल
= 270 m2 + 180 m2 – 9m2
= 450 m2 – 9 m2
= 441 m2
(ii) ₹ 110 प्रति m2 की दर से पथ बनाने का व्यय
= ₹ 110 × 441
= ₹ 48,510
प्रश्न 8.
प्रज्ञा 4 cm त्रिज्या वाले एक वृत्ताकार पाइप के चारों ओर एक रस्सी लपेटती है (जैसा दिखाया गया है) और रस्सी की आवश्यक लम्बाई को काट लेती है। इसके बाद वह उसे 4 cm भुजा वाले एक वर्गाकार बॉक्स के चारों ओर लपेटती है(दिखाया गया है)। क्या उसके पास कुछ और रस्सी बचेगी ? (π = 3.14)
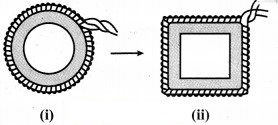
हल:
वृत्ताकार पाइप की त्रिज्या (r) = 4 cm
∴ पाइप की परिधि = 2πr
= 2 × 3.14 × 4 = 25.12 cm
∴ पाइप पर लपेटी गई रस्सी की लम्बाई
= 25.12 cm
अब, वर्ग का परिमाप = 4 × a
= 4 × 4 cm = 16 cm
∴ वर्ग पर लपेटी गई रस्सी की लम्बाई = 16 m
∵ 25.12 cm – 16 cm
∴ 25.12 cm – 16 cm = 9.12 cm.
हाँ, उसके पास 9-12 cm रस्सी और बचेगी।
प्रश्न 9.
संलग्न आकृति एक आयताकार पार्क के मध्य में एक वृत्ताकार फूलों की क्यारी को दर्शाती है। ज्ञात कीजिए:
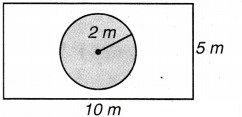
(i) पूरे पार्क का क्षेत्रफल
(ii) फूलों की क्यारी का क्षेत्रफल
(iii) फूलों की क्यारी को छोड़कर, पार्क के शेष भाग का क्षेत्रफल
(iv) क्यारी की परिधि।
हल:
(i) यहाँ, पार्क की लम्बाई (l) = 10m, चौड़ाई = 5 m.
∴ पार्क का क्षेत्रफल = l × b
= 10 × 5 = 50 m2
(ii) फूलों की क्यारी की त्रिज्या (r) = 2 m
∴ फूलों की क्यारी का क्षेत्रफल = 2
= 3.14 × 2 × 2
= 12.56 m2
(iii) फूलों की क्यारी को छोड़कर शेष भाग का क्षेत्रफल
= पार्क का क्षेत्रफल – क्यारी का क्षेत्रफल
= 50 m2 – 12.56 m2
= 37.44 m2
(iv) क्यारी की परिधि = 2πr
= 2 × 3.14 × 2
= 12.56 m
प्रश्न 10.
दी गई आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
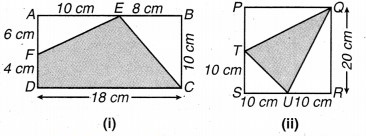
हल:


प्रश्न 11.
चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए। यहाँ, AC = 22 cm, BM = 3 cm, DN = 3 cm, और BM ⊥ AC, DN ⊥ AC.
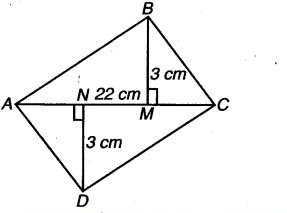
हल:
