Chapter 11 Constructions Ex 11.2
In each of the following, give the justification of the construction also:
Question 1.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:
Steps of Construction:
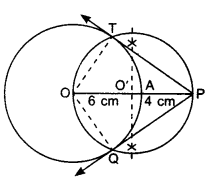
1. Draw a circle of radius 6 cm.
2. Mark a point P at a distance 10 cm from the centre O.
3. Here OP = 10 cm, draw perpendicular bisector of OP, which intersects OP at O’.
4. Take O’ as centre, draw a circle of radius O’O, which passes through O and P and intersects the previous circle at points T and Q.
5. Join PT and PQ, measure them, these are the required tangents.
Justification:
Join OT and OQ.
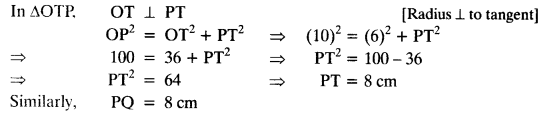
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ PT = PQ.
Question 2.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution:
Steps of Construction:
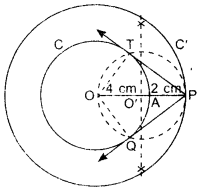
1. Draw concentric circles of radius OA = 4 cm and OP = 6 cm having same centre O.
2. Mark these circles as C and C’.
3. Points O, A and P lie on the same line.
4. Draw perpendicular bisector of OP, which intersects OP at O’.
5. Take O’ as centre, draw a circle of radius OO’ which intersects the circle C at points T and Q.
6. Join PT and PQ, these are the required tangents.
7. Length of these tangents are approx. 4.5 cm.
Justification:
Join OT and OQ.
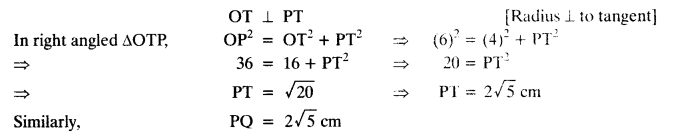
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ PT = PQ.
Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution:
Steps of Construction: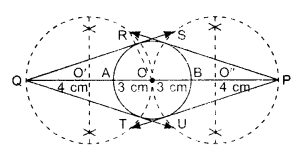
1. Draw a circle of radius 3 cm, having centre O. Mark this circle as C.
2. Mark points P and Q along its extended diameter such that OP = 7 cm and OQ = 7 cm.
3. Draw perpendicular bisector of OQ, intersecting OQ at O’.
4. Draw perpendicular bisector of OP intersecting OP at O”.
5. Take O’ as centre and draw a circle of radius OO’ which passes through points O and Q, intersecting circle C at points R and T.
6. Take O” as centre and draw a circle of radius O”P which passes through points O and P, intersecting the, circle C at points S and U.
7. Join QR and QT; PS and PU, these are the required tangents.

Question 4.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution:
Steps of Construction:
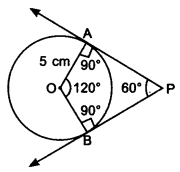
1. Draw a circle of radius 5 cm.
2. As tangents are inclined to each other at an angle of 60°.
∴ Angle between the radii of circle is 120°. (Use quadrilateral property)
3. Draw radii OA and OB inclined to each other at an angle 120°.
4. At points A and B, draw 90° angles. The arms of these angles intersect at point P.
5. PA and PB are the required tangents.
Justification:
In quadrilateral AOBP,
AP and BP are the tangents to the circle.
Join OP.
In right angled AOAP, OA ⊥ PA [Radius is ⊥ to tangent]
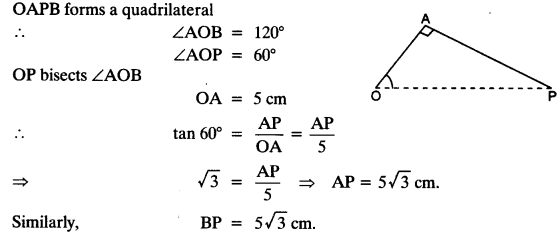
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ PA = PB
Question 5.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution:
Steps of Construction:
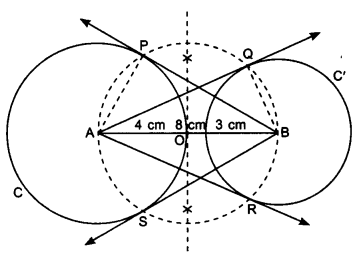
1. Draw a line segment AB = 8 cm.
2. Taking A as centre draw a circle C of radius 4 cm and taking B as centre draw a circle C’ of radius 3 cm.
3. Draw perpendicular bisector of AB, which intersects AB at point O.
4. Taking point O as centre draw a circle of radius 4 cm passing through points A and B which intersect circle C at P and S and circle C’ at points R and Q.
5. Join AQ, AR, BP and BS. These are the required tangents.
Justification:
Join AP.

A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ AQ = AR and BP = BS.
Question 6.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ZB = 90°. BD is the perpendicular Burn B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:
Steps of Construction:
1. Draw a right triangle ABC with AB = 6 cm, BC = 8 cm and ZB = 90°.
2. From B, draw BD perpendicular to AC.
3. Draw perpendicular bisector of BC which intersect BC at point O’.
4. Take O’ as centre and O’B as radius, draw a circle C’ passes through points B, C and D.
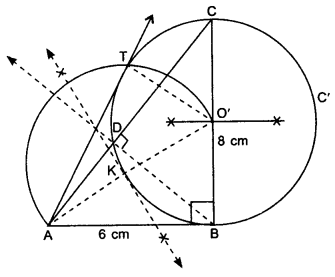
5. Join O’A and draw perpendicular bisector of O’A which intersect O’A at point K.
6. Take K as centre, draw an arc of radius KO’ intersect the previous circle C’ at T.
7. Join AT, AT is required tangent.
Justification:
∠BDC = 90°
∴ BC acts as diameter.
AB is tangent to circle having centre O’
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ AB = AT.
Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution:
Steps of Construction:
1. Draw a circle C’ with the help of a bangle, for finding the centre, take three non-collinear points A, B and C, lying on the circle. Join AB and BC and draw perpendicular bisector of AB and BC, both intersect at a point O,
‘O’ is centre of the circle.
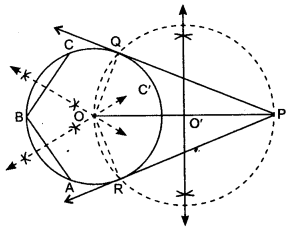
2. Take a point P outside the circle. Join OP.
3. Draw perpendicular bisector of OP, which intersects OP at point O’.
4. Take O’ as the centre with OO’ as radius draw a circle which passes through O and P, intersecting previous circle C’ at points R and Q.
5. Join PQ and PR.
6. PQ and PR are the required pair of tangents.
Justification:
Join OQ and OR.
In AOQP and AOPR, OQ = OR [Radii of the circle]
OP = OP [Common]
∠Q = ∠R = 90° [Radius is ⊥ to tangent]
∆OQP ≅ ∆ORP [by RHS]
∴ PQ = PR [By C.P.C.T]
A pair of tangents can be drawn to a circle from an external point lying outside the circle. These two tangents are equal in lengths.
∴ PQ = PR