Chapter 11 Mensuration Exercise 11.3
Question 1.
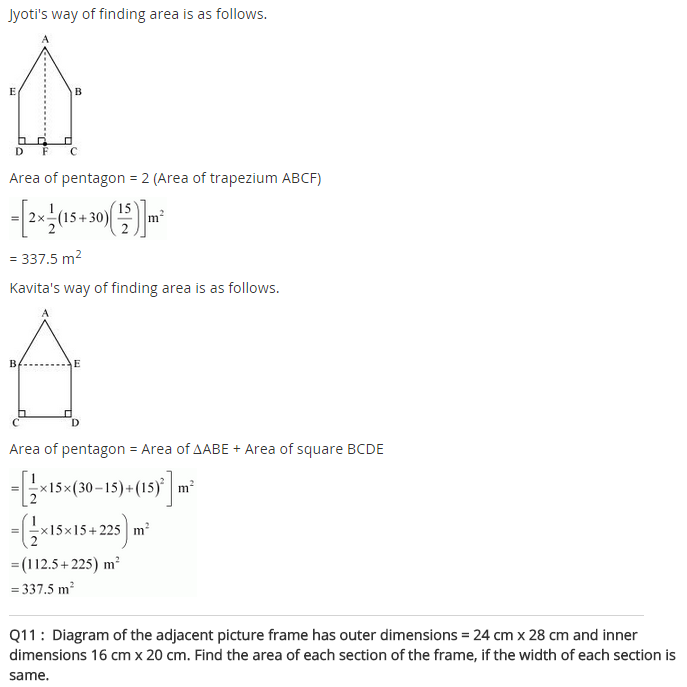
There are two cuboidal boxes as shown in the figure. Which box requires the lesser amount of material to make?
Solution:
(a) Volume of the cuboid = l × b × h = 60 × 40 × 50 = 120000 cm3
(b) Volume of cube = (Side)3 = (50)3 = 50 × 50 × 50 = 125000 cm3
Cuboidal box (a) requires lesser amount of material.
Question 2.
A suitcase with measures 80 cm × 48 cm × 24 cm is to be covered with a tarpaulin cloth. How many metres of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Solution:
Measurement of the suitcase = 80 cm × 48 cm × 24 cm
l = 80 cm, b = 48 cm and h = 24 cm
Total surface area of the suitcase = 2[lb + bh + hl]
= 2 [80 × 48 + 48 × 24 + 24 × 80]
= 2 [3840 + 1152 + 1920]
= 2 × 6912
= 13824 cm2
Area of tarpaulin = length × breadth = l × 96 = 96l cm2
Area of tarpaulin = Area of 100 suitcase
96l = 100 × 13824
l = 100 × 144 = 14400 cm = 144 m
Hence, the required length of the cloth = 144 m.
Question 3.
Find the side of a cube whose surface area is 600 cm2?
Solution:
Total surface area of a cube = 6l2
6l2 = 600
l2 = 100
l = √100 = 10 cm
Hence, the required length of side = 10 cm.
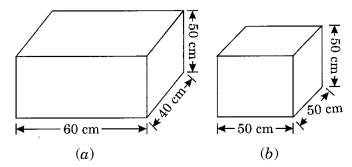
Question 4.
Rukhsar painted the outside of the cabinet of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet?
Solution:
l = 2 m, b = 1.5 m, h = 1 m
Area of the surface to be painted = Total surface area of box – Area of base of box
= 2 [lb + bh + hl] – lb
= 2[2 × 1.5 + 1.5 × 1 + 1 × 2] – 2 × 1
= 2[3 + 1.5 + 2] – 2
= 2[6.5] – 2
= 13 – 2
= 11 m2
Hence, the required area = 11 m2.
Question 5.
Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m2 of the area is painted. How many cans of paint will she need to paint the room?
Solution:
Surface area of a cuboidal hall without bottom = Total surface area – Area of base
= 2 [lb + bh + hl] – lb
= 2 [15 × 10 + 10 × 7 + 7 × 15] – 15 × 10
= 2[150 + 70 + 105] – 150
= 2 [325] – 150
= 650 – 150
= 500 m2
Area of the paint in one can = 100 m2
![]()
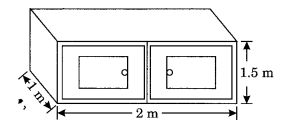
Question 6.
Describe how the two figures at the right are alike and how they are different. Which box has a larger lateral surface area?

Question 8.
The lateral surface area of a hollow cylinder is 4224 cm2. It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of the rectangular sheet.
Solution:
Width of the rectangular sheet = Circumference of the cylinder

h = 128 cm
l = 128 cm, b = 33 cm
Perimeter of the sheet = 2(l + b) = 2(128 + 33) = 2 × 161 = 322 cm
Hence, the required perimeter = 322 cm.
Question 9.
A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.

Solution:
The lateral surface area of the road roller = 2πrh

Hence, the area of road = 1980 m2
Question 10.
A company packages its milk powder in a cylindrical container whose base has a diameter of 14 cm and height 20 cm. The company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label?