Chapter 12 Areas Related to Circles Ex 12.3
Question 1.
Find the area of the shaded region in the given figure, if PQ = 24cm, PR = 7cm and O is the centre of the circle.
Solution:

Question 2.
Find the area of the shaded region in the given figure, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 400.
Solution:
∠AOC = 40° (given)
Radius of the sector AOC = 14 cm

Question 3.
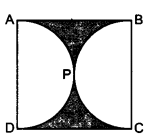
Find the area of the shaded region in the given figure, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
Solution:
ABCD is a square

Question 4.
Find the area of the shaded region in the figure, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
Solution:
Area of the equilateral triangle OAB

Question 5.
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in the figure. Find the area of the remaining portion of the square.
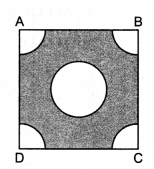
Solution:
Given: side of the square ABCD = 4 cm
Area of the square ABCD = 4 x 4 = 16 cm²
Radius of the quadrant at corner = 1 cm


Question 6.
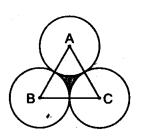
In a circular table cover of the radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in the figure. Find the area of the design (shaded region).
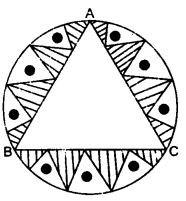
Solution:


Question 7.
In the figure, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
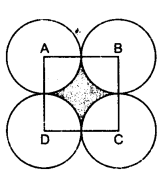
Solution:
Side of the square ABCD = 14 cm
Area of the squat e = (side)² = 14 x 14 = 196²

Question 8.
The given figure depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:

(i) the distance around the track along its inner edge.
(ii) the area of the track.
Solution:
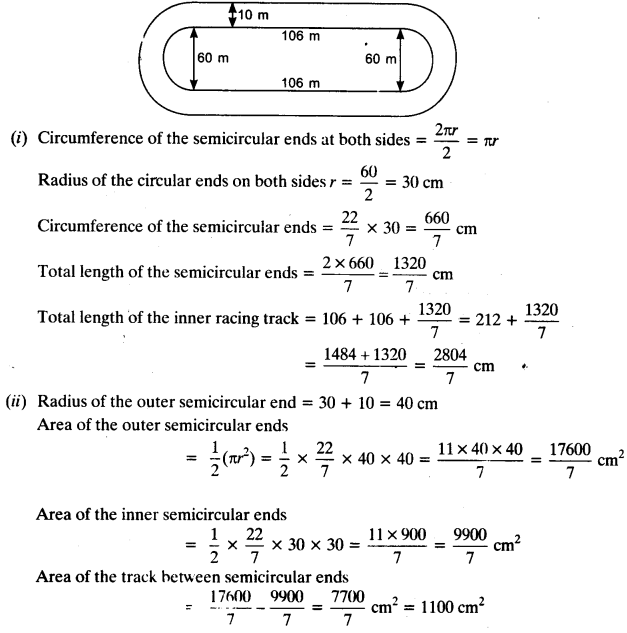
Area of the tracks at both semicircular ends = 2 x 1100 = 2200 cm²
Area of the 2 rectangular portions = 2 x l x h = 2 x 106 x 10 = 2120 cm²
Total area of the track = area of the track at semicircular ends + area of the rectangular portions
= 2200 + 2120 = 4320 cm²
Question 9.
In the figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
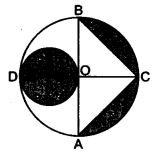
Solution:

Question 10.
The area of an equilateral triangle ABC is 17320.5 cm². With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see figure). Find the area of the shaded region.
(Use π = 3.14 and √3 = 1.73205).
Solution:
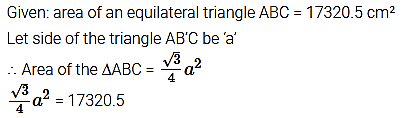


Question 11.
On a square handkerchief, nine circular designs each of the radius 7 cm are made (see figure). Find the area of the remaining portion of the handkerchief.
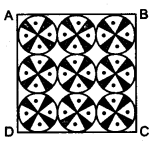
Solution:

Question 12.
In the figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB, (ii) shaded region.
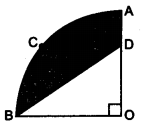
Solution:
(i) Radius of the quadrant OACB = 3.5 cm
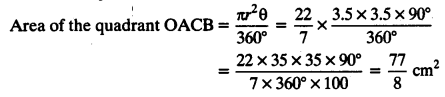
(ii) OD = 2cm and OB = 3.5 cm
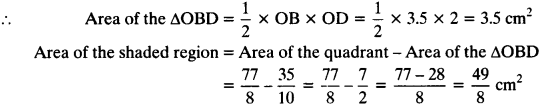
Question 13.
In the figure, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use re = 3.14)
Solution:
Given: side of the square OABC = OA = 20 cm
Area of the square = 20 x 20 = 400 cm²
(Diagonal of the square)² = (side of the square)² + (side of the square)² (By pythagoras theorem)
Diagonal of the square = √2 x (side of the square)
= √2 x (20) = 20√2cm
Radius of the quadrant of circle = Diagonal of square = 202–√
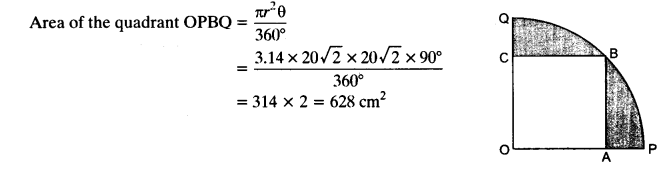
Question 14.
AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see figure). If ∠AOB=30°, find the area of the shaded region.
Solution:
Given: ∠AOB = 30°
Radius of the sector AOB = 21 cm

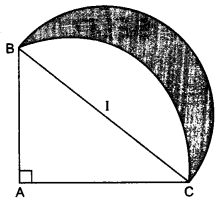
Question 15.
In the figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
Solution:
Radius of the quadrant of the circle = 14 cm

Area of the shaded region = Area of the semicircular region – Area of the region I
= 154 cm² – 56 cm² = 98 cm²
Question 16.
Calculate the area of the designed region in the figure common between the two quadrants of the circles of the radius 8 cm each.
Solution:
Side of the square = 8 cm
Area of the square = 8 x 8 = 64 cm²
Radius of the quadrant (formed at vertex) = 8 cm
