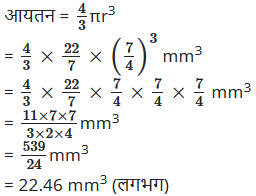Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.8

Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.8

प्रश्न 1.
उस गोले का आयतन ज्ञात कीजिए जिसकी त्रिज्या निम्न है
(i) 7 cm
(ii) 0.63 m
हल:

प्रश्न 2.
उस ठोस गोलाकार गेंद द्वारा हटाए गए (विस्थापित) पानी का आयतन ज्ञात कीजिए, जिसका व्यास निम्न है
(i) 28 cm
(ii) 0.21 m
हल:
(i) गोलाकार गेंद का व्यास (2r) = 28 cm
∴ गेंद की त्रिज्या (r) = 28/2 = 14 cm

गेंद द्वारा विस्थापित पानी का आयतन गेंद के आयतन बराबर होगा।
गेंद का आयतन = 4/3πr³

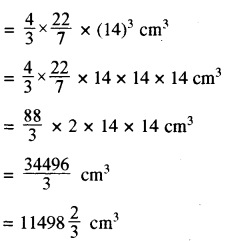
(ii) यहाँ गेंद का व्यास (2r) = 0.21 m
∴ गेंद की त्रिज्या (r) = 0.21/2 m

यहाँ भी गेंद द्वारा विस्थापित पानी का आयतन गेंद के आयतन के समान होगा। अतः
गेंद का आयतन = 4/3πr³

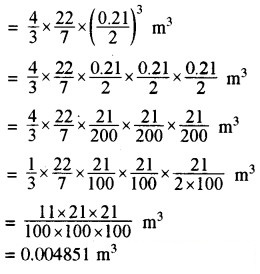
प्रश्न 3.
धातु की एक गेंद का व्यास 4.2 cm है। यदि इस धातु का घनत्व 8.9 ग्राम प्रति cm³ है, तो इस गेंद का द्रव्यमान ज्ञात कीजिए।
हल:

∵ 1 cm³ धातु का द्रव्यमान = 8.9 gm
∴ 38.808 cm³ धातु का द्रव्यमान
= 8.9 × 38.808 gm = 345.3912 gm
= 345.39 gm (लगभग)

प्रश्न 4.
चन्द्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। चन्द्रमा का आयतन पृथ्वी के आयतन की कौनसी भिन्न है?
हल:

इस प्रकार यह कहा जा सकता है कि चन्द्रमा का आयतन पृथ्वी के आयतन का वाँ भाग है।

प्रश्न 5.
व्यास 10.5 cm वाले एक अर्द्धगोलाकार कटोरे में कितने लीटर दूध आ सकता है ?
हल:
प्रश्नानुसार अर्द्धगोलाकार कटोरे का व्यास
(2r) = 10.5 cm
∴ कटोरे की त्रिज्या (r) = 10.5/2 cm = 5.25 cm
हम जानते हैं कि अर्द्धगोलाकार कटोरे में दूध का आयतन उतना ही होगा जितना कि उस कटोरे का आयतन होगा। अतः अर्द्धगोले का आयतन

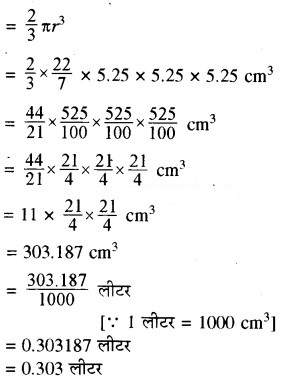
प्रश्न 6.
एक अर्द्धगोलाकार टंकी 1 cm मोटी एक लोहे की चादर (sheet) से बनी है। यदि इसकी आन्तरिक त्रिज्या 1 m है, तो इस टंकी के बनाने में लगे लोहे का आयतन ज्ञात कीजिए।
हल:
प्रश्नानुसार अर्द्धगोलाकार टंकी की आन्तरिक त्रिज्या (r) = 1 m
अर्थात् r = 100 cm
चादर की मोटाई = 1 cm

अतः इस कटोरे की बाह्य त्रिज्या
(R) = 100 + 1 = 101 cm

टंकी को बनाने में प्रयुक्त लोहे का आयतन = बाह्य अर्द्धगोले का आयतन – आन्तरिक अर्द्धगोले का आयतन

प्रश्न 7.
उस गोले का आयतन ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm है।
हल:
प्रश्नानुसार गोले का पृष्ठीय क्षेत्रफल
= 154 cm²

माना कि गोले की त्रिज्या r है। अतः

प्रश्न 8.
किसी भवन का गुम्बद एक अर्द्धगोले के आकार का है। अन्दर से, इसमें सफेदी कराने में 498.96 रुपये व्यय हुए। यदि सफेदी कराने की दर 2 रुपये प्रति वर्ग मीटर है, तो ज्ञात कीजिए
(i) गुम्बद का आन्तरिक वक्र पृष्ठीय क्षेत्रफल
(ii) गुम्बद के अन्दर की हवा का आयतन।
हल:
(i) प्रश्नानुसार सफेदी कराने का कुल व्यय
= 498.96 रु.

तथा सफेदी कराने की दर = 2.00 रु. प्रति m²
∴ सफेदी कराने योग्य कुल क्षेत्रफल

= 498.96/2
= 249.48 m²

∴ गुम्बद का आन्तरिक पृष्ठीय क्षेत्रफल
= 249.48 m²

(ii) माना कि गुम्बद की आन्तरिक त्रिज्या = r
∴ 2πr² = 249.48
या 2 × 22/7 × 2 = 249.48

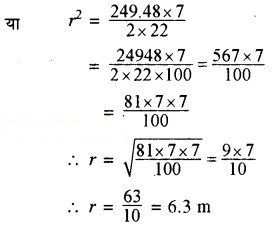
हम समझ सकते हैं कि गुम्बद के अन्दर हवा का आयतन वही होगा जितना कि उस गोलार्द्ध गुम्बद का आयतन होगा अथात् गुम्बद का आयतन

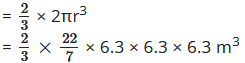
= 44 × 2.1 × 0.9 × 6.3 m³
= 523.9 m³

प्रश्न 9.
लोहे के सत्ताइस ठोस गोलों को पिघलाकर, जिनमें से प्रत्येक की त्रिज्या r है और पृष्ठीय क्षेत्रफल है, एक बड़ा गोला बनाया जाता है जिसका पृष्ठीय क्षेत्रफल S’ है। ज्ञात कीजिए
(i) नए गोले की त्रिज्या r’
(ii) S और S’ का अनुपात।
हल:
प्रश्नानुसार गोलों की संख्या = 27
तथा प्रत्येक गोले की त्रिज्या = r

= 36πr³ …..(i)

इन गोलों को पिघलाकर त्रिज्या का एक नया गोला बनाया गया है। अत: नए गोले का आयतन
समीकरण (i) व (ii) की तुलना करने पर

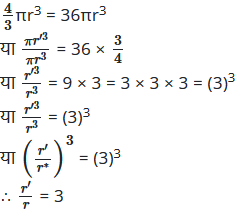
या r’ = 3r
अर्थात् नए गोले की त्रिज्या = 3r
दिए गए प्रश्नानुसार गोले का पृष्ठीय क्षेत्रफल S तथा त्रिज्या r है
∴ S = 4πr² ……(iii)

नए गोले का पृष्ठीय क्षेत्रफल S’ तथा त्रिज्या r’ है
∴ S’ = 4πr’² = 4π(3r)² (∵ r’ = 3r)
∴ S’ = 4π × 3r × 3r
= 36πr² …..(iv)

समीकरण (iii) व (iv) से

अत: S और S’ का अनुपात = 1 : 9

प्रश्न 10.
दवाई का एक कैप्सूल (capsule) 3.5 mm व्यास का एक गोला (गोली) है। इस कैप्सूल को भरने के लिए कितनी दवाई (mm³ में) की आवश्यकता होगी?
हल:
माना कि दवाई के कैप्सूल की त्रिज्या । है।
प्रश्नानुसार व्यास (2r) = 3.5 mm

या r = 20 mm
r = 7 mm

कैप्सूल को भरते समय आवश्यक दवाई की मात्रा उसके आयतन के बराबर होगी अर्थात्