Chapter 14 सांख्यिकी Ex 14.3
प्रश्न 1.
एक संगठन ने पूरे विश्व में 15-44 (वर्षों में ) की आयु वाली महिलाओं में बीमारी और मृत्यु के कारणों का पता लगाने के लिए किए गए सर्वेक्षण से अग्रलिखित आँकड़े (%) प्राप्त किए
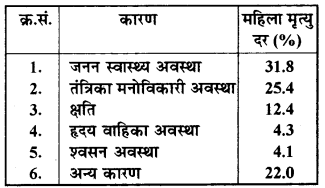
(i) ऊपर दी गई सूचनाओं को आलेखीय रूप में निरूपित कीजिए।
(ii) कौनसी अवस्था पूरे विश्व की महिलाओं के खराब स्वास्थ्य और मृत्यु का बड़ा कारण है?
(iii) अपनी अध्यापिका की सहायता से ऐसे दो कारणों का पता लगाने का प्रयास कीजिए जिनकी ऊपर (ii) में मुख्य भूमिका रही हो।
हल:
(i) हम दी गई सूचना का दण्ड आरेख निम्नलिखित चरणों में बनाते हैं
चरण 1. एक कागज पर हम दो लम्बवत् रेखाएँ OX और OY खींचते हैं।
चरण 2. OX पर हम ‘कारण’ और OY पर महिला मृत्यु दर (%) दिखाते हैं।
चरण 3. OX पर ‘कारण’ दर्शाने के लिए हम एक उपयुक्त चौड़ाई चुनते हैं।
चरण 4. OY पर ‘महिला मृत्यु दर (%)’ को निरूपित करने के लिए हम उपयुक्त पैमाना चुनते हैं।
यहाँ 1 बड़ा खण्ड 5% को निरूपित करता है। इसका दण्ड आलेख निम्न अनुसार है-

(ii) पूरे विश्व में 15-44 (वर्षों में) की आयु वाली महिलाओं की बीमारी और मृत्यु का मुख्य कारण जनन स्वास्थ्य अवस्था है। चूंकि इसका प्रतिशत सबसे ज्यादा है।
(iii) (a) पुनरुत्पादी स्वास्थ्य अवस्था, (b) अपरिपक्व आयु में प्रजनन।
प्रश्न 2.
भारतीय समाज के विभिन्न क्षेत्रों में प्रति हजार लड़कों पर लड़कियों की (निकटतम दस तक की) संख्या के आंकड़े नीचे दिए गए हैं-

(i) ऊपर दी गई सूचनाओं को एक दण्ड आलेख द्वारा निरूपित कीजिए।
(ii) कक्षा में चर्चा करके बताइए कि आप इस आलेख से कौन-कौनसे निष्कर्ष निकाल सकते हैं।
हल:
(i) हम दी गई सूचना का दण्ड आलेख निम्नलिखित चरणों में बनाते हैं
चरण 1. एक कागज पर हम दो लम्बवत् रेखाएँ OX और OY खींचते हैं।
चरण 2. हम OX पर ‘क्षेत्र’ और OY पर ‘प्रति हजार लड़कियों की संख्या’ दिखाते हैं।
चरण 3. OX पर हम प्रत्येक दण्ड के लिए उपयुक्त चौड़ाई चुनते हैं।
चरण 4. हम OY पर उपयुक्त पैमाना चुनते हैं। __ यहाँ 1 बड़ा खण्ड = 100 लड़कियाँ लेते हैं।
चरण 5. हम विभिन्न ऊँचाइयों का परिकलन नीचे दिए अनुसार करते हैं

भारतीय समाज के विभिन्न क्षेत्रों में प्रति हजार लड़कों पर लड़कियों की संख्या

प्रश्न 3.
एक राज्य के विधानसभा के चुनाव में विभिन्न राजनीतिक पार्टियों द्वारा जीती गई सीटों के परिणाम नीचे दिए गए हैं|
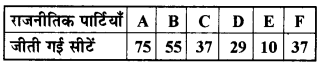
(i) मतदान के परिणामों को निरूपित करने वाला एक दण्ड आलेख खींचिए।
(ii) किस राजनैतिक पार्टी ने अधिकतम सीटें जीती हैं ?
हल:
(i) हम दी गई सूचना का दण्ड आलेख में निरूपण निम्नानुसार करते हैं-.
विधानसभा के चुनावों में विभिन्न राजनीतिक पार्टियों द्वारा जीती गई सीटों के परिणाम।
चुना गया पैमाना: y-अक्ष : 1 बड़ा खण्ड अर्थात् 1 cm = 10 सीटें

(ii) यहाँ पर जीती गई सीटों की संख्या आयतों की ऊँचाई के अनुक्रमानुपाती है और राजनीतिक पार्टी A के लिए प्रदर्शित आयत की ऊँचाई सबसे अधिक है। अतः राजनीतिक पार्टी A ने अधिकतम सीटें जीतीं।
प्रश्न 4.
एक पौधे की 40 पत्तियों की लम्बाइयाँ एक मिलीमीटर तक शुद्ध मापी गई हैं और प्राप्त आँकड़ों को निम्नलिखित सारणी में निरूपित किया गया है-

(i) दिए हुए आंकड़ों को निरूपित करने वाला एक आयतचित्र खींचिए।
(ii) क्या इन्हीं आँकड़ों को निरूपित करने वाला कोई अन्य उपयुक्त आलेख है ?
(iii) क्या यह सही निष्कर्ष है कि 153 मिलीमीटर लम्बाई वाली पत्तियों की संख्या सबसे अधिक है? क्यों?
हल:
(i) हम सबसे पहले बारम्बारता बंटन को सतत बारम्बारता बंटन में बदलेंगे। एक वर्ग की निम्न सीमा और उससे पहले वर्ग की उच्च सीमा का आधा ज्ञात करने पर
1/2(127 – 126) = 1/2 × 1 = 0.5
अब प्रत्येक वर्ग में बंटन को सतत बनाएँगे। प्रत्येक निम्न सीमा में से 0.5 घटाएँगे और प्रत्येक उच्च सीमा में 0.5 जोड़ेंगे।
अत: निम्नानुसार बंटन प्राप्त करते हैं
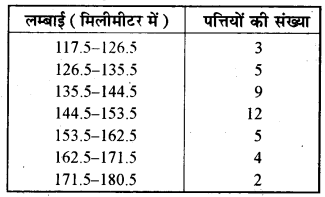
हम दिए हुए आँकड़ों को आयतचित्र के रूप में निम्न अनुसार निरूपित करते हैं-

पत्तों की लम्बाइयों का एक मिलीमीटर तक शुद्ध माप
चुना गया पैमाना: Y-अक्ष पर एक बड़ा खण्डअर्थात् 1 cm = 1 पत्ता।
X-अक्ष पर एक खण्ड = 9
(ii) हाँ, इन्हीं आँकड़ों को निरूपित करने की एक _अन्य उपयुक्त विधि बारम्बारता बहुभुज है।
(iii) नहीं, वर्ग (144:5-153.5) मिमी. के अन्तर्गत 153 मिमी. आता है, अत: इस वर्ग की बारम्बारता सबसे अधिक है परन्तु यह आवश्यक नहीं है कि 153 मिमी लम्बाई की पत्तियों की संख्या सबसे अधिक हो; क्योंकि यह अधिकतम बारम्बारता 144.5 मिमी. से 153.5 मिमी. तक के पूरे वर्ग का प्रतिनिधित्व करती है न कि मात्र 153 मिमी. का।
प्रश्न 5.
नीचे की सारणी में 400 नियॉन लैम्पों के जीवन काल दिए गए हैं|
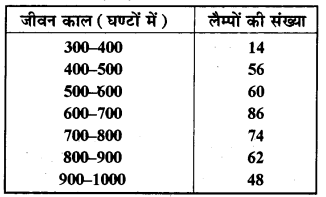
(i) एक आयतचित्र की सहायता से दी हुई सूचनाओं को निरूपित कीजिए।
(ii) कितने लैम्पों के जीवन काल 700 घण्टों से अधिक हैं?
हल:
(i) हम दी गई सूचना को निम्नानुसार आयतचित्र में निरूपित करते हैं-

(ii) 700 घण्टों से अधिक जीवन काल वाले लैम्पों की संख्या
= 74 + 62 + 48
= 184 लैम्प उत्तर
प्रश्न 6.
नीचे की दो सारणियों में प्राप्त किए गए अंकों के अनुसार दो सेक्शनों के विद्यार्थियों का बंटन दिया गया है-
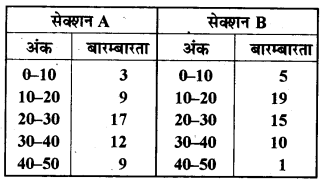
दो बारम्बारता बहुभुजों की सहायता से एक ही आलेख पर दोनों सेक्शनों के विद्यार्थियों के प्राप्तांक निरूपित कीजिए। दोनों बहभुजों का अध्ययन करके दोनों सेक्शनों के निष्पादनों की तुलना कीजिए।
हल:
दी गई सूचना को बारम्बारता बहुभुज के रूप में निरूपित करेंगे। अतः हम वर्ग-चिह्न और संगत सेक्शन A और B की बारम्बारताओं की सारणी बनाते हैं।
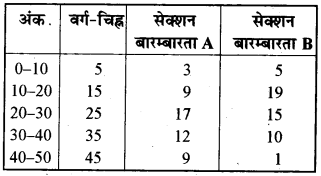
हम x-अक्ष पर वर्ग-चिह्न और y-अक्ष पर विद्यार्थियों की संख्या दर्शाते हैं।

सेक्शन A को बारम्बारता बहुभुज के लिए हम क्रमित युग्मों (5, 3), (15, 9), (25, 17), (35, 12) और (45, 9) को बिन्दुओं द्वारा आलेखित करते हैं।
बिन्दुओं को रेखाखण्डों द्वारा मिलाने पर हमें सेक्शन A का बारम्बारता बहुभुज प्राप्त होता है। हम क्रमित युग्म (5, 5), (15, 19), (25, 15), (35, 10) और (45, 1) को आलेखित करते हैं।
इनको रेखाखण्डों से जोड़ने पर हमें सेक्शन B का बारम्बारता बहुभुज प्राप्त होता है।
प्रश्न 7.
एक क्रिकेट मैच में दो टीमों A और B द्वारा प्रथम 60 गेंदों में बनाए गए रन आगे दिए गए हैं-

बारम्बारता बहुभुजों की सहायता से एक ही आलेख पर दोनों टीमों के आंकड़े निरूपित कीजिए।
(संकेत : पहले वर्ग अन्तरालों को संतत बनाइए)
हल:
(1) दिये हुये वर्ग असतत हैं। प्रत्येक वर्ग की निम्न सीमा में 0.5 घटाकर और ऊपरी सीमा में 0.5 जोड़कर इन्हें सतत बनायेंगे, क्योंकि एक वर्ग की निम्न सीमा और उससे पहले वर्ग की उच्च सीमा का अन्तर एक है। अतः बारम्बारता वितरण को लगातार बनाने के लिये प्रत्येक निम्न सीमा में से n/2 = 1/2 = 0.5 घटायेंगे और प्रत्येक उच्च सीमा में 0.5 जोड़ेंगे।
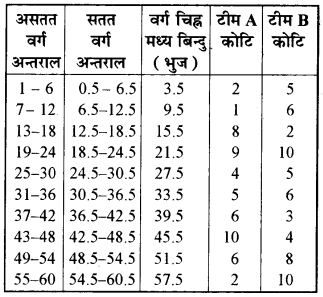
(2) अत: दोनों टीमों के निर्देशांक निम्न होंगेटीम A के
(3.5, 2), (9.5, 1), (15.5, 8), (21.5, 9), (27.5, 4), (33.5, 5), (39.5, 6), (45.5, 10), (51.5, 6) तथा (57.5, 2)
टीम B के
(3.5, 5), (9.5, 6), (15.5, 2), (21.5, 10), (27.5, 5), (33.5, 6), (39.5, 3), (45.5, 4), (51.5, 8) तथा (57.5, 10)
(3) X-अक्ष पर उचित पैमाना लेकर वर्गों की सीमाओं को प्रदर्शित किया।
(4) Y-अक्ष पर टीमों द्वारा बनाये गये रनों को उचित पैमाना लेकर अंकित किया।

(5) प्रथम वर्ग (0.5-6.5) के ठीक पूर्व एक कल्पित | वर्ग लेकर उसका मध्य बिन्दु A ज्ञात किया।
(6) अन्तिम वर्ग (54.5-60.5) के ठीक पश्चात् एक कल्पित वर्ग लेकर उसका मध्य बिन्दु L को ज्ञात किया।
प्रश्न 8.
एक पार्क में खेल रहे विभिन्न आयु वर्गों के बच्चों की संख्या का एक यादृच्छिक सर्वेक्षण (random survey) करने पर निम्नलिखित आँकड़े प्राप्त हुए-

ऊपर दिए आँकड़ों को निरूपित करने वाला एक आयतचित्र खींचिए।
हल:
यहाँ वर्ग आकार बराबर आकार का नहीं है। हम न्यूनतम वर्ग आकार क़ा वर्ग चुनते हैं। यहाँ न्यूनतम वर्ग आकार 1 है।
इस वर्ग आकार के अनुसार समायोजित बारम्बारता (आयतों की ऊँचाइयों) की निम्न सारणी प्राप्त होती है।

अब हम इन लम्बाइयों का प्रयोग करके आयतचित्र बनाते हैं।

प्रश्न 9.
एक स्थानीय टेलीफोन निर्देशिका से 100 कुलनाम (surname) यदृच्छया लिए गए और उनसे अंग्रेजी वर्णमाला के अक्षरों की संख्या का निम्न बारम्बारता बंटन प्राप्त किया गया-
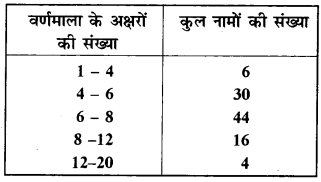
(i) दी हुई सूचनाओं को निरूपित करने वाला एक आयतचित्र खींचिए।
(ii) वह वर्ग अन्तराल बताइए जिसमें अधिकतम संख्या में कुल नाम हैं।
हल:
यहाँ वर्ग आकार बराबर नहीं है। हम न्यूनतम वर्ग आकार का वर्ग चुनते हैं । यहाँ न्यूनतम वर्ग आकार 2 है।
इस वर्ग आकार के अनुसार समायोजित बारम्बारता (आयतों की ऊँचाइयाँ) की निम्न सारणी प्राप्त होती है।
अब हम इन लम्बाइयों का प्रयोग करके आयतचित्र बनाते हैं-

Chapter 14 सांख्यिकी Ex 14.3
प्रश्न 1.
एक संगठन ने पूरे विश्व में 15-44 (वर्षों में ) की आयु वाली महिलाओं में बीमारी और मृत्यु के कारणों का पता लगाने के लिए किए गए सर्वेक्षण से अग्रलिखित आँकड़े (%) प्राप्त किए 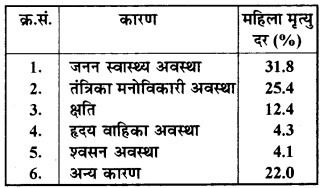
(i) ऊपर दी गई सूचनाओं को आलेखीय रूप में निरूपित कीजिए।
(ii) कौनसी अवस्था पूरे विश्व की महिलाओं के खराब स्वास्थ्य और मृत्यु का बड़ा कारण है?
(iii) अपनी अध्यापिका की सहायता से ऐसे दो कारणों का पता लगाने का प्रयास कीजिए जिनकी ऊपर (ii) में मुख्य भूमिका रही हो।
हल:
(i) हम दी गई सूचना का दण्ड आरेख निम्नलिखित चरणों में बनाते हैं
चरण 1. एक कागज पर हम दो लम्बवत् रेखाएँ OX और OY खींचते हैं।
चरण 2. OX पर हम ‘कारण’ और OY पर महिला मृत्यु दर (%) दिखाते हैं।
चरण 3. OX पर ‘कारण’ दर्शाने के लिए हम एक उपयुक्त चौड़ाई चुनते हैं।
चरण 4. OY पर ‘महिला मृत्यु दर (%)’ को निरूपित करने के लिए हम उपयुक्त पैमाना चुनते हैं।
यहाँ 1 बड़ा खण्ड 5% को निरूपित करता है। इसका दण्ड आलेख निम्न अनुसार है- 
(ii) पूरे विश्व में 15-44 (वर्षों में) की आयु वाली महिलाओं की बीमारी और मृत्यु का मुख्य कारण जनन स्वास्थ्य अवस्था है। चूंकि इसका प्रतिशत सबसे ज्यादा है।
(iii) (a) पुनरुत्पादी स्वास्थ्य अवस्था, (b) अपरिपक्व आयु में प्रजनन।
प्रश्न 2.
भारतीय समाज के विभिन्न क्षेत्रों में प्रति हजार लड़कों पर लड़कियों की (निकटतम दस तक की) संख्या के आंकड़े नीचे दिए गए हैं- 
(i) ऊपर दी गई सूचनाओं को एक दण्ड आलेख द्वारा निरूपित कीजिए।
(ii) कक्षा में चर्चा करके बताइए कि आप इस आलेख से कौन-कौनसे निष्कर्ष निकाल सकते हैं।
हल:
(i) हम दी गई सूचना का दण्ड आलेख निम्नलिखित चरणों में बनाते हैं
चरण 1. एक कागज पर हम दो लम्बवत् रेखाएँ OX और OY खींचते हैं।
चरण 2. हम OX पर ‘क्षेत्र’ और OY पर ‘प्रति हजार लड़कियों की संख्या’ दिखाते हैं।
चरण 3. OX पर हम प्रत्येक दण्ड के लिए उपयुक्त चौड़ाई चुनते हैं।
चरण 4. हम OY पर उपयुक्त पैमाना चुनते हैं। __ यहाँ 1 बड़ा खण्ड = 100 लड़कियाँ लेते हैं।
चरण 5. हम विभिन्न ऊँचाइयों का परिकलन नीचे दिए अनुसार करते हैं

भारतीय समाज के विभिन्न क्षेत्रों में प्रति हजार लड़कों पर लड़कियों की संख्या 
प्रश्न 3.
एक राज्य के विधानसभा के चुनाव में विभिन्न राजनीतिक पार्टियों द्वारा जीती गई सीटों के परिणाम नीचे दिए गए हैं| 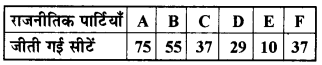
(i) मतदान के परिणामों को निरूपित करने वाला एक दण्ड आलेख खींचिए।
(ii) किस राजनैतिक पार्टी ने अधिकतम सीटें जीती हैं ?
हल:
(i) हम दी गई सूचना का दण्ड आलेख में निरूपण निम्नानुसार करते हैं-.
विधानसभा के चुनावों में विभिन्न राजनीतिक पार्टियों द्वारा जीती गई सीटों के परिणाम।
चुना गया पैमाना: y-अक्ष : 1 बड़ा खण्ड अर्थात् 1 cm = 10 सीटें 
(ii) यहाँ पर जीती गई सीटों की संख्या आयतों की ऊँचाई के अनुक्रमानुपाती है और राजनीतिक पार्टी A के लिए प्रदर्शित आयत की ऊँचाई सबसे अधिक है। अतः राजनीतिक पार्टी A ने अधिकतम सीटें जीतीं।
प्रश्न 4.
एक पौधे की 40 पत्तियों की लम्बाइयाँ एक मिलीमीटर तक शुद्ध मापी गई हैं और प्राप्त आँकड़ों को निम्नलिखित सारणी में निरूपित किया गया है- 
(i) दिए हुए आंकड़ों को निरूपित करने वाला एक आयतचित्र खींचिए।
(ii) क्या इन्हीं आँकड़ों को निरूपित करने वाला कोई अन्य उपयुक्त आलेख है ?
(iii) क्या यह सही निष्कर्ष है कि 153 मिलीमीटर लम्बाई वाली पत्तियों की संख्या सबसे अधिक है? क्यों?
हल:
(i) हम सबसे पहले बारम्बारता बंटन को सतत बारम्बारता बंटन में बदलेंगे। एक वर्ग की निम्न सीमा और उससे पहले वर्ग की उच्च सीमा का आधा ज्ञात करने पर
1/2(127 – 126) = 1/2 × 1 = 0.5
अब प्रत्येक वर्ग में बंटन को सतत बनाएँगे। प्रत्येक निम्न सीमा में से 0.5 घटाएँगे और प्रत्येक उच्च सीमा में 0.5 जोड़ेंगे।
अत: निम्नानुसार बंटन प्राप्त करते हैं 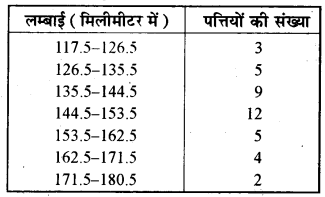
हम दिए हुए आँकड़ों को आयतचित्र के रूप में निम्न अनुसार निरूपित करते हैं- 
पत्तों की लम्बाइयों का एक मिलीमीटर तक शुद्ध माप
चुना गया पैमाना: Y-अक्ष पर एक बड़ा खण्डअर्थात् 1 cm = 1 पत्ता।
X-अक्ष पर एक खण्ड = 9
(ii) हाँ, इन्हीं आँकड़ों को निरूपित करने की एक _अन्य उपयुक्त विधि बारम्बारता बहुभुज है।
(iii) नहीं, वर्ग (144:5-153.5) मिमी. के अन्तर्गत 153 मिमी. आता है, अत: इस वर्ग की बारम्बारता सबसे अधिक है परन्तु यह आवश्यक नहीं है कि 153 मिमी लम्बाई की पत्तियों की संख्या सबसे अधिक हो; क्योंकि यह अधिकतम बारम्बारता 144.5 मिमी. से 153.5 मिमी. तक के पूरे वर्ग का प्रतिनिधित्व करती है न कि मात्र 153 मिमी. का।
प्रश्न 5.
नीचे की सारणी में 400 नियॉन लैम्पों के जीवन काल दिए गए हैं| 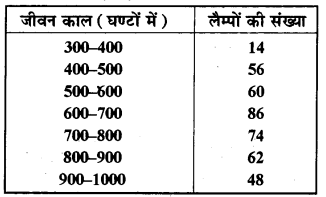
(i) एक आयतचित्र की सहायता से दी हुई सूचनाओं को निरूपित कीजिए।
(ii) कितने लैम्पों के जीवन काल 700 घण्टों से अधिक हैं?
हल:
(i) हम दी गई सूचना को निम्नानुसार आयतचित्र में निरूपित करते हैं- 
(ii) 700 घण्टों से अधिक जीवन काल वाले लैम्पों की संख्या
= 74 + 62 + 48
= 184 लैम्प उत्तर
प्रश्न 6.
नीचे की दो सारणियों में प्राप्त किए गए अंकों के अनुसार दो सेक्शनों के विद्यार्थियों का बंटन दिया गया है- 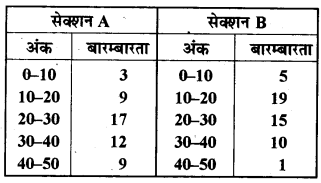
दो बारम्बारता बहुभुजों की सहायता से एक ही आलेख पर दोनों सेक्शनों के विद्यार्थियों के प्राप्तांक निरूपित कीजिए। दोनों बहभुजों का अध्ययन करके दोनों सेक्शनों के निष्पादनों की तुलना कीजिए।
हल:
दी गई सूचना को बारम्बारता बहुभुज के रूप में निरूपित करेंगे। अतः हम वर्ग-चिह्न और संगत सेक्शन A और B की बारम्बारताओं की सारणी बनाते हैं। 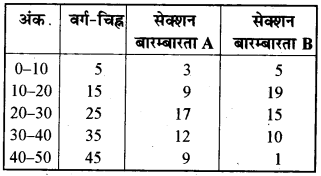
हम x-अक्ष पर वर्ग-चिह्न और y-अक्ष पर विद्यार्थियों की संख्या दर्शाते हैं। 
सेक्शन A को बारम्बारता बहुभुज के लिए हम क्रमित युग्मों (5, 3), (15, 9), (25, 17), (35, 12) और (45, 9) को बिन्दुओं द्वारा आलेखित करते हैं।
बिन्दुओं को रेखाखण्डों द्वारा मिलाने पर हमें सेक्शन A का बारम्बारता बहुभुज प्राप्त होता है। हम क्रमित युग्म (5, 5), (15, 19), (25, 15), (35, 10) और (45, 1) को आलेखित करते हैं।
इनको रेखाखण्डों से जोड़ने पर हमें सेक्शन B का बारम्बारता बहुभुज प्राप्त होता है।
प्रश्न 7.
एक क्रिकेट मैच में दो टीमों A और B द्वारा प्रथम 60 गेंदों में बनाए गए रन आगे दिए गए हैं- 
बारम्बारता बहुभुजों की सहायता से एक ही आलेख पर दोनों टीमों के आंकड़े निरूपित कीजिए।
(संकेत : पहले वर्ग अन्तरालों को संतत बनाइए)
हल:
(1) दिये हुये वर्ग असतत हैं। प्रत्येक वर्ग की निम्न सीमा में 0.5 घटाकर और ऊपरी सीमा में 0.5 जोड़कर इन्हें सतत बनायेंगे, क्योंकि एक वर्ग की निम्न सीमा और उससे पहले वर्ग की उच्च सीमा का अन्तर एक है। अतः बारम्बारता वितरण को लगातार बनाने के लिये प्रत्येक निम्न सीमा में से n/2 = 1/2 = 0.5 घटायेंगे और प्रत्येक उच्च सीमा में 0.5 जोड़ेंगे। 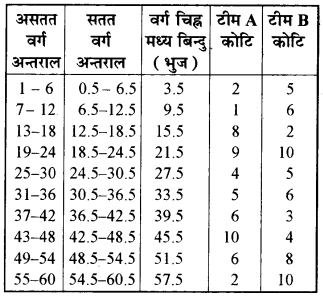
(2) अत: दोनों टीमों के निर्देशांक निम्न होंगेटीम A के
(3.5, 2), (9.5, 1), (15.5, 8), (21.5, 9), (27.5, 4), (33.5, 5), (39.5, 6), (45.5, 10), (51.5, 6) तथा (57.5, 2)
टीम B के
(3.5, 5), (9.5, 6), (15.5, 2), (21.5, 10), (27.5, 5), (33.5, 6), (39.5, 3), (45.5, 4), (51.5, 8) तथा (57.5, 10)
(3) X-अक्ष पर उचित पैमाना लेकर वर्गों की सीमाओं को प्रदर्शित किया।
(4) Y-अक्ष पर टीमों द्वारा बनाये गये रनों को उचित पैमाना लेकर अंकित किया। 
(5) प्रथम वर्ग (0.5-6.5) के ठीक पूर्व एक कल्पित | वर्ग लेकर उसका मध्य बिन्दु A ज्ञात किया।
(6) अन्तिम वर्ग (54.5-60.5) के ठीक पश्चात् एक कल्पित वर्ग लेकर उसका मध्य बिन्दु L को ज्ञात किया।
प्रश्न 8.
एक पार्क में खेल रहे विभिन्न आयु वर्गों के बच्चों की संख्या का एक यादृच्छिक सर्वेक्षण (random survey) करने पर निम्नलिखित आँकड़े प्राप्त हुए- 
ऊपर दिए आँकड़ों को निरूपित करने वाला एक आयतचित्र खींचिए।
हल:
यहाँ वर्ग आकार बराबर आकार का नहीं है। हम न्यूनतम वर्ग आकार क़ा वर्ग चुनते हैं। यहाँ न्यूनतम वर्ग आकार 1 है।
इस वर्ग आकार के अनुसार समायोजित बारम्बारता (आयतों की ऊँचाइयों) की निम्न सारणी प्राप्त होती है। 
अब हम इन लम्बाइयों का प्रयोग करके आयतचित्र बनाते हैं। 
प्रश्न 9.
एक स्थानीय टेलीफोन निर्देशिका से 100 कुलनाम (surname) यदृच्छया लिए गए और उनसे अंग्रेजी वर्णमाला के अक्षरों की संख्या का निम्न बारम्बारता बंटन प्राप्त किया गया- 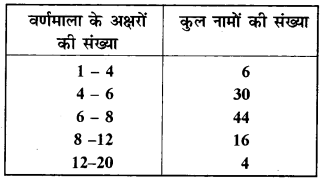
(i) दी हुई सूचनाओं को निरूपित करने वाला एक आयतचित्र खींचिए।
(ii) वह वर्ग अन्तराल बताइए जिसमें अधिकतम संख्या में कुल नाम हैं।
हल:
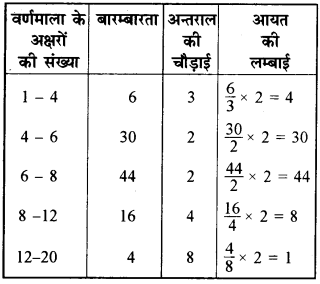
यहाँ वर्ग आकार बराबर नहीं है। हम न्यूनतम वर्ग आकार का वर्ग चुनते हैं । यहाँ न्यूनतम वर्ग आकार 2 है।
इस वर्ग आकार के अनुसार समायोजित बारम्बारता (आयतों की ऊँचाइयाँ) की निम्न सारणी प्राप्त होती है। 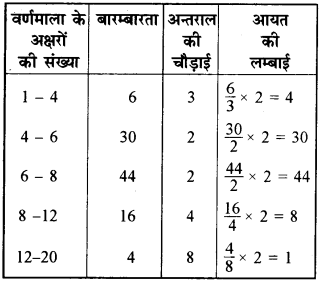
अब हम इन लम्बाइयों का प्रयोग करके आयतचित्र बनाते हैं- 