Chapter 14 सांख्यिकी Ex 14.4
प्रश्न 1.
एक टीम ने फुटबाल के 10 मैचों में निम्नलिखित गोल किए
2, 3, 4, 5, 0, 1, 3, 3, 4, 3
इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
हल:
हम जानते हैं कि
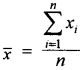

बहुलक के लिए बारम्बारता सारणी बनाने पर

सारणी के अनुसार गोलों की अधिकतम संख्या 4 है अतः बहुलक = 3
प्रश्न 2.
गणित की परीक्षा में 15 विद्यार्थियों ने (100 में से) निम्नलिखित अंक प्राप्त किए
41, 39, 48, 52, 46, 62, 54, 40, 96,52, 98, 40, 42, 52,60
इन आँकड़ों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
हल:
माध्य के लिए
हम जानते हैं कि

∴ x̄ = 54.8 उत्तर
माध्यक के लिए-प्रदत्तों को आरोही क्रम में लिखने पर –
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62,.96, 98
यहाँ n = 15 जो कि एक विषम संख्या है।

बहुलक के लिए-बारम्बारता सारणी बनाने पर

सारणी के अनुसार अंक 52 की बारम्बारता सबसे अधिक 3 है अतः बहुलक = 52
प्रश्न 3.
निम्नलिखित प्रेक्षणों को आरोही क्रम में व्यवस्थित किया गया है। यदि आँकड़ों का माध्यक 63 हो, तो x का मान ज्ञात कीजिए
29, 32, 48, 50, x, x+2, 72, 78,84, 95
हल:
प्रदत्तों को आरोही क्रम में व्यवस्थित करने पर हम देखते हैं कि ये आँकड़े व्यवस्थित हैं तथा n = 10 एक सम संख्या है।

प्रश्न 4.
आँकड़ों 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18 का बहुलक ज्ञात कीजिए।
हल:
दिए गए आँकड़ों की बारम्बारता सारणी बनाने पर

सारणी से ज्ञात होता है कि यहाँ प्रेक्षण 14 की अधिकतम बारम्बारता 4 है। अत: बहुलक = 14
प्रश्न 5.
अग्र सारणी से एक फैक्टरी में काम कर रहे 60 कर्मचारियों का माध्य वेतन ज्ञात कीजिए

हल:

= 305000/60
∴ x̄ = 5083.33
अर्थात् कर्मचारियों का माध्य वेतन 5083.33 रु. है।
प्रश्न 6.
निम्न स्थिति पर आधारित एक उदाहरण दीजिए
(i) माध्य ही केन्द्रीय प्रवृत्ति का उपयुक्त माप है।
(ii) माध्य केन्द्रीय प्रवृत्ति का उपयुक्त माप नहीं है, जबकि माध्यक एक उपयुक्त माप है।
हल:
(i) इसे स्पष्ट करने के लिए हम निम्नलिखित उदाहरण लेते हैं
उदाहरण – यदि कक्षा IX के गणित विषय में दस छात्रों के प्राप्तांक 52, 75, 40, 70, 43, 40, 65, 35, 48, 52 हों तो समान्तर माध्य ज्ञात कीजिए।

इसका माध्यक –
आरोही क्रम-35, 40, 40, 43, 48, 52, 52, 65, 70, 75
∴ माध्यक = 10 + 1 = 5.5
अर्थात् 5वें व 6वें पद का माध्य
![]()
तथा बहुलक 40 व 52 है। इस प्रकार हम देखते हैं कि 52 अंक 10 विद्यार्थियों के प्रदर्शन को निरूपित करता है परन्तु माध्यक या बहुलक नहीं। इसी कारण माध्य केन्द्रीय प्रवृत्ति का उपयुक्त माप है क्योंकि इसके परिकलन में प्रत्येक पद लिया जाता है जिससे यह प्रत्येक प्रदत्त द्वारा प्रभावित होता है।
(ii) माध्यक चरम मानों से प्रभावित नहीं होता है जबकि माध्य चरम मानों से बहुत प्रभावित होता है। जैसे

यदि इसमें दो मान 250 व 500 जोड़ दें तो माध्य 87.4 प्राप्त होगा जबकि माध्यक 4.5 होगा। यहाँ माध्य में बहुत परिवर्तन लेकिन माध्यक में बहुत कम परिवर्तन हुआ। अत: यह कहा जा सकता है कि माध्यक ही केन्द्रीय प्रवृत्ति का उपयुक्त माप है।