Chapter 16 Playing with Numbers Exercise 16.1
Find the values of the letters in each of the following and give reasons for the steps involved.
Question 1.
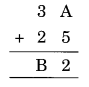
Solution:

Question 2.
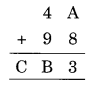
Solution:
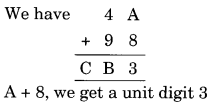

Question 3.

Solution:
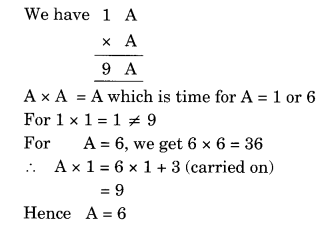
Question 4.

Solution:
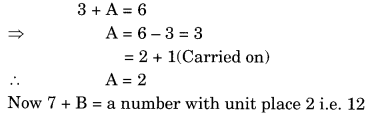
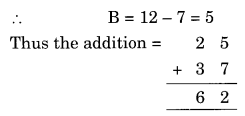
Question 5.
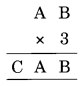
Solution:
3 × B = B
⇒ B = D
3 × A = CA
⇒ 3 × 5 = 15
Thus A = 5 and C = 1
Hence A = 5, B = 0 and C = 1
Question 6.

Solution:
5 × B = B
⇒ B = 0 or 5
5 × A = CA
5 × 5 = 25
Only possible when B = 0
Thus A = 5 and C = 2
Hence A = 5, B = 0 and C = 2
Question 7.
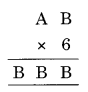
Solution:
B × 6 = B
6 × 4 = 24 → B = 4 and 2 is carried to
6 × A = BB
⇒ 6 × 7 = 42 + 2 (carried on) = 44
Thus B = 7
Hence A = 7 and B = 4
Question 8.

Solution:
1 + B = 0
1 + 9 = 10 → unit digit is 0 and 1 is carried to A
+ 1 +1 (carried on) = B = 9
A + 2 = 9 ⇒ A = 9 – 2 = 7
Hence A = 7 and B = 9
Question 9.
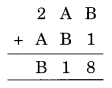
Solution:
B + 1 = 8 ⇒ B = 8 – 1 = 7
A + B = a number with unit digit 1
A + B = 11
⇒ A + 7 = 11
⇒ A = 11 – 7 = 4 (1 Carried to)
Now 1 carried on + 2 + A = B
3 + A = 7
⇒ A = 7 – 3 = 4
Hence A = 4, B = 7
Question 10.

Solution:
9 = A + B
9 = 1 + 8 or 2 + 7 or 3 + 6 or 4 + 5 or 8 + 1 or 7 + 2 or 6 + 3 or 5 + 4 or 0 + 9 or 9 + 0
Now 0 is required at unit place
2 + A = 10
⇒ A = 10 – 2 = 8
B = 9 – 8 = 1
1 + 6 + 1 (carried on) = A = 8
Hence A = 8 and B = 1







