Chapter 2 बहुपद Ex 2.2

Chapter 2 बहुपद Ex 2.2

प्रश्न 1.
निम्न द्विघात बहुपदों के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच सम्बन्ध की सत्यता की जाँच कीजिए :
(i) x² – 2x – 8
हल-
प्रश्नानुसार
x² – 2x – 8 = x² + 2x – 4x – 8
= x(x + 2) – 4(x + 2)
= (x + 2) (x – 4)
x² – 2x – 8 का मान शून्य होगा यदि (x + 2) (x – 4) के मान शून्य हों।
अर्थात् x + 2 = 0 या x – 4 = 0
अर्थात् x = -2 या x = 4
अत: x² – 2x – 8 के शून्यक -2 और 4 हैं।
अब, शून्यकों का योग = (-2) + 4 = 2

(ii) 4s² – 4s + 1
हल-
प्रश्नानुसार 4s² – 4s + 1 = 4s² – 2s – 2s + 1
= 2s(2s – 1) – 1 (2s – 1)
= (2s – 1) (2s – 1)
अतः, 4s² – 4s + 1 का मान शून्य होगा यदि (2s – 1) (2s – 1) का मान शून्य हो।
अर्थात् 2s – 1 = 0 या 2s – 1 = 0, यानी

(iii) 6x² – 3 – 7x
हल-
प्रश्नानुसार 6x² – 3 – 7x = 6x² – 7x – 3
= 6x² – 9x + 2x – 3
= 3x(2x – 3) + 1(2x – 3)
= (3x + 1) (2x – 3)
अतः, 6x² – 3 – 7x का मान शून्य होगा यदि (3x + 1) (2x – 3) का मान शून्य हो।
अर्थात् 3x + 1 = 0 या 2x – 3 = 0,

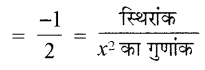
(iv) 4u² + 8u
हल-
प्रश्नानुसार 4u² + 8u = 4u(u + 2)
अतः 4u² + 8u का मान शून्य होगा यदि 4u(u + 2) का मान शून्य है।
यानी u = 0 या u + 2 = 0, यानी u = 0 या u = -2
अतः, 4u² + 8u के शून्यक 0 और -2 हैं।
अब शून्यकों का योग = 0 + (-2) = -2

(v) t² – 15
हल-
प्रश्नानुसार t² – 15 = (t – √15) (t + √15)
अत: t² – 15 का मान शून्य होगा जब (t – √15)(t + √15) का मान शून्य हो।
अर्थात् t – √15 = 0 या t + √15 = 0,
यानी t = +√15 या t = -√15
अतः, t² – 15 के शून्यक √15 और -√15 हैं।
अब, शून्यकों का योग = √15 + (-√15)

(vi) 3x² – x – 4
हल-
प्रश्नानुसार 3x² – x – 4 = 3x² + 3x – 4x – 4
= 3x(x + 1) – 4(x + 1)
= (x + 1) (3x – 4)
3x² – x – 4 का मान शून्य होगा जब (x + 1) (3x – 4) का मान शून्य हो।
अर्थात् x + 1 = 0 या 3x – 4 = 0,

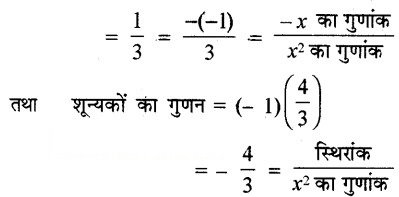
प्रश्न 2.
एक द्विघात बहुपदं ज्ञात कीजिए, जिनके शून्यकों का योग तथा गुणनफल क्रमशः दी गई संख्याएँ हैं :