Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.5

Chapter 3 दो चरों वाले रैखिक समीकरण युग्म Ex 3.5

प्रश्न 1.
निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं। अद्वितीय हल की स्थिति में, उसे वज्रगुणन विधि से ज्ञात कीजिए-
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0
हल-
दिया गया रैखिक समीकरण-युग्म है :
x – 3y – 3 = 0
और 3x – 9y – 2 = 0
यहाँ a₁ = 1, b₁ = -3, c₁ = -3
a₂ = 3, b₂ = -9, c₂ = -2

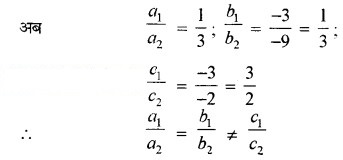
अतः, दी गई समीकरण निकाय का कोई हल नहीं है।

(ii) 2x + y = 5
3x + 2y = 8
हल-
दिया गया रैखिक समीकरण-युग्म है :
2x + y = 5
और 3x + 2y = 8
या 2x + y – 5 = 0
और 3x + 2y – 8 = 0
यहाँ a₁ = 2, b₁ = 1, c₁ = -5
a₂ = 3, b₂ = 2, c₂ = -8

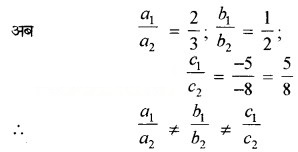
∴ दिए गए समीकरण निकाय का एक अद्वितीय हल है।
तब वज्रगुणन से,

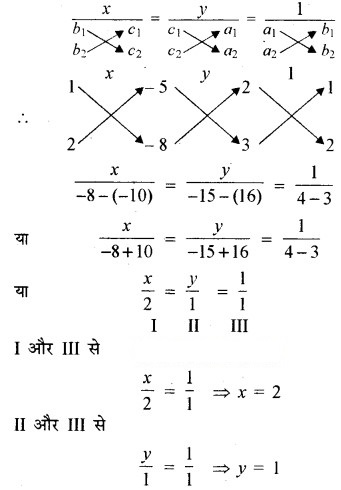
अतः, x = 2 और y = 1

(iii) 3x – 5y = 20
6x – 10y = 40
हल-
दिया गया रैखिक समीकरण-युग्म है :
3x – 5y = 20
और 6x – 10y = 40
या 3x – 5y – 20 = 0
और 6x – 10y – 40 = 0
यहाँ a₁ = 3, b₁ = -5, c₁ = -20
a₂ = 6, b₂ = -10, c₂ = -40

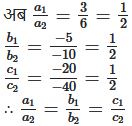
अतः दी गई समीकरण निकाय के अपरिमित रूप से अनेक हल हैं।

(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0
हल-
दिया गया रैखिक समीकरण युग्म है :
x – 3y – 7 = 0
और 3x – 3y – 15 = 0
यहाँ a₁ = 1, b₁ = -3, c₁ = -7
a₂ = 3, b₂ = -3, c₂ = -15

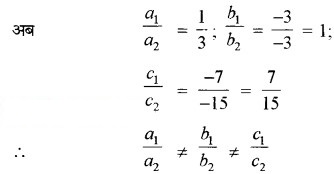
∴ दिए गए समीकरण निकाय का एक अद्वितीय हल हैं।
तब वज्रगुणन विधि से हल करने पर

II और III से,

यहाँ x = 4, y = -1

प्रश्न 2.
(i) a और b के किन मानों के लिए निम्न रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होंगे?
2x + 3y = 7
(a – b)x + (a + b)y = 3a + b – 2
हल-
दी गई रैखिक समीकरण युग्म है :
2x + 3y = 7
और (a – b)x + (a + b)y = 3a + b – 2
या 2x + 3y – 7 = 0
और (a – b)x + (a + b)y – (3a + b – 2) = 0
यहाँ a₁ = 2, b₁ = 3, c₁ = -7
a₂ = a – b, b₂ = a + b, c₂ = -(3a + b – 2)
∴ दी गई समीकरण निकाय के अपरिमित रूप से अनेक हल हैं :

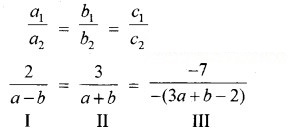
I और III से,

या 6a + 2b – 4 = 7a – 7b
या -a + 9b – 4 = 0
या a = 9b – 4 ……(1)
II और III से,

या 9a + 3b – 6 = 7a + 7b
या 2a – 4b – 6 = 0
या a – 2b – 3 = 0 ……(2)
समीकरण (1) से a का मान (2) में प्रतिस्थापित करने पर
9b – 4 – 2b – 3 = 0
या 7b – 7 = 0
या 7b = 7
या b = 1
b के इस मान को (1) में प्रतिस्थापित करने पर
a = 9 × 1 – 4 = 9 – 4
a = 5
अतः रैखिक समीकरण युग्म के अभीष्ट हल a = और b = 1 हैं।

(ii) k के किस मान के लिए निम्न रैखिक समीकरणों के युग्म का कोई हल नहीं है?
3x + y = 1
(2k – 1)x + (k – 1)y = 2k + 1
हल-
दिया गया रैखिक समीकरण युग्म है :
3x + y = 1
और (2k – 1)x + (k – 1)y = 2k + 1
या 3x + y – 1 = 0
और (2k – 1)x + (k – 1)y – (2k + 1) = 0
यहाँ a₁ = 3, b₁ = 1, c₁ = -1,
a₂ = (2k – 1), b₂ = k – 1, c₂ = -(2k + 1)
∴ दी गई समीकरण निकाय का कोई हल नहीं है

अतः k = 2 मान के लिए निम्न रैखिक समीकरण का कोई हल नहीं है।

प्रश्न 3.
निम्न रैखिक समीकरणों के युग्म को प्रतिस्थापन एवं वज्रगुणन विधियों से हल कीजिये। किस विधि को आप अधिक उपयुक्त मानते हैं?
8x + 5y = 9
3x + 2y = 4
हल-
दिया गया रैखिक समीकरण युग्म है :
8x + 5y = 9 ……(1)
3x + 2y = 4 ……(2)
प्रतिस्थापन विधि द्वारा-
(2) से, 2y = 4 – 3x

अतः, x = -2 और y = 5
वज्रगुणन विधि द्वारा-
रैखिक समीकरण युग्म
8x + 5y – 9 = 0
और 3x + 2y – 4 = 0
यहाँ a₁ = 8, b₁ = 5, c₁ = -9
a₂ = 3, b₂ = 2, c₂ = -4

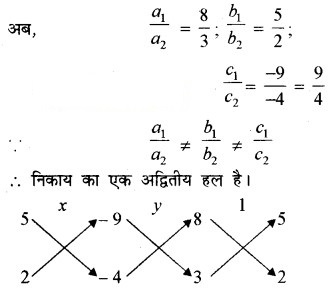
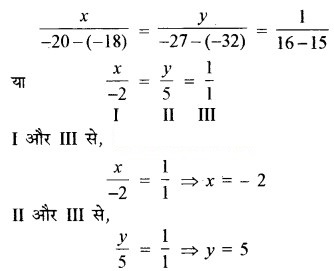
अतः दिये गये रैखिक समीकरण युग्म के हल x = -2 तथा y = 5 होंगे।

प्रश्न 4.
निम्न समस्याओं में रैखिक समीकरणों के युग्म बनाइए और उनके हल (यदि उनका अस्तित्व हो) किसी बीजगणितीय विधि से ज्ञात कीजिए-
(i) एक छात्रावास के मासिक व्यय का एक भाग नियत है तथा शेष इस पर निर्भर करता है कि छात्र ने कितने दिन भोजन लिया है। जब एक विद्यार्थी A को, जो 20 दिन भोजन करता है, 1000 रु. छात्रावास के व्यय के लिए अदा करने पड़ते हैं, जबकि एक विद्यार्थी B को, जो 26 दिन भोजन करता है, छात्रावास के व्यय के लिए 1180 रु. अदा करने पड़ते हैं। नियत व्यय और प्रतिदिन के भोजन का मूल्य ज्ञात कीजिए।
हल-
माना कि होस्टल का नियत मासिक किराया = x रु.
और प्रतिदिन भोजन का मूल्य = y रु.
पहली शर्त के अनुसार,
x + 20y = 1000 ……..(1)
प्रश्न की दूसरी शर्त के अनुसार,
x + 26y = 1180 …….(2)

अतः होस्टल का मासिक नियत किराया और प्रतिदिन भोजन का मूल्य क्रमशः 400 रु. और 30 रु. है।

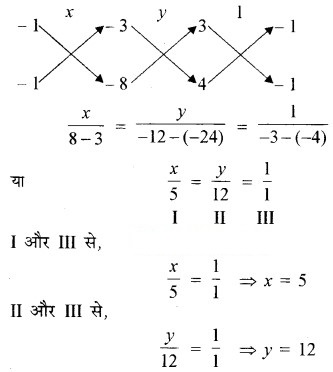
अतः, अभीष्ट भिन्न 5/12 है।

(iii) यश ने एक टेस्ट में 40 अंक अर्जित किए, जब उसे प्रत्येक सही उत्तर पर 3 अंक मिले तथा अशुद्ध उत्तर पर 1 अंक की कटौती की गई। यदि उसे सही उत्तर पर 4 अंक मिलते हैं तथा अशुद्ध उत्तर पर 2 अंक कटते, तो यश 50 अंक अर्जित करता। टेस्ट में कितने प्रश्न थे?
हल-
माना कि यश द्वारा किए गए सही प्रश्नों की संख्या = x
और यश द्वारा किए गए गलत प्रश्नों की संख्या = y
पहली शर्त के अनुसार,
3x – y = 40
या 3x – y – 40 = 0 ……(1)
दूसरी शर्त के अनुसार,
4x – 2y = 50
या 4x – 2y – 50 = 0 ……(2)
तब वज्रगुणन विधि से हल करने पर

∴ सही प्रश्नों की संख्या = 15
गलत प्रश्नों की संख्या = 5
अतः प्रश्नों की कुल संख्या = सही प्रश्नों की संख्या + गलत प्रश्नों की संख्या
= 15 + 5
= 20

(iv) एक राजमार्ग पर दो स्थान A और B, 100 km. की दूरी पर हैं। एक कार A से तथा दूसरी कार B से एक ही समय चलना प्रारम्भ करती है। यदि ये कारें भिन्न-भिन्न चालों से एक ही दिशा में चलती हैं, तो वे 5 घण्टे पश्चात् मिलती हैं। दोनों कारों की चाल ज्ञात कीजिए।
हल-
माना कि स्थान A वाली कार की चाल = x km/ hour
और स्थान B वाली कार की चाल = y km/hour
A और B के बीच की दूरी = 100 km
5 घण्टे की स्थिति में
कार A द्वारा तय की गई दूरी = 5x km [∵ दूरी = चाल × समय]
कार B द्वारा तय की गई दूरी = 5y km
पहली शर्त के अनुसार,
5x – 5y = 100
या x – y = 20 (∵ एक ही दिशा में है)
या x – y – 20 = 0 ………(1)
एक घण्टे की स्थिति में
कार A द्वारा तय की गई दूरी = x km [∵ दूरी = चाल × समय]
कार B द्वारा तय की गई दूरी = y km
दूसरी शर्त के अनुसार,
x + y = 100
या x + y – 100 = 0 ……(2)

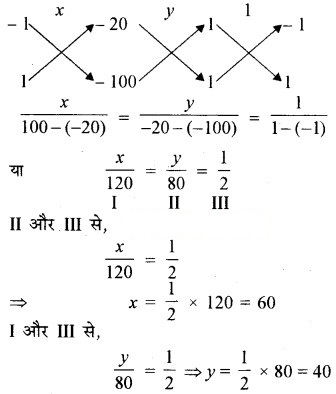
अतः, बिन्दुओं A तथा B से चलने वाली कारों की चालें क्रमशः 60 किमी./घण्टा और 40 किमी/घण्टा है।

(v) एक आयत का क्षेत्रफल 9 वर्ग इकाई कम हो जाता है, यदि उसकी लम्बाई 5 इकाई कम कर दी जाती है और चौड़ाई 3 इकाई बढ़ा दी जाती है। यदि हम लम्बाई को 3 इकाई और चौड़ाई को 2 इकाई बढ़ा दें, तो क्षेत्रफल 67 वर्ग इकाई बढ़ जाता है। आयत की विमाएँ ज्ञात कीजिए।
हल-
माना कि आयत की लम्बाई = x मात्रक
और आयत की चौड़ाई = y मात्रक
∴ आयत का क्षेत्रफल = xy sq. मात्रक
पहली शर्त के अनुसार,
(x – 5) (y + 3) = xy – 9
या xy + 3x – 5y – 15 = xy – 9
या 3x – 5y – 6 = 0 ……(1)
दूसरी शर्त के अनुसार,
(x + 3) (y + 2) = xy + 67
या xy + 2x + 3y + 6 = xy + 67
या 2x + 3y – 61 = 0 ……(2)

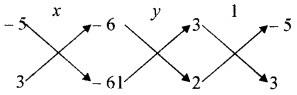
अत: आयत की लम्बाई और चौड़ाई क्रमशः 17 मात्रक और 9 मात्रक है।