Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
Question 1.
Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) 10 students of class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost ₹ 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Solution:
(i) Let the number of girls be x and number of boys be y.
A.T.Q.
1st Condition :
x +y =10
Table :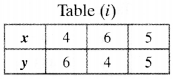
2nd Condition :
x = y + 4 ⇒ x – y = 4
Table :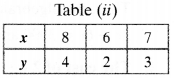
Solving
(i) and
(ii) graphically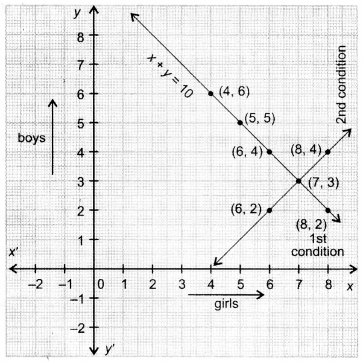
Both the lines cut at (7, 3)
Hence, solutions is (7, 3), i.e.x = 7,y = 3
Number of girls – 7 and Number of boys = 3
(ii) Let cost of 1 pencil = ₹ x and cost of 1 pen = ₹ y.
A.T.Q.
1st Condition :
5x + 7y = 50
Table :
2nd Condition :
7x + 5y = 46
Table :

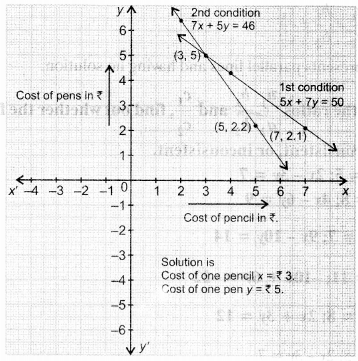
Question 2.
On comparing the ratios and find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5x – 4y + 8 = 7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0, 18x + 6y + 24 = 0
(iii) 6 – 3y + 10 = 0, Zx – v + 9 = 0
Solution:
(i) Equations are 5x – 4y + 8 = 7x + 6y – 9 = 0
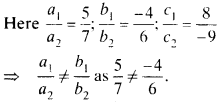
∴ Pair of lines represented by given equations intersect at one point. So, the system has exactly one solution.
(ii) 9x + 3y + 12 = 0, 18 + 6y + 24 = 0
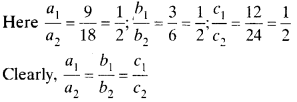
∴ Pair of equations represents coincident lines and having infinitely many solutions.
(iii) 6x – 3y + 10 = 0, 2x -y + 9 = 0
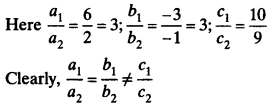
∴ It represents parallel lines and having no solution.
Question 3.
On comparing the ratios and find out whether the following pair of linear equations are consistent, or inconsistent,
(i) 3x + 2y = 5; 2x – 3y = 7
(ii) 2x – 3y = 8; 4x – 6y = 9
(iii) 3/2x + 5/3y = 7; 9x – 10y = 14
(iv) 5x-3y = 11; -10c + 6y = -22
(v) 4/3x + 2y = 8; 2x + 3y = 12
Solution:

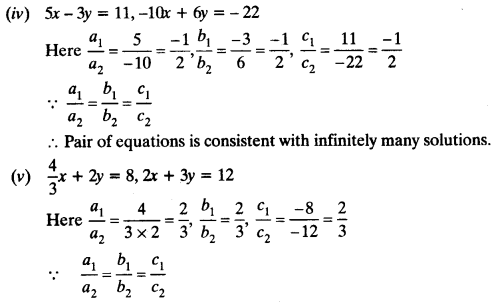
∴ Pair of equations is consistent with infinitely many solutions.
Question 4.
Which of the following pairs of linear equations are consistent/inconsistent If consistent, obtain the solution graphically:
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Solution:
(i) x + y – 5, 2x + 2y = 10
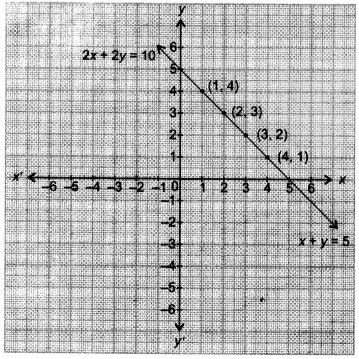
Here,
∴ System of equations is consistent and the graph gr represents coincident lines.
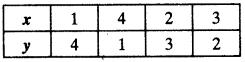
Table for equation (i),
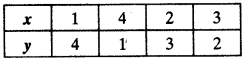
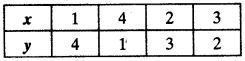
Table for equation (ii),
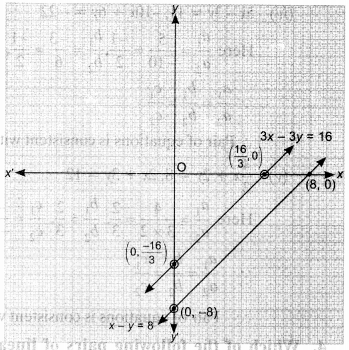
(ii) x – y = 8, 3x – 3y = 16
Here a1a2=13,
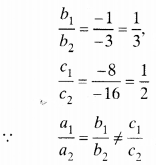
Pair of equations is inconsistent. Hence, lines are parallel and
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
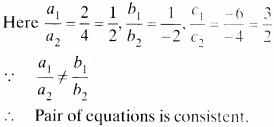
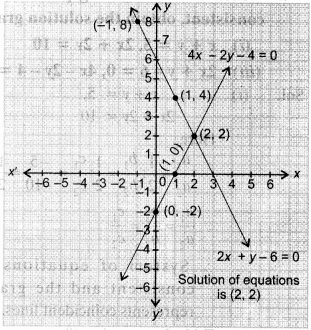
Pair of equations is consistent.
Table for equation 2x + y – 6 = ()
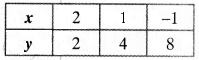
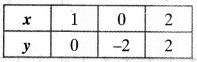
Table for equation 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
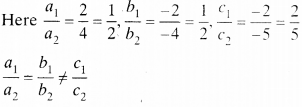
∴ Pair of equations is inconsistent. Hence, lines are parallel and system has no solution.
Question 5.
Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Solution:
Let length of garden = x m and width of garden = y m
Perimeter of rectangular garden = 2(x + y)

Question 6.
Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables, such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Solution:
Given equation is 2x + 3y – 8 – 0
We have 2x + 3y = 8
Let required equation be ax + by = c
Condition :
(i) For intersecting lines
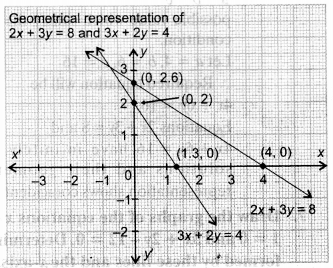

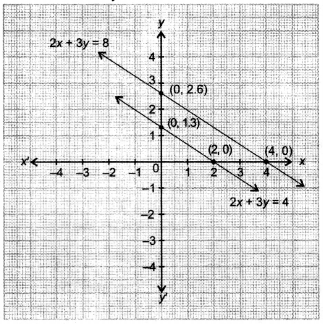
Equations 2x + 3y = 8 and 2x + 3y = 4 have no solution and their geometrical representation shows parallel lines.
(iii) For coincident lines:
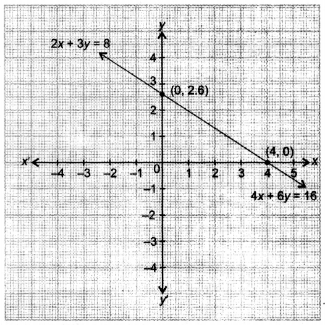

Question 7.
Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y -12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x – axis, and shade the triangular region.
Solution:
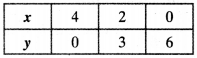
First equation is x – y + 1 = 0.
Table for 1st equation x = y – 1
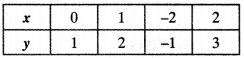
Second equation is 3x + 2y = 12
![]()
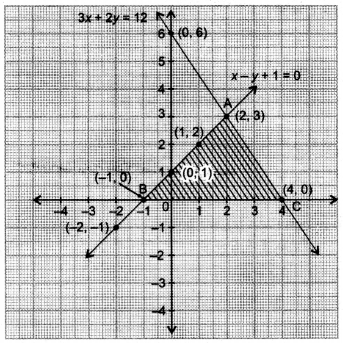
Required triangle is ABC. Coordinates of its vertices are A(2, 3), B(-1, 0), C(4, 0).