Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
Question 1.
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method.
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0
(ii) 2x + y = 5
3x + 2y = 8
(iii) 3x – Sy = 20
6x – 10y = 40
(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0
Solution:

(iii) Equations are 3x – 5y = 20 and 6x – 10y = 40
Here,
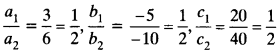

(iv) Equations are x – 3y = 7 and 3x – 3y = 15

Question 2.
(i) for which values of a and b does the following pai of linea equation have an infinite number of solutions₹
2x + 3y =7
(a – b)x + (a + b)y = 3a + b – 2
(ii) For which value of K will the following pair of linear equation have no solution₹
3x + y = 1
(2k – 1)x + (k – 1)y = 2k + 1
Solution:
(i) Equations are
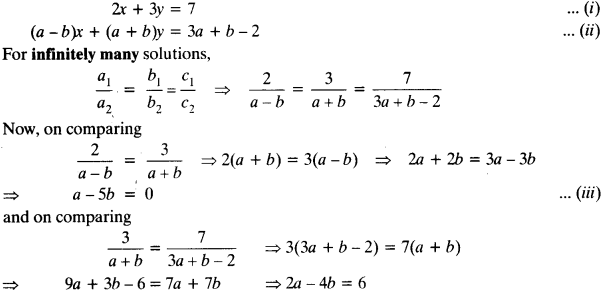
⇒ a – 2b = 3 Solving (iii) and (iv) for a and b
By cross multiplication method.

Question 3.
Solve the following pair of linear equations by the substitution and cross-multiplication methods:
8x + 5y = 9
3x + 2y = 4
Solution:
Equations are

By coss multiplication Method :
Equations are
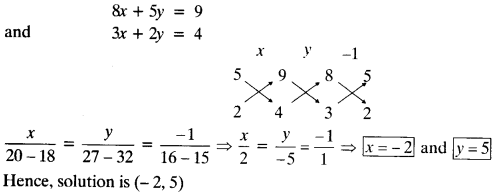
Question 4.
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method:
(i) A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay ₹ 1000 as hostel charges whereas a student B, who takes food for 26 days, pays ₹ 1180 as hostel charges. Find the fixed charges and the cost of food per day.
(ii) A fraction becomes 1/3 when 1 is subtracted from the numerator and it becomes 1/4 when 8 is added to its denominator. Find the fraction.
(iii) Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test₹
(iv) Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars ₹
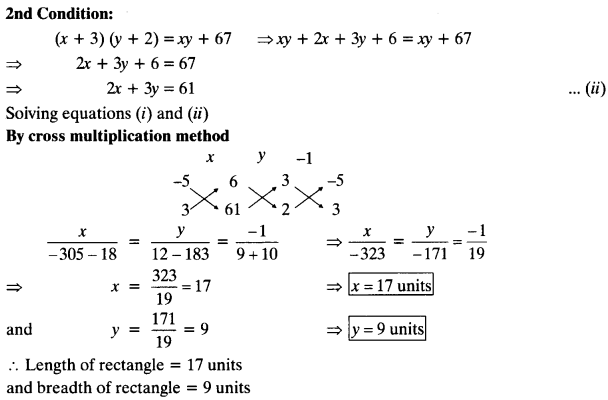
(v) The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.
Solution:
(i) Let fixed monthly hostel charges = and charges per day = ₹ y
A.T.Q.
As per condition of student A
x + 20y = 1000
As per condition of student B
x + 26y = 1180
By cross multiplication method
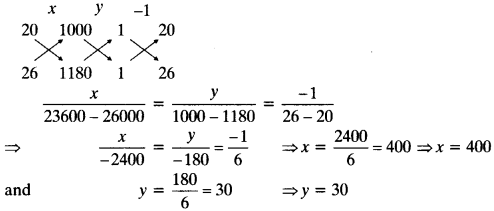
∴ Fixed monthly hostel charges = ₹ 400 and charges per day = ₹ 30
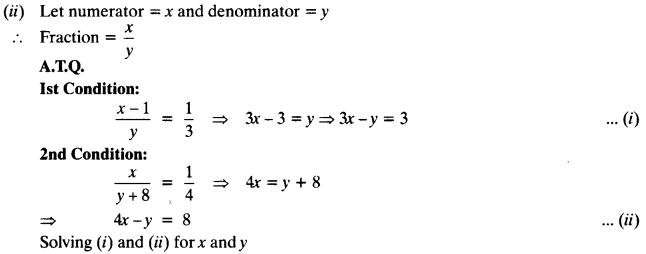
By cross multiplication method
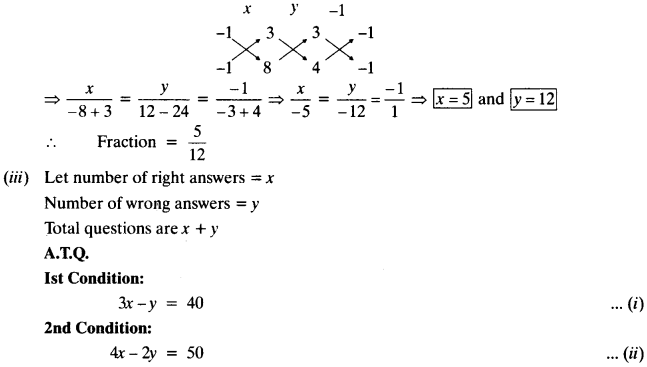
Solving (i) and (ii) for x and y
By cross multiplication method

By cross multiplication method