Chapter 4 सरल समीकरण Ex 4.3
प्रश्न 1.
निम्नलिखित समीकरणों को हल कीजिए :
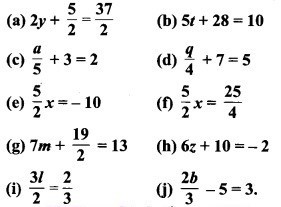
हल:

∴ अतः अभीष्ट हल :y = 8
(b) 5t + 28 = 10
या 5t = 10 – 28
या 5t = – 18
या t =
∴ अतः अभीष्ट हल : t =
(c) + 3 = 2
या = 2 – 3
या = -1
या a = -5
∴ अतः अभीष्ट हल : a = -5
(d) + 7 = 5 या
या = 5 – 7 = – 2
q = – 2 x 4 = -8
∴ अतः अभीष्ट हल : q = -8
(e) = – 10
दोनों पक्षों में 2 का गुणा करने पर,
x x 2 = – 10 x 2
या 5x = – 20
या =
या x = -4
∴ अभीष्ट हल : x = -4

(h) 6z + 10 = – 2
या 6z = -2 – 10 = – 12
या = -12 x
या = -2
∴ अभीष्ट हल : z = -2

प्रश्न 2.
निम्नलिखित समीकरणों को हल कीजिए :
(a) 2 (x + 4) = 12
(b) 3 (n – 5) = 21
(c) 3 (n – 5) = -21
(d) -4(2 + x) = 8
(e) 4(2 – x) = 8
हल:
(a) 2 (x + 4) = 12
या x + 4 = = 6 (दोनों पक्षों को 2 से भाग देने पर)
या x = 6 – 4 = 2 (4 को R.H.S. में स्थानापन्न करने पर)
∴ अभीष्ट हल : x = 2
(b) 3 (n – 5) = 21
या n – 5 = = 7 (दोनों पक्षों को 3 से भाग देने पर)
n = 7 + 5 = 12 (-5 को R.H.S. में स्थानापन्न करने पर)
∴ अभीष्ट हल : n = 12
(c) 3 (n – 5) = – 21
या n – 5 = = -7 (दोनों पक्षों को 3 से भाग देने पर)
या n = -7 + 5 = -2 (-5 को R.H.S. में स्थानापन्न करने पर)
∴ अभीष्ट हल : n = -2
(d) -4 (2 + x) = 8
या 2 + x = = -2. (दोनों पक्षों को -4 से भाग देने पर)
x = – 2 – 2 = -4 (2 को R.H.S. में स्थानापन्न करने पर)
∴ अभीष्ट हल : x = -4
(e) 4(2 – x) = 8
या 2 – x = =2 (दोनों पक्षों को 4 से भाग देने पर)
या -x = 2 – 2 = 0 (2 को R.H.S. में स्थानापन्न करने पर)
∴ x = 0
∴ अभीष्ट हल : x = 0
प्रश्न 3.
निम्नलिखित समीकरणों को हल कीजिए :
(a) 4 = 5 (p – 2)
(b) -4 = 5 (p – 2)
(c) 16 = 4 + 3 (t + 2)
(d) 4 + 5 (p – 1) = 34
(e) 0 = 16 + 4 (m – 6).
हल:
(a) 4 = 5 (p – 2)
या 5 (p – 2) = 4 (दोनों पक्षों को परस्पर बदलने पर)
या p – 2 = 4 (दोनों पक्षों को 5 से भाग देने पर)
या p = + 2 (-2 को R.H.S. में स्थानापन्न करने पर)
p = =
∴ अभीष्ट हल : p =
(b) – 4 = 5 (p – 2)
या 5 (p – 2) = -4 (दोनों पक्षों को परस्पर बदलने पर)
या p – 2 = (दोनों पक्षों को 5 से भाग देने पर)
या p = + 2 (-2 को R.H.S. में स्थानापन्न करने पर)
या p = =
∴ अभीष्ट हल : p = 6/5
(c) 16 = 4+ 3 (t + 2)
4 + 3 (t + 2) = 16 (दोनों पक्षों को परस्पर बदलने पर)
या 3 (t + 2) = 16 – 4 = 12 (4 को R.H.S. में स्थानापन्न करने पर)
या t + 2 = 12/3 = 4 (दोनों पक्षों को 3 से भाग देने पर)
या t = 4 – 2 = 2 (2 को R.H.S. में स्थानापन्न करने पर)
∴ अभीष्ट हल : t = 2
(d) 4 + 5 (p – 1) = 34
या 5 (p – 1) = 34 – 4 = 30 (4 को R.H.S. में स्थानापन्न करने पर)
या (p – 1) = 30/5 = 6 (दोनों पक्षों को 5 से भाग देने पर)
p = 6 + 1 = 7 (-1 को R.H.S. में स्थानापन्न करने पर)
∴ अभीष्ट हल : p = 7
(e) 0 = 16 + 4 (m – 6)
या 16 + 4 (m – 6)= 0 (दोनों पक्षों को परस्पर बदलने पर)
या 4 (m – 6) = 0 -16 (16 को R.H.S. में ले जाने पर)
या m – 6 = = – 4 (दोनों पक्षों को 4 से भाग देने पर)
या m = -4 + 6 = 2 (-6 को R.H.S. में स्थानापन्न करने पर)
∴ अभीष्ट हल : m = 2
प्रश्न 4.
(a) x = 2 से प्रारम्भ करते हुए, 3 समीकरण बनाइए।
(b) x =-2 से प्रारम्भ करते हुए, 3 समीकरण बनाइए।
हल:
(a) (i) प्रथम समीकरण : x = 2 से शुरू दोनों पक्षों को 5 से गुणा करने पर,
5x = 10
दोनों ओर से 3 घटाने पर,
5x – 3 = 10 – 3
या 5x – 3 = 7
(ii) द्वितीय समीकरण : x = 2 से शुरू
दोनों पक्षों को 10 से गुणा करने पर,
10x = 2 x 10 = 20
दोनों पक्षों में 2 जोड़ने पर,
10 + 2 = 20 + 2
या 10x + 2 = 22

(b) (i) प्रथम समीकरण : x = – 2 से प्रारम्भ
दोनों पक्षों को 3 से गुणा करने पर,
या 3x = – 6
दोनों पक्षों में से 2 घटाने पर,
3x – 2 = – 6 – 2
या 3x – 2 = -8
(ii) द्वितीय समीकरण : x = – 2 से प्रारम्भ
दोनों पक्षों को 3 से गुणा करने पर,
3x = – 6
दोनों पक्षों में 7 जोड़ने पर,
3x + 7 = -6 + 7
या 3x + 7 = 1
(iii) तृतीय समीकरण : x = – 2 से प्रारम्भ
दोनों पक्षों को 8 से गुणा करने पर,
8x = – 16
दोनों पक्षों में 10 जोड़ने पर,
8x + 10 = – 16 + 10
⇒ 8x +10 = – 6
पाठ्य-पुस्तक पृष्ठ संख्या # 101
प्रयास कीजिए
प्रश्न (i)
जब आप एक संख्या को 6 से गुणा करते हैं और फिर गुणनफल में से 5 घटाते हैं, तो आपको 7 प्राप्त होता है। क्या आप बता सकते हैं कि वह संख्या क्या है ?
हल:
माना कि संख्या x है।
संख्या को 6 से गुणा करने पर, हम पाते हैं 6x
अब, प्रश्नानुसार,
6x – 5 = 7
5 को L.H.S. से R.H.S. में स्थानापन्न करने पर, हम प्राप्त करते हैं :
6x = 7 + 5 = 12
दोनों पक्षों को 6 से भाग देने पर,
x = = अथवा x = 2
अतः अभीष्ट संख्या : 2.
प्रश्न (ii)
वह कौन-सी सख्या है, जिसके एक-तिहाई में 5 जोड़ने पर 8 प्राप्त होता है ?
हल:

प्रयास कीजिए
प्रश्न 1.
मापों के अनुसार, दो प्रकार की पेटियाँ हैं, जिनमें आम रखे हुए हैं। प्रत्येक बड़ी पेटी में रखे आमों की संख्या 8 छोटी पेटी में रखे आमों की सख्या से 4 अधिक है। प्रत्येक बड़ी पेटी में 100 आम हैं। प्रत्येक छोटी पेटी में कितने आम हैं ?
हल:
माना कि छोटी पेटी में आमों की संख्या = x है।
∴ 8 छोटी पेटियों में आमों की संख्या = 8x
अब, प्रश्नानुसार,
8x + 4 = 100
4 को R.H.S. में स्थानापन्न करने पर,
8x = 100 – 4
अथवा 8x = 96
दोनों पक्षों में 8 से भाग देने पर,
अथवा x = 12
अतः छोटी पेटी में आमों की संख्या = 12