Chapter 4 Moving Charges and Magnetism
Question 1.
A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the center of the coil?
Answer:

Question 2.
A long straight wire carries a current of 35 A. What is the magnitude of the Held B at a point 20 cm from the wire ?
Answer:
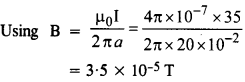
Question 3.
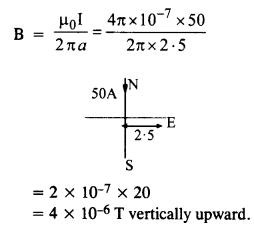
A long straight wire in the horizontal plane carries a current of 50 A in the north to south direction. Give the magnitude and direction of R at a point 2.5 m east at the wire.
Answer:
Question 4.
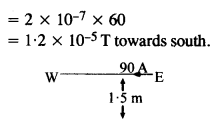
A horizontal overhead power line carries a current of 90A in the east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?
Answer: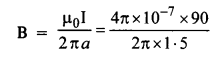
Question 5.
What is the magnitude of magnetic force per unit length on a wire carrying a current of 8 A and making an angle of 30° with the direction of a uniform magnetic field of 0.15 T?
Answer:
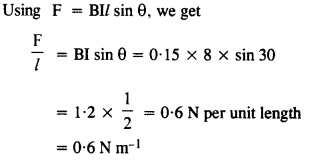
Question 6.
A 3.0 cm wire carrying a current of 10A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?
Answer:
I = 10 A, B = 0.27 T
1 = 3cm = 0.3m
and θ = 90°
F = BI 1 sin θ
=0.27×10 × 0.03 × sin90°
= 0.27×10 x 0.03 x 1
= 8.1 × 10-2N.
Question 7.
Two long and parallel straight wires A and B carrying currents of 8*0 A and 5*0 A in the same direction are separated by a distance of 4-0 cm. Estimate the force on a 10 cm section of wire A.
Answer:
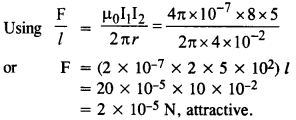
Question 8.
A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its center.
Answer:

Question 9.
A square coil of side 10 cm consists for 20 turns and carries a current of 12 A. The coil is suspended vertically and the normal to the plane of the coil makes an angle of 30° with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil?
Answer:
N = 20, A = 100 x 10-4 m2
I = 12 A
B = 0.8 T
θ = 30°
Torque, τ = NI(A¯ x B¯)
= 20 x 12 x 100 x 10-4 x 0.8 x sin 30°1
= 20 x 12 x 100 x 10-4 x 0.8 x 12
= 0.96 Nm
Question 10.
Two moving .coil meters, M1and M2 has the following particulars:
R1 = 10 Ω, N1 = 30, A1= 3.6 x 10-3m2, B1= 0.25 T
R2 = 14 Ω, N2 = 42, A2 = 1.8 x 10-3 m2, B2 = 0.50 T (The spring constants are identical for the two meters). Determine the ratio of (a) current sensitivity and (b) voltage sensitivity of M2 and M1.
Answer:
Using Current sensitivity = NBA/k
For M1 Current Sensitivity

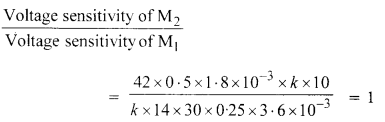
Question 11.
In a chamber, a uniform magnetic field of 6.5G (1G = RHT) is maintained. An electron is shot into the field with a speed of 4.8 x 106 ms-1 normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circular orbit,
(e =1.6 x 10-19 C, m = 9.1 x 10-31 kg).
Answer:
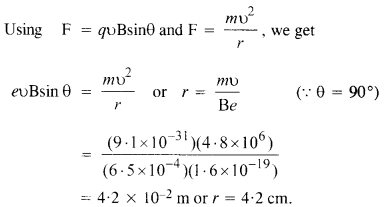
Question 12.
In Exercise 4.11 obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain.
Answer:

Question 13.
(a) A circular coil of 30 turns and radius 8-0 cm carrying a current of 6-0 A is suspended vertically in a uniform horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of 60° with the normal of the coil. Calculate the magnitude of the counter-torque that must be applied to prevent the coil from turning.
(b) Would your answer change, if the circular coil in (a) were replaced by a planar toil of some irregular shape that encloses the same area? (All other particulars are also unaltered) (C.B.S.E. 1998 C )
Answer:
(a) Using τ = NBIA sin 9, we get
τ= 30 X 1 x 6 x n (8 X 10-2)2 sin 60
= 180 x it (8 x 10-2)2 0.866
= 3.13 N m
The magnitude of the counter-torque is 3 .13 N m
(b) Answer will not change because torque does not depend upon the shape of the coil provided it encloses the same area.
Question 14.
Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A: coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their center.
Answer:
For Coil X

Question 15.
A magnetic field of 100 G (1 G = 10-4 T) is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about 10-3 m2. The maximum current-carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a core is at most 1000 turns m-1. Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic.
Answer:
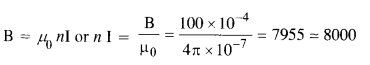
We may take I = 10 A and n = 800. The given solenoid may have a length of 50 cm having 400 turns and area of cross-section = 5 x 10-3m2 (five times the given value.)
Question 16.
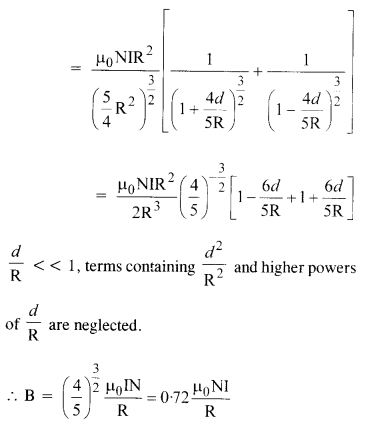
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its center is given by,
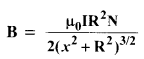
(a) Show that this reduces to the familiar result for field at the center of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by,
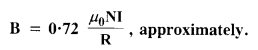
(Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.)
Answer:

(b) Let there be two coils as mentioned in the statement. The magnetic field in a small region of length 2d about the mid-point of the space between the two coils is given by,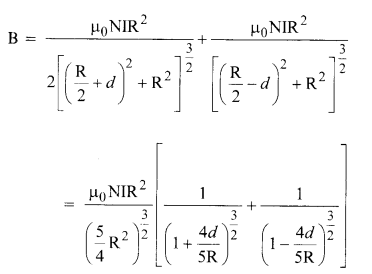
Question 17.
A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field
(i) outside the toroid
(ii) inside the core of the toroid, and
(iii) in the empty space surrounded by the toroid?
Answer:
(i) Zero
Question 18.
Answer the following questions:
(a) A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?
(b) A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?
(c) An electron travelling west to east enters a chamber having a uniform electrostatic field in the north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight-line path.
Answer:
(a) The force on a charged particle moving inside the magnetic field is given by
F⃗ m=q(v⃗ ×B⃗ )
The force on the charged particle coil bd zero (will remain undeflected), if v x B is zero. Therefore, either the initial velocity v is parallel or anti-parallel to the magnetic field B.
(b) The magnetic field exerts force on the charged particle, which is always perpendicular to its motion and hence does no work. Therefore, charged particle will have its final speed equal to its initial speed, provided it suffered no collision with the environment.
(c) Under the action of the electrostatic field, the electron will be deflected towards north (towards the positive plate). It will remain undeflected if the force due to the magnetic field is towards south. As the velocity: y of the electron is from west to east, the expression for the magnetic Lorentz force i.e. F⃗ m=−e(v⃗ ×B⃗ ) it tells that the magnetic field B⃗ should be applied along the vertical and in downward direction. The direction of the magnetic field may be found by applying Fleming’s left-hand rule.
Question 19.
An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field (a) is transverse to its initial velocity, (b) makes an angle of 30° with the initial velocity.
Answer:
K.E, acquired by electron while passing through V

(b) When electron moves with velocity r making an angle of 30° with the direction of magnetic field, then r cos θ is

Question 20.
A magnetic field set up using Helmholtz coils (described in Exercise 4.16) is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is 9.0 x 105 V m-1, make a simple guess as to what the beam contains. Why is the answer not unique.
Answer:
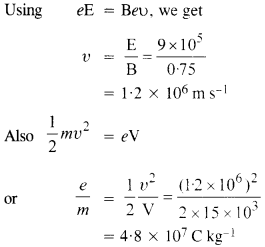
The given particle may be deutron.
The result is not unique because this e/m ratio can be true for He+ + , Li + + + etc.
Question 21.
A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.”
(a) What magnetic field should be set up normally to the conductor in order that the tension in the wires is zero?
(b) What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field the same as before? (Ignore the mass of the wires.) g = 9.8 ms-2.
Answer:
(a) The tension in the wire is zero if the force on the current-carrying wire due to current is equal and opposite to the weight of the wire. This is, BIl= mg
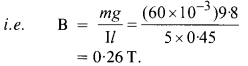
(b) In case the current is reversed, the tension is equal to the force acting on the wire due to the magnetic field plus the weight of the wire. This is,
T = BlL + mg
= 0.26 x 5 x 0.45 + 60 x 10-3 x 9.8
= 1.18 N.
Question 22.
The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive (H.S.E.B.2001)
Answer:

Since the currents in two wires are in opposite directions so the force is repulsive.
Question 23.
A uniform magnetic field of 1.5 T exists in a cylindrical region of a radius 10.0 cm, its direction parallel to the axis along east to west. A wire carrying a current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,
(a) the wire intersects the axis,
(b) the wire is turned from N-S to the northeast-northwest direction?
(c) the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?
Answer:


Question 24.
A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Figure? What is the force on each case? Which case corresponds to stable equilibrium?

Answer:


Question 25.
A circular coil of 20 turns and a radius of 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) the total force on the coil,
(c) average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10-5 m2, and the free electron density in copper is given to be about 1029 m3)
Answer:

Question 26.
A solenoid 60 cm long and of radius 4.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its center) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with an appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? g = 9.8 ms-2.
Answer:

Question 27.
A galvanometer coil has a resistance of 12 Q and the meter shows full-scale deflection for a current of 3 mA. How will you convert the meter into a voltmeter of range 0 to 18 V?
Answer:
Here 1=3 mA = 3 x 10-3 A
Galvanometer resistance, G = 12 Ω The galvanometer can be converted into the voltmeter of range 0 to V (here V = 18 V) by connecting a high series resistance R given

Question 28.
A galvanometer coil has a resistance of 15Ω and the meter shows full-scale deflection for a current of 4 mA. How will you convert the meter into an ammeter of range 0 to 6?
Answer:
