Chapter 6 त्रिभुज Ex 6.3
प्रश्न 1.
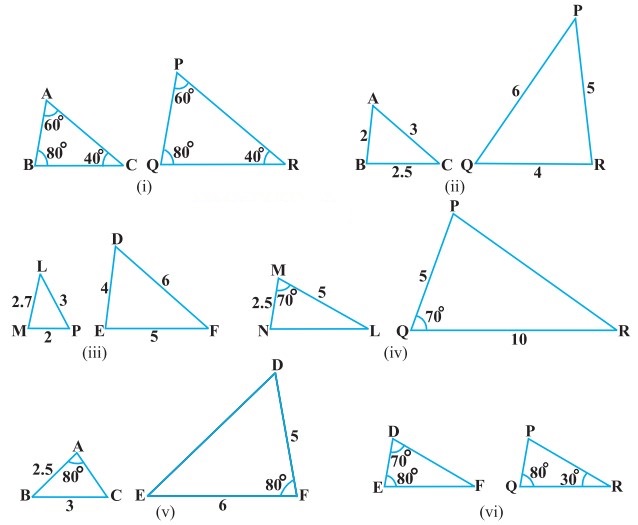
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौनसे युग्म समरूप हैं। उस समरूपता की कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
हल-
(i) ΔABC तथा ΔPQR में,
∠A = ∠P (प्रत्येक 60°)
∠B = ∠Q (प्रत्येक 80°)
∠C = ∠R (प्रत्येक 40°)
∴ ΔABC ~ ΔPQR
अर्थात् दोनों Δ समरूप हैं। [AAA समरूपता कसौटी]


(vi) ΔDEF में,
∠D = 70°, ∠E = 80°
∵ ∠D + ∠E + ∠F = 180°
या 70° + 80° + ∠F = 180°
या ∠F = 180° – 70° – 80°
या ∠F = 30°
ΔPQR में,
∠Q = 80°, ∠R = 30°
∵ ∠P + ∠Q + ∠R = 180°
या ∠P + 80° + 30° = 180°
या ∠P = 180° – 80° – 30°
अतः ∠P = 70°
ΔDEF तथा ΔPQR में,
∠D = ∠P (प्रत्येक कोण 70°)
∠E = ∠Q (प्रत्येक कोण 80°)
∠F = ∠R (प्रत्येक कोण 30°)
∴ ΔDEF ~ ΔPQR (AAA समरूपता कसौटी)
अर्थात् दोनों त्रिभुज समरूप हैं।
प्रश्न 2.
आकृति में, ΔODC ~ ΔOBA, ∠BOC = 125° और ∠CDO = 70° है। ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए।

हल-
∠BOC = 1250
∠CDO = 70°
DOB एक सरल रेखा है।
∴ ∠DOC + ∠COB = 180°
या ∠DOC + 125° = 180°
या ∠DOC = 180° – 125°
या ∠DOC = 55°
∠DOC = ∠AOB = 55° [शीर्षाभिमुख कोण]
∴ ΔODC ~ ΔOBA
∠D = ∠B = 70°
ΔDOC में,
∠D + ∠O + ∠C = 180°
70° + 55° + ∠C = 180°
∠C = 180° – 70° – 55°
∠C = 55°
∠C = ∠A = 55°
∴ ∠DOC = 55°
∠DCO = 55°
∠OAB = 55°
प्रश्न 3.
समलम्ब ABCD, जिसमें AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं। दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए, दर्शाइए कि

हल-
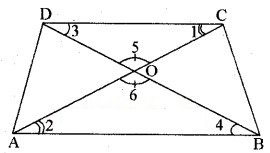


हल-

प्रश्न 5.
ΔPQR की भुजाओं PR और QR पर क्रमशः बिन्दु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है। दर्शाइए कि ΔRPQ ~ ΔRTS है।
हल-
दिया है : ΔPQR की भुजाओं PR और OR पर क्रमशः बिन्दु S और T इस प्रकार स्थित हैं कि ∠P = ∠RTS है।

सिद्ध करना है : ΔRPQ ~ ΔRTS
उपपत्ति : ΔRPQ और ΔRTS में,
∠RPQ = ∠RTS (दिया है)
∠PRQ = ∠TRS (उभयनिष्ठ कोण)
![]()
SAS समरूपता कसौटी से
ΔRPQ ~ ΔRTS (इतिसिद्धम्)
प्रश्न 6.
आकृति में, यदि ΔABE ≅ ΔACD है, तो दर्शाइए कि ΔADE ~ ΔABC है।

हल-
दिया है : ΔABE ≅ ΔACD है।
सिद्ध करना है : ΔADE ~ ΔABC
उपपत्ति : ΔABE ≅ ΔACD (दिया है)
AB = AC (सर्वांगसम त्रिभुजों के संगत भुजाएँ)
और AE = AD (सर्वांगसम त्रिभुजों के संगत भुजाएँ)

∠A = ∠A (उभयनिष्ठ कोण)
∴ ΔADE ~ ΔABC [SAS समरूपता कसौटी से]
प्रश्न 7.
आकृति में, ΔABC के शीर्षलम्ब AD और CE परस्पर बिन्दु P पर प्रतिच्छेद करते हैं। दर्शाइए कि:
(i) ΔAEP ~ ΔCDP
(ii) ΔABD ~ ΔCBE
(iii) ΔAEP ~ ΔADB
(iv) ΔPDC ~ ΔBEC

हल-
दिया है : ΔABC, AD ⊥ BC, CE ⊥ AB
सिद्ध करना है :
(i) ΔAEP ~ ΔCDP
(ii) ΔABD ~ ΔCBE
(iii) ΔAEP ~ ΔADB
(iv) ΔPDC ~ ΔBEC
उपपत्ति :
(i) ΔAEP और ΔCDP में,
∠E = ∠D (प्रत्येक 90°)
∠APE = ∠CPD (शीर्षाभिमुख कोण)
∴ ΔAEP ~ ΔCDP [AA समरूपता कसौटी]
(ii) ΔABD और ΔCBE में,
∠D = ∠E (प्रत्येक 90°)
∠B = ∠B (उभयनिष्ठ कोण)
∴ ΔABD ~ ΔCBE [AA समरूपता कसौटी]
(iii) ΔAEP और ΔADB में,
∠E = ∠D (प्रत्येक 90°)
∠A = ∠A (उभयनिष्ठ कोण)
∴ ΔAEP ~ ΔADB [AA समरूपता कसौटी]
(iv) ΔPDC और ΔBEC में,
∠C = ∠C (उभयनिष्ठ कोण)
∠D = ∠E (प्रत्येक 90°)
∴ ΔPDC ~ ΔBEC [AA समरूपता कसौटी]
प्रश्न 8.
समान्तर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिन्दु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ΔABE ~ ΔCFB है।
हल-
दिया है : समान्तर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिन्दु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है।
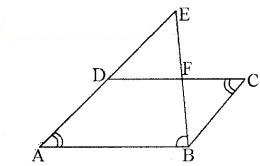
सिद्ध करना है : ΔABE ~ ΔCFB
उपपत्ति : ΔABE और ΔCFB में,
∠A = ∠C (समांतर चतुर्भुज के सम्मुख कोण)
∠ABE = ∠CFB (एकान्तर कोण)
∴ ΔABE ~ ΔCFB (AA समरूपता कसौटी)
(इतिसिद्धम्)
प्रश्न 9.
आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि
(i) ΔABC ~ ΔAMP
![]()

हल-
दिया है : ΔABC और ΔAMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं।
सिद्ध करना है :

प्रश्न 10.
CD और GH क्रमशः ∠ACB और ∠EGF के ऐसे. समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔFEG की भुजाओं AB और FE पर स्थित हैं। यदि ΔABC ~ ΔFEG हैं, तो दर्शाइए कि :
![]()
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGF
हल-

दिया है : ΔABC और ΔEFG में, CD और GH क्रमशः ∠ACB और ∠EGF के समद्विभाजक हैं अर्थात् ∠1 = ∠2 और ∠3 = ∠4 हैं तथा ΔABC ~ ΔFEG हैं।
सिद्ध करना है :
![]()
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGF
उपपत्ति : (i) ΔABC ~ ΔFEG (दिया है)
∠C = ∠G [यदि दो त्रिभुज समरूप हों, तो संगत कोण बराबर होते हैं।]
![]()
∠1 = ∠3 या ∠2 = ∠4
अथवा ∠1 = ∠4
∠2 = ∠3
अब, ΔACD और ΔFGH में,
∠A = ∠F (ΔABC ~ ΔFEG)
∠2 = ∠4 (सिद्ध कर चुके हैं।)
∴ ΔACD ~ ΔFGH [∵ AA समरूपता कसौटी से]
![]()
(ii) अब, ΔDCB और ΔHGE में,
∠B = ∠E (∵ ΔABC ~ ΔFEG)
∠1 = ∠4 (ऊपर सिद्ध कर चुके हैं।)
∴ ΔDCB ~ ΔHGE [∵ AA समरूपता कसौटी से]
(iii) अब, ΔDCA और ΔHGF में,
∠A = ∠F (∵ ΔABC ~ ΔFEG)
∠2 = ∠3 (सिद्ध कर चुके हैं।)
∴ ΔDCA ~ ΔHGF [∵ AA समरूपता कसौटी से]
(इतिसिद्धम्)
प्रश्न 11.
आकृति में, AB = AC वाले, एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिन्दु है। यदि AD ⊥ BC और EF ⊥ AC है, तो सिद्ध कीजिए कि ΔABD ~ ΔECF है।

हल-
दिया है : AB = AC वाले एक समद्विबाहु ΔABC की बढ़ाई गई भुजा CB पर स्थित E एक बिन्दु है।
AD ⊥ BC और EF ⊥ AC है।
सिद्ध करना है : ΔABD ~ ΔECF
उपपत्ति : ΔABC समद्विबाहु त्रिभुज है (दिया है)
AB = AC (क्योंकि त्रिभुज में समान भुजाओं के सम्मुख कोण बराबर होते हैं)
∴ ∠B = ∠C (समान कोण)
ΔABD और ΔECF में,
∠ABD = ∠ECF (सिद्ध कर चुके हैं)
∠ADB = ∠EFC (प्रत्येक 90°)
∴ ΔABD ~ ΔECF [AA समरूपता]
(इतिसिद्धम्)
प्रश्न 12.
एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ और QR तथा माध्यिका PM के समानुपाती हैं (देखिए आकृति)। दर्शाइए कि ΔABC ~ ΔPQR है।

हल-
दिया है : ΔABC की माध्यिका AD और ΔPQR की माध्यिका PM इस तरह से है कि

प्रश्न 13.
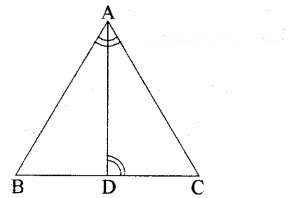
एक त्रिभुज ABC की भुजा BC पर बिन्दु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। दर्शाइए कि CA2 = CB . CD है।
हल-
दिया है : ΔABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ADC = ∠BAC
सिद्ध करना है : CA2 = BC . CD
उपपत्ति : ΔABC और ΔADC में,
∠C = ∠C (उभयनिष्ठ कोण)
∠BAC = ∠ADC (दिया है)
∴ ΔABC ~ ΔDAC [AA समरूपता कसौटी से]

प्रश्न 14.
एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं। दर्शाइए कि ΔABC ~ ΔPQR है।
हल-
दिया है : दो त्रिभुज ABC और PQR में D, BC का मध्य-बिन्दु है और M, QR का मध्य-बिन्दु है।
![]()

सिद्ध करना है : ΔABC ~ ΔPQR
रचना : AD को E तक बढ़ाइए ताकि AD = DE हो। BE और CE को मिलाइए।
PM को N तक बढ़ाइए ताकि PM = MN हो।
QN और NR को मिलाइए।
उपपत्ति : चतुर्भुज ABEC के विकर्ण AE और BC परस्पर D पर समद्विभाजित करते हैं। अत: चतुर्भुज ABEC एक समान्तर चतुर्भुज है।
इसी प्रकार यह दर्शाया जा सकता है कि चतुर्भुज PQNR एक समान्तर चतुर्भुज है।
चूंकि ABEC एक समान्तर चतुर्भुज है।
∴ BE = AC ……(ii)
इसी प्रकार चूँकि DQNR एक ||gm है।
∴ QN = PR …….(iii)
(ii) को (iii) से विभाजित करने पर

∴ ΔABC ~ ΔPON
∴ ∠BAE = ∠QPN …….(vi)
इसी प्रकार, यह सिद्ध किया जा सकता है कि
ΔAEC ~ ΔPNR
∴ ∠EAC = ∠NPR ……(vii)
अब (vi) और (vii) को जोड़ने पर
∠BAE + ∠EAC = ∠QPN + ∠NPR
अर्थात् ∠BAC = ∠QPR
![]()
∠A = ∠P
∴ ΔABC ~ ΔQPR [SAS समरूपता कसौटी से]
प्रश्न 15.
लम्बाई 6 m वाले एक ऊर्ध्वाधर स्तम्भ की भूमि पर छाया की लम्बाई 4 m है, जबकि उसी समय एक मीनार की छाया की लम्बाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
हल-
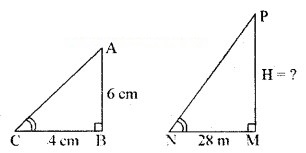
ऊर्ध्वाधर स्तम्भ की लम्बाई = 6 m
स्तम्भ की छाया की लम्बाई = 4 m
माना कि मीनार की ऊँचाई = H m
मीनार की छाया की लम्बाई = 28 m
ΔABC और ΔPMN में,
∠C = ∠N (मीनार की छाया की लम्बाई)
∠B = ∠M (प्रत्येक 90°)
∴ ΔABC ~ ΔPMN [AA समरूपता कसौटी]

⇒ H = 6 x 7
⇒ H = 42 m
अतः मीनार की ऊँचाई = 42 m
प्रश्न 16.

हल-
दिया है : ΔABC और ΔPQR की AD और PM माध्यिकाएँ हैं तथा ΔABC ~ ΔPQR है।