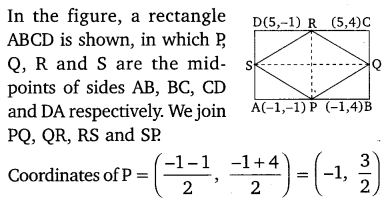Chapter 7 Coordinate Geometry Ex 7.4

Chapter 7 Coordinate Geometry Ex 7.4

Question 1.
Determine the ratio, in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, -2) and B(3, 7).
Solution:

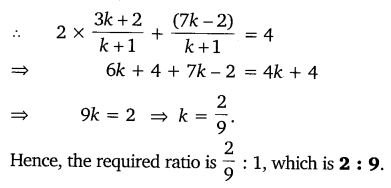
Question 2.
Find a relation between x and y, if the points (x, y), (1, 2) and (7, 0) are collinear.
Solution:

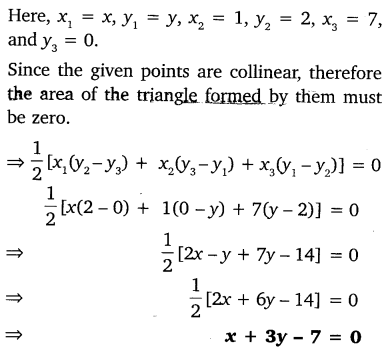
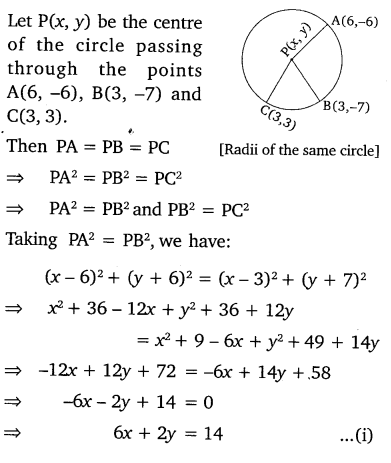
Question 3.
Find the centre of a circle passing through the points (6, -6), (3, -7) and (3, 3).
Solution:

Question 4.
The two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of the other two vertices.
Solution:

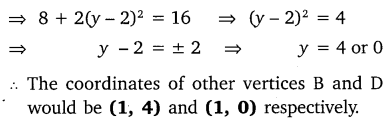
Question 5.
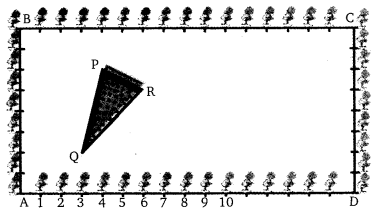
The class X students school in krishnagar have been alloted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m fron eaach other. There is trianguler grassy lawn in the plot as shoen in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.
(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of ∆PQR, if C is the origin?
Also, calculate the areas of the triangles in these cases. What do you observe?

Solution:

Question 6.

Solution:

Question 7.
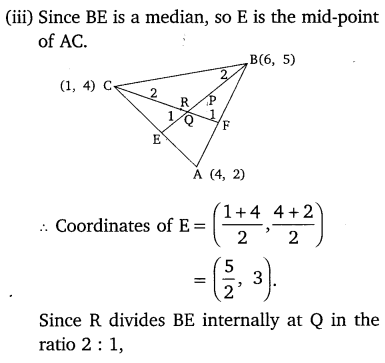
Let A(4, 2), B(6,5) and C(1, 4) be the vertices of ∆ABC.
(i) The median from A meters BC at D. Find the coordinates ofthe point D.
(ii) Find the coordinates of the point P on AD, such that AP : PD = 2 : 1.
(iii) Find the coordinates of points Q and R on medians BE and CF respectively, such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What do you observe?
[Note: The points which is common to all the three medians is called centroid and this point divides each median in the ratio 2 : 1]
(v) If A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are the vertices of ∆ABC, find the coordinates of the centroid of the triangles.
Solution:




Question 8.
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1), P, Q, R and S are the mid-points of Ab, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Solution: