Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.3
प्रश्न 1.
आकृति में, ∆ABC की एक माध्यिका AD पर स्थित E कोई बिन्दु है। दर्शाइए कि ar (ABE) = ar (ACE) है।

हल:
प्रश्नानुसार ∆ABC में माध्यिका AD है।
अतः ar (∆ABD) = ar (∆ACD) …..(i)
क्योंकि हम जानते हैं कि माध्यिका त्रिभुज को बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
पुनः ∆EBC में ED एक माध्यिका है।
अतः ar (∆EBD) = ar (∆ECD) …..(ii)
समीकरण ()i में से (ii) को घटाने पर ar (∆ABD) – ar (∆EBD) = ar (∆ACD) – ar (∆ECD)
या ar (∆ABE) = ar (∆ACE) ( इति सिद्धम् )
प्रश्न 2.
∆ABC में, E माध्यिका AD का मध्यबिन्दु है। दर्शाइए कि ar (BED) = 1/4ar (ABC) है।
हल:
दिया है-एक D ABC है जिसमें AD एक माध्यिका है और E माध्यिका AD का मध्य बिन्दु है।


प्रश्न 3.
दर्शाइए कि समान्तर चतुर्भुज के दोनों विकर्ण | उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाँटते हैं।
हल:
माना कि एक समान्तर चतुर्भुज ABCD है जिसके विकर्ण क्रमश: AC तथा BD एक-दूसरे को बिन्दु 0 पर प्रतिच्छेदित करते हैं । बने हुए ∆ABC तथा ∆ADC में

AB = DC (समान्तर चतुर्भुज की सम्मुख भुजाएँ)
BC = AD (समान्तर चतुर्भुज की सम्मुख भुजाएँ)
AC = AC (उभयनिष्ठ भुजाएँ)
अतः ∆ABC ≅ ∆CDA (सर्वांगसमता के नियम SSS के अनुसार)
चूँकि हम जानते हैं कि समान्तर चतर्भज के विकर्ण परस्पर समद्विभाजित होते हैं अतः चित्र में 0 समद्विभाजक बिन्दु होगा। अब A ADC में DO एक माध्यिका है। अतः
ar (∆AOD) = ar (∆COD) …..(i)
क्योंकि माध्यिका त्रिभुज को बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है। इसी प्रकार A ABC में OB एक माध्यिका है। अत:
ar (∆AOB) = ar (∆BOC) …..(ii)
∆AOB तथा ∆AOD में A एक माध्यिका है ।
अतः ar (∆AOB) = ar (∆AOD) …..(iii)
समीकरण (i), (ii) व (iii) के आधार पर ar (∆AOB) = ar (∆AOD) = ar (∆BOC) = ar (∆COD)
अर्थात् समान्तर चतुर्भुज के विकर्ण इसे समान क्षेत्रफल वाले चार त्रिभुजों में बाँटते हैं।
प्रश्न 4.
आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखण्ड CD रेखाखण्ड AB से बिन्दु O पर समद्विभाजित होता है, तो दर्शाइए कि ar (ABC) = ar (ABD) है।

हल-चित्र में दिए बिन्दु C से CM ⊥ AB तथा D बिन्दु से DN ⊥ AB खींचिए।
अब ∆CMO और ∆CNO में
∠CMO = ∠DNO (प्रत्येक 90°)
∠COM = ∠DON (शीर्षाभिमुख कोण)

तथा OC = OD
(क्योंकि O, CD का मध्य बिन्दु है)
अतः ∆CMO = ∆CNO
(सर्वांगसमता के नियम AAS के अनुसार)
अतः CM = DN …..(i) (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)
अब ar (∆ABC) = F × AB × CM …(ii)
ar (∆ADB) = 1 × AB × DN …(iii)
समीकरण (i) का मान (iii) में रखने पर ।
ar (∆ADB) = F × AB × CM….(iv)
अब समीकरण (ii) व (iv) से ar (∆ABC) = ar (∆ADB) (इति सिद्धम् )
प्रश्न 5.
D, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु हैं। दर्शाइए कि
(i) BDEF एक समान्तर चतुर्भुज है।
(ii) ar (DEF) = 1/4 ar (ABC)
(iii) ar (BDEF) = 1/2ar (ABC)
हल:
(i) प्रश्नानुसार बिन्दु F तथा E भुजा AB तथा भुजा AC के मध्य बिन्दु हैं। अतः
FE ∥ BC तथा FE = 1/2BC
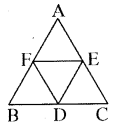
क्योंकि त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के समान्तर तथा उसका आधी होती है।
या FE ∥ BD
[क्योंकि BD, भुजा BC का ही भाग है।] तथा FE = BD
प्रश्नानुसार दिया है कि बिन्दु D भुजा BC का । मध्य बिन्दु है।
∴ BD = 1/2BC
अतः FE = 1/2BC
⇒ FE = BD
अब पुनः बिन्दु D तथा E क्रमश: BC तथा AC भुजाओं के मध्य-बिन्दु हैं। अतः
DE ∥ AB तथा DE = 1/2AB
या DE ∥ BF
[क्योंकि BF भुजा AB का ही भाग है] और DE = BF
∴ बिन्दु F, भुजा AB का मध्य-बिन्दु है अतः
BF = 1/2AB
परन्तु DE = AB
अत: DE = BF
अब FE ∥ BD तथा DE ∥ BF
या FE = BD तथा DE = BF
अत: BDEF एक समान्तर चतुर्भुज है।
(ii) ∵ BDEF एक समान्तर चतुर्भुज है, अतः ar (∆BDF) = ar (∆DEF). ……..(i)
[क्योंकि समान्तर चतुर्भुज का विकर्ण इसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करता है।]
DCEF भी एक समान्तर चतुर्भुज है,
अतः ar (∆DEF) = ar (∆DEC) …..(ii)
AEDF भी एक समान्तर चतुर्भुज है,
अतः ar (∆AFE) = ar (∆DEF) …..(iii)
समीकरण (i), (ii) व (iii) से ar (∆DEF) = ar (∆BDF) = ar (∆DEC) = ar (∆AFE)…..(iv)
अब ar (∆ABC) = ar (∆AFE) + ar (∆BDF) + ar (∆DEC) + ar (∆DEF) …..(v)
समीकरण (iv) का प्रयोग (v) में करने पर
या ar (∆ABC) = ar (∆DEF) + ar (∆DEF) + ar (∆DEF) + ar (∆DEF)
या ar (∆ABC) = 4 ar (∆DEF)
या 4 ar (∆DEF) = ar (∆ABC)
या ar (∆DEF) = 1/4ar (∆ABC)…(vi)
(iii) ar (समान्तर चतुर्भुज BDEF)
= ar (∆BDF) + ar (∆DEF) = ar (∆DEF) + ar (∆DEF) [समीकरण (iv) से]
= 2 ar (∆DEF) = 2 × 1/4ar (∆ABC)
[समीकरण (vi) से] अर्थात् ar (समान्तर चतुर्भुज BDEF = 1/2ar (∆ABC)
प्रश्न 6.
आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है, तो दर्शाइए कि

(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA ∥ CB या ABCD एक समान्तर
चतुर्भुज है। [संकेत : D और B से AC पर लम्ब खींचिए।]
हल:
(i) दिए गए चित्र में बिन्दु B से लम्ब BM ⊥ AC तथा बिन्दु D से लम्ब DN ⊥ AC खींचिए।

अब ∆DON और ∆BOM में
OD = OB (प्रश्नानुसार)
∠DNO = ∠BMO (प्रत्येक 90°)
तथा ∠DON = ∠BON(शीर्षाभिमुख कोण)
अतः ∆DON = ∆BOM
(सर्वांगसमता के नियम AAS के अनुसार)
अतः DN = BM (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)
तथा ar (∆DON) = ar (∆BOM) …..(i)
अब ∆DCN और ∆ABM में
∠DNC = ∠BMA (क्योंकि प्रत्येक कोण 90°)
CD = AB (प्रश्नानुसार)
तथा DN = BM (सिद्ध कर चुके हैं)
∆DCN ≅ ∆BAM
(सर्वांगसमता के नियम RHS के अनुसार)
अतः ar (∆DCN) = ar (∆BAM) …..(ii)
समीकरण (i) व (ii) को जोड़ने पर ar (∆DON) + ar (∆DCN) = ar (∆BOM) + ar (∆BAM)
या ar (∆DOC) = ar (∆AOB) …..(iii)
(ii) समीकरण (iii) के अनुसार
ar (∆DOC) = ar (∆AOB)
दोनों पक्षों में ar (∆BOC) जोड़ने पर ar (∆DOC) + ar (∆BOC) = ar (∆AOB) + ar (∆BOC)
या ar (∆DCB) = ar (∆ ACB) …..(iv)
(iii) समीकरण (iv) के अनुसार
ar (∆DCB) = ar (∆ACB) अर्थात् इन दोनों त्रिभुजों का आधार एक ही CB है तथा दोनों एक ही समान्तर रेखाओं CB तथा DA के बीच स्थित हैं।
अत: DA ∥ CB
अब AB = CD तथा DA ∥ CB अत: ABCD एक समान्तर चतुर्भुज है।।
प्रश्न 7.
बिन्दु D और E क्रमशः ∆ABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि ar (DBC) = ar (EBC) है। दर्शाइए कि DE ∥ BC है।
हल:
प्रश्नानुसार दिया गया है कि
ar (∆DBC) = ar (∆EBC)
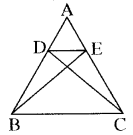
क्योंकि दो बराबर क्षेत्रफल वाले त्रिभुजों का | आधार एक ही BC है।
अतः DE ∥ BC
क्योंकि कोई भी दो त्रिभुज जिनका आधार तथा क्षेत्रफल बराबर या समान होता है, एक ही समान्तर रेखाओं के बीच स्थित होते हैं।
प्रश्न 8.
XY त्रिभुज ABC की भुजा BC के समान्तर एक रेखा है। यदि BE ∥ AC और CF ∥ AB रेखा XY से क्रमश: E और F पर मिलती हैं, तो दर्शाइए कि-ar (ABE) = ar (ACF)
हल:
चित्रानुसार क्योंकि ∆ABE तथा समान्तर चतुर्भुज BCYE एक ही आधार BE तथा एक ही समान्तर रेखाओं BE तथा AC के बीच स्थित हैं। अतः

ar (∆ABE) = 1/2ar (समान्तर चतुर्भुज BCYE)…..(i)
इसी प्रकार ∆ACF और समान्तर चतुर्भुज BCFX एक ही आधार CF तथा एक ही समान्तर रेखाओं BX और CF के बीच स्थित हैं। अतः
ar (∆ACF) = 1/2ar (समान्तर चतुर्भुज BCFX)…..(ii)
लेकिन समान्तर चतुर्भुज BCYE और समान्तर चतुर्भुज BCFX एक ही आधार BC और एक ही समान्तर रेखाओं BC और EF के बीच स्थित हैं।
अतः ar (समान्तर चतुर्भुज BCYE) = ar (समान्तर चतुर्भुज) BCFX) …..(iii)
समीकरण (i), (ii) व (iii) से
ar (∆ABE) = ar (∆ACF)
प्रश्न 9.
समान्तर चतुर्भुज ABCD की एक भुजा AB को एक बिन्दु P तक बढ़ाया गया है।A से होकर CP के समान्तर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समान्तर चतुर्भुज PBOR को पूरा किया गया है ( देखिए आकृति)। दर्शाइए कि ar (ABCD) = ar (PBQR) है।

[संकेत : AC और PQ को मिलाइए। अब ar (ACQ) और ar (APQ) की तुलना कीजिए।]
हल:
प्रश्नानुसार दिया गया है कि ABCD और PBQR समान्तर चतुर्भुज हैं तथा CP ∥ AQ।
अब क्योंकि ∆ACQ और ∆APQ एक ही आधार AQ तथा एक ही समान्तर रेखाओं AQ और CP के बीच स्थित हैं।
अतः ar (∆ACQ) = ar (∆APQ)
दोनों पक्षों में से ar (∆ABQ) घटाने पर ar (∆ACQ) – ar (∆ABQ) = ar (∆APQ) – ar (∆ABQ)
या ar (∆ACB) = ar (∆PBQ)
या 1212ar (समान्तर चतुर्भुज ABCD) = 1/2ar (समान्तर चतुर्भुज PBQR)
क्योंकि हम जानते हैं कि विकर्ण चतुर्भुज को बराबर क्षेत्रफल वाले त्रिभुजों में विभाजित करता है। अर्थात् त्रिभुज का क्षेत्रफल = 1/2 × समान्तर चतुर्भुज का क्षेत्रफल
अर्थात् ar (समान्तर चतुर्भुज ABCD) = ar (समान्तर चतुर्भुज PBQR)
प्रश्न 10.
एक समलम्ब ABCD, जिसमें AB ∥ DC है, के विकर्ण AC और BD परस्पर 0 पर प्रतिच्छेद करते हैं। दर्शाइए कि ar (AOD) = ar (BOC) है।
हल:
प्रश्नानुसार एवं चित्रानुसार अवलोकन करने पर हम देखते हैं कि ∆ABD और ∆ABC एक ही आधार AB और एक ही समान्तर रेखाओं AB तथा DC के बीच स्थित हैं।

अतः ar (∆ABD) = ar (∆ABC)
उपर्युक्त दोनों पक्षों में से ar (∆AOB) को घटाने पर ar (∆ABD) – ar (∆AOB) = ar (∆ABC) – ar (∆AOB)
या ar (∆AOD) = ar (∆BOC)
प्रश्न 11.
आकृति में, ABCDE एक पंचभुज है। B से होकर AC के समान्तर खींची गई रेखा बढ़ाई गई। DC को F पर मिलती है। दर्शाइए कि
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)

हल:
(i) प्रश्नानुसार दिया गया है कि BF ∥ AC तथा ∆ACB और ∆ACF एक ही आधार AC तथा एक ही समान्तर रेखाओं AC तथा BF के बीच स्थित हैं। अतः
ar (∆ACB) = ar (∆ACF) …..(1)
(ii) अब ar (ABCDE) = ar (समलम्ब चतुर्भुज AEDC) + ar (∆ABC) …..(2)
समीकरण (1) का प्रयोग (2) में करने पर
ar (ABCDE) = ar (समलम्ब चतुर्भुज AEDC) + ar (∆ACF) = ar (समलम्ब चतुर्भुज AEDC) + ar (∆ACF)
= ar (चतुर्भुज AEDF)
या ar (AEDF) = ar (ABCDE)
प्रश्न 12.
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केन्द्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध के साथ स्वीकार कर लेता है कि इसे इस भाग के बदले उसी भूखंड के संलग्न एक भाग ऐसा दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
हल:
माना कि इतवारी के पास PQRS एक चतुर्भुजाकार भूखण्ड था। भुजा PQ को T बिन्दु तक बढ़ाइए। QS को मिलाइए तथा RT ∥ QS खींची।

चित्रानुसार क्योंकि ∆QSR और ∆QST एक ही आधार QS तथा एक ही समान्तर रेखाओं QS तथा RT के बीच स्थित हैं
अतः ar (∆QSR) = ar (∆QST)
उपर्युक्त में दोनों ओर ar (∆PQS) जोड़ने पर ar (∆PQS) + ar (∆QSR) = ar (∆PQS) + ar (∆QST)
या ar (PQRS) = ar (∆PTS)
अतः स्वास्थ्य केन्द्र के लिए दिया गया भूखण्ड = ar (∆RSO)
उक्त भूखण्ड के बदले इतवारी को मिला भूखण्ड = ar (∆QTO)
प्रश्न 13.
ABCD एक समलम्ब है, जिसमें AB ∥ DC है। AC के समान्तर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ar (ADX) = ar (ACY) है।
[संकेत : CX को मिलाइए।]
हल:
प्रश्नानुसार एवं चित्रानुसार CX को मिलाया। अब ∆ADX और ∆ACX एक ही आधार XA पर तथा एक ही समान्तर रेखाओं AB और DC के बीच स्थित हैं। अतः
ar (∆ADX) = ar (∆ACX) …..(i)
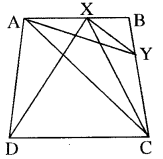
साथ ही ∆ACX तथा ∆ACY एक ही आधार AC तथा एक ही समान्तर रेखाओं AC और XY के बीच स्थित है।
अतः ar (∆ACX) = ar (∆ACY) …..(ii)
समीकरण () व (ii) से ar (∆ADX) = ar (∆ACY) (इति सिद्धम्)
प्रश्न 14.
आकृति में, AP ∥ BQ ∥ CR है। सिद्ध कीजिए कि ar (AQC) = ar (PBR) है।

हल:
चित्रानुसार हम देख सकते हैं कि ∆ABQ और ∆BPQ एक ही आधार BQ तथा एक ही समान्तर रेखाओं AP तथा BQ के बीच स्थित हैं।
अतः ar (∆ABQ) = ar (∆BPQ) …..(i)
इसी प्रकार ∆BQC और ∆BQR एक ही आधार BQ तथा एक ही समान्तर रेखाओं BQ तथा CR के बीच स्थित हैं। अतः
ar (∆BQC) = ar (∆BQR) …..(ii)
समीकरण (i) व (ii) को जोड़ने पर। ar (∆ABQ) + ar (∆BQC) = ar (∆BPQ) + ar (∆BQR)
या ar (∆AQC) = ar (∆PBR) (इति सिद्धम्)
प्रश्न 15.
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु 0 पर इस प्रकार प्रतिच्छेद करते हैं कि ar (AOD) = ar (BOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब है।
हल:
प्रश्नानुसार दिया गया है कि
ar (D AOD) = ar (D BOC) …..(i)
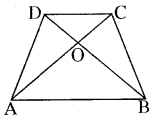
समीकरण (i) के दोनों पक्षों में ar (∆AOB) जोड़ने पर ar (∆AOD) + ar (∆AOB) = ar (∆BOC) + ar (∆AOB)
या ar (∆ABD) = ar (∆ABC)
क्योंकि हम जानते हैं कि यदि कोई दो त्रिभुज समान क्षेत्रफल तथा एक ही आधार पर स्थित हों, तो वे एक ही समान्तर रेखाओं के बीच स्थित होते हैं।
चित्रानुसार ∆ABD और ∆ABC एक ही आधार AB पर स्थित हैं और इनके क्षेत्रफल भी समान हैं अतः ये एक ही समान्तर रेखाओं AB और DC के बीच स्थित हैं।
अर्थात् AB ∥ DC
अब चतुर्भुज ABCD में AB ∥ DC
अत: ABCD एक समलम्ब चतुर्भुज है क्योंकि | समलम्ब में सम्मुख भुजाओं का एक युग्म समान्तर होता है।
प्रश्न 16.
आकृति में ar (DRC) = ar (DPC) है और ar (BDP) = ar (ARC) है। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलम्ब हैं।

हल:
प्रश्नानुसार दिया गया है कि ∆DRC तथा ∆DPC एक ही आधार DC पर स्थित हैं
तथा ar (∆DRC) = ar (∆DPC) …..(i)
अतः DC ∥ RP क्योंकि हम जानते हैं कि समान क्षेत्रफल वाले दो त्रिभुज एक ही आधार पर स्थित हों तो वे सदैव ही समान्तर रेखाओं के बीच स्थित होते हैं।
अब चतुर्भुज DCPR में DC ∥ RP
अत: DCRP एक समलम्ब चतुर्भुज है। साथ ही यह भी दिया गया है कि
ar (∆BDP) = ar (∆ARC) …..(ii)
समीकरण (i) को इस प्रकार भी लिखा जा सकता
ar (∆DPC) = ar (∆DRC) …..(iii)
समीकरण (iii) को समीकरण (ii) में से घटाने पर ar (∆BDP) – ar (∆DPC) = ar (∆ARC) – ar (∆DRC)
या ar (∆BDC) = ar (∆ADC).
चूँकि हम जानते हैं कि यदि समान क्षेत्रफल वाले दो त्रिभुज एक ही आधार पर स्थित हों तो वे सदैव एक ही समान्तर रेखाओं के बीच स्थित होते हैं ।
यहाँ इस प्रश्न में भी ∆BDC
तथा ∆ADC समान क्षेत्रफल के तथा एक ही आधार पर स्थित हैं DC पर अतः AB ∥ DC
अब चतुर्भुज ABCD में AB ∥ DC
अत: ABCD एक समलम्ब है।